6.3: Guía de ondas de placa paralela - Caja TE, campo eléctrico

En la Sección 6.2 se introdujo la guía de ondas de placa paralela. Al final de esa sección describimos la descomposición del problema en sus componentes TE y TM. En esta sección, encontramos el componente de campo eléctrico del campo TE en la guía de ondas.

En la figura se\(\PageIndex{1}\) muestra el problema abordado en esta sección. (Los detalles y supuestos adicionales se abordan en la Sección 6.2.)

Figura\(\PageIndex{1}\): Componente TE del campo eléctrico en una guía de ondas de placa paralela. (CC BY-SA 4.0; C. Wang)

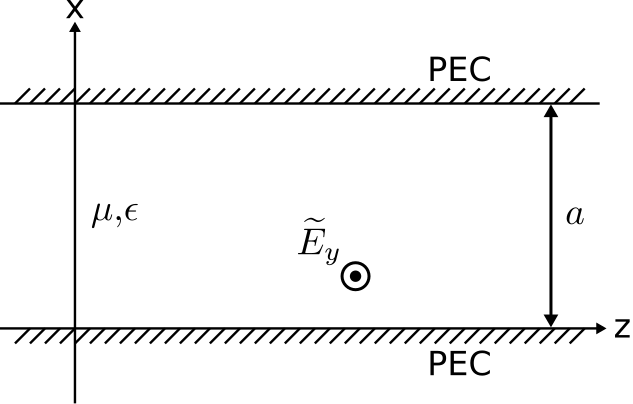
Ya que\(\widetilde{E}_x=\widetilde{E}_z=0\) para el componente TE del campo eléctrico, las Ecuaciones 6.2.11 y 6.2.13 son irrelevantes, dejando solo:

\[\frac{\partial^2}{\partial x^2}\widetilde{E}_y + \frac{\partial^2}{\partial z^2}\widetilde{E}_y = - \beta^2 \widetilde{E}_y \label{m0174_eDE} \]

La solución general a esta ecuación diferencial parcial es:

\[\begin{align} \widetilde{E}_y =&~~~~~e^{-jk_z z} \left[ A e^{-jk_x x} + B e^{+jk_x x} \right] \nonumber \\ &+e^{+jk_z z} \left[ C e^{-jk_x x} + D e^{+jk_x x} \right] \label{m0174_eGS}\end{align} \]

donde\(A\),\(B\)\(C\), y\(D\) son constantes de valor complejo y\(k_x\) y\(k_z\) son constantes de valor real. Hemos asignado nombres de variables a estas constantes con conocimiento avanzado de su interpretación física; sin embargo, en este momento siguen siendo constantes simplemente desconocidas cuyos valores deben ser determinados por la aplicación de condiciones límite.

Tenga en cuenta que la Ecuación\ ref {M0174_EGS} consta de dos términos. El primer término incluye el factor\(e^{-jk_z z}\), indicando una onda que se propaga en la\(+\hat{\bf z}\) dirección, y el segundo término incluye el factor\(e^{+jk_z z}\), indicando una onda que se propaga en la\(-\hat{\bf z}\) dirección. Si imponemos la restricción de que las fuentes existen solo en el lado izquierdo (\(z<0\)) de la Figura\(\PageIndex{1}\), y que no hay ninguna estructura capaz de dispersar la onda (en particular, reflexión) en el lado derecho (\(z>0\)) de la Figura\(\PageIndex{1}\), entonces no puede haber componentes de onda que se propaguen en el \(-\hat{\bf z}\)dirección. En este caso,\(C=D=0\) y la Ecuación\ ref {M0174_EGs} simplifica a:

\[\widetilde{E}_y = e^{-jk_z z} \left[ A e^{-jk_x x} + B e^{+jk_x x} \right] \label{m0174_eGS2} \]

Antes de continuar, asegurémonos de que la Ecuación\ ref {M0174_EGS2} es en realidad una solución a la Ecuación\ ref {M0174_ede}. Como veremos en un momento, realizar esta comprobación revelará alguna información útil adicional. Primero, tenga en cuenta:

\[\frac{\partial \widetilde{E}_y}{\partial x} = e^{-jk_z z} \left[-A e^{-jk_x x} + B e^{+jk_x x} \right]\left(jk_x\right) \nonumber \]

Entonces:

\[\frac{\partial^2 \widetilde{E}_y}{\partial x^2} = e^{-jk_z z} \left[ A e^{-jk_x x} + B e^{+jk_x x} \right]\left(-k_x^2\right) \nonumber \]

Comparando esto con la Ecuación\ ref {M0174_EGS2}, observamos el hecho notable de que

\[\frac{\partial^2 \widetilde{E}_y}{\partial x^2} = -k_x^2 \widetilde{E}_y \nonumber \]

Asimismo, tenga en cuenta:

\[\frac{\partial \widetilde{E}_y}{\partial z} = e^{-jk_z z} \left[ A e^{-jk_x x} + B e^{+jk_x x} \right]\left(-jk_z\right) \nonumber \]

Entonces:

\[\begin{align} \frac{\partial^2 \widetilde{E}_y}{\partial z^2} &= e^{-jk_z z} \left[ A e^{-jk_x x} + B e^{+jk_x x} \right]\left(-k_z^2\right) \nonumber \\ &= -k_z^2 \widetilde{E}_y\end{align} \nonumber \]

Ahora sumando estos resultados:

\[\frac{\partial^2 \widetilde{E}_y}{\partial x^2} + \frac{\partial^2 \widetilde{E}_y}{\partial z^2} = -\left( k_x^2 + k_z^2 \right) \widetilde{E}_y \label{m0174_eDE2} \]

Comparando la Ecuación\ ref {M0174_EDe2} con la Ecuación\ ref {M0174_Ede}, concluimos que la Ecuación\ ref {M0174_EGS2} es de hecho una solución a la Ecuación\ ref {M0174_ede}, pero solo si:

\[\beta^2 = k_x^2 + k_z^2 \label{m0174_eBeta} \]

Esto confirma que\(k_x\) y\(k_z\) son de hecho los componentes del vector de propagación

\[{\bf k} \triangleq \beta\hat{\bf k} = \hat{\bf x}k_x + \hat{\bf y}k_y + \hat{\bf z}k_z \nonumber \]

dónde\(\hat{\bf k}\) está el vector unitario apuntando en la dirección de propagación, y\(k_y=0\) en este problema particular.

La solución ahora se ha reducido a encontrar las constantes\(A\),\(B\), y cualquiera\(k_x\) o\(k_z\). Esto se logra mediante el cumplimiento de las condiciones de frontera relevantes. En general, el componente de\(\widetilde{\bf E}\) eso es tangente a una superficie perfectamente conductora es cero. Aplicado al problema actual, esto significa\(\widetilde{E}_y = 0\) en\(x=0\) y\(\widetilde{E}_y = 0\) en\(x=a\). Refiriéndose a la Ecuación\ ref {M0174_EGS2}, la condición de límite en\(x=0\) medias

\[e^{-jk_z z} \left[ A \cdot 1 + B \cdot 1 \right] = 0 \nonumber \]

El factor\(e^{-jk_z z}\) no puede ser cero; por lo tanto,\(A+B=0\). Ya que\(B=-A\), podemos reescribir la ecuación\ ref {m0174_EGS2} de la siguiente manera:

\[\widetilde{E}_y = e^{-jk_z z} B \left[ e^{+jk_x x} - e^{-jk_x x} \right] \nonumber \]

Esta expresión se simplifica usando una identidad trigonométrica:

\[\frac{1}{2j}\left[ e^{+jk_x x} - e^{-jk_x x} \right] = \sin{k_x x} \nonumber \]

Hagamos ahora la definición\(E_{y0}\triangleq j2B\). Entonces:

\[\widetilde{E}_y = E_{y0} e^{-jk_z z} \sin k_x x \label{m0174_eGS3} \]

Ahora aplicando la condición de contorno en\(x=a\):

\[E_{y0} e^{-jk_z z} \sin k_x a = 0 \nonumber \]

El factor\(e^{-jk_z z}\) no puede ser cero, y solo\(E_{y0}=0\) arroja soluciones triviales; por lo tanto:

\[\sin{k_x a} = 0 \nonumber \]

Esto a su vez requiere que

\[k_x a = m \pi \label{m0174_ekxa} \]

donde\(m\) es un número entero. Obsérvese que no\(m=0\) es de interés ya que esto rinde\(k_x=0\), que de acuerdo con la Ecuación\ ref {M0174_EGS3} rinde la solución trivial\(\widetilde{E}_y=0\). También se excluye cada valor entero de\(m\) que sea menor que cero porque la solución asociada es diferente de la solución para el valor positivo correspondiente de solo\(m\) en signo, que puede ser absorbido en la constante arbitraria\(E_{y0}\).

En este punto hemos descubierto una familia de soluciones dadas por la Ecuación\ ref {M0174_EGS3} y la Ecuación\ ref {m0174_ekxa} con\(m=1,2,...\). Cada solución asociada con un valor particular de\(m\) se conoce como un modo, que (a través de la ecuación\ ref {m0174_ekxa}) tiene un valor particular de\(k_x\). El valor de\(k_z\) for mode\(m\) se obtiene usando la ecuación\ ref {M0174_Ebeta} de la siguiente manera:

\[\begin{align} k_z &= \sqrt{\beta^2-k_x^2} \nonumber \\ & =\sqrt{\beta^2-\left(\frac{m\pi}{a}\right)^2}\end{align} \nonumber \]

Dado que\(k_z\) se especifica para ser de valor real, requerimos:

\[\beta^2-\left(\frac{m\pi}{a}\right)^2 > 0 \nonumber \]

Esto constriñe\(\beta\); específicamente:

\[\beta > \frac{m\pi}{a} \nonumber \]

Recordemos eso\(\beta=\omega\sqrt{\mu\epsilon}\) y\(\omega=2\pi f\) dónde\(f\) está la frecuencia. Resolviendo para\(f\), encontramos:

\[f > \frac{m}{2a\sqrt{\mu\epsilon}} \nonumber \]

Por lo tanto, cada modo existe solo por encima de una cierta frecuencia, que es diferente para cada modo. Esta frecuencia de corte\(f_c\) para el modo\(m\) viene dada por

\[\boxed{ f_c^{(m)} \triangleq \frac{m}{2a\sqrt{\mu\epsilon}} } \label{m0174_efcm} \]

A frecuencias por debajo de la frecuencia de corte para el modo\(m\), los modos\(1\) a través de\(m-1\) exhiben valores imaginarios\(k_z\). La constante de propagación debe tener un componente de valor real para poder propagarse; por lo tanto, estos modos no se propagan y pueden ser ignorados.

Resumamos ahora la solución. Para el escenario representado en la Figura\(\PageIndex{1}\), el componente de campo eléctrico de la solución TE viene dado por:

\[\boxed{ \hat{\bf y}\widetilde{E}_y = \hat{\bf y}\sum_{m=1}^{\infty} \widetilde{E}_y^{(m)} } \label{m0174_eEysum} \]

donde

\[\boxed{ \widetilde{E}_y^{(m)} \triangleq \begin{cases} 0, & f<f_c^{(m)} \\ E_{y0}^{(m)} e^{-jk_z^{(m)} z} \sin k_x^{(m)} x, & f\ge f_c^{(m)} \end{cases} } \nonumber \]

donde\(m\) enumera los modos (\(m=1,2,...\)),

\[\boxed{ k_z^{(m)} \triangleq \sqrt{\beta^2-\left[k_x^{(m)}\right]^2} } \nonumber \]

y

\[\boxed{ k_x^{(m)} \triangleq m\pi/a } \label{m0174_ekxma} \]

Finalmente,\(E_{y0}^{(m)}\) es una constante de valor complejo que depende de fuentes o condiciones de límite a la izquierda de la región de interés.

Para el escenario representado en la Figura\(\PageIndex{1}\), el componente de campo eléctrico de la solución TE viene dado por la Ecuación\ ref {M0174_EEYSUM} con componentes modales determinados como se indica por Ecuaciones\ ref {m0174_efcm} -\ ref {m0174_ekxma}. Esta solución presume que todas las fuentes se encuentran a la izquierda de la región de interés, y no se produce dispersión alguna a la derecha de la región de interés.

Para entender mejor este resultado, examinemos el modo de orden más bajo,\(m=1\). Para este modo\(f_c^{(1)}=1/2a\sqrt{\mu\epsilon}\), por lo que este modo puede existir si\(f>1/2a\sqrt{\mu\epsilon}\). También\(k_x^{(1)} = \pi/a\), por lo

\[k_z^{(1)} = \sqrt{\beta^2-\left(\frac{\pi}{a}\right)^2} \label{m0174_ekz1} \]

Posteriormente,

\[\widetilde{E}_y^{(1)} = E_{y0}^{(1)} e^{-jk_z^{(1)} z} \sin \frac{\pi x}{a} \nonumber \]

Tenga en cuenta que este modo tiene la forma de una onda plana. La onda plana se propaga en la\(+\hat{\bf z}\) dirección con constante de propagación de fase\(k_z^{(1)}\). Además, observamos que la onda plana aparente no es uniforme, exhibiendo una magnitud proporcional al\(\sin \pi x/a\) interior de la guía de ondas. Esto se muestra en la Figura\(\PageIndex{2}\) (imagen izquierda).

Figura\(\PageIndex{2}\): Magnitud de los dos modos TE de menor orden en una guía de ondas de placa paralela. Izquierda:\(m=1\), Derecha:\(m=2\). (CC BY-SA 4.0; C. Wang)

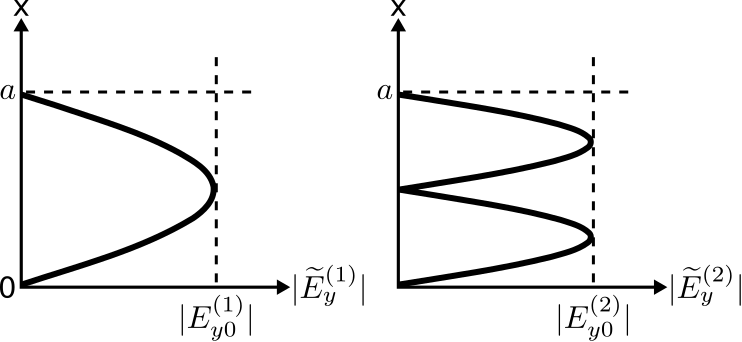
En particular, observamos que la magnitud de la onda es cero en las superficies de conducción perfecta —como es necesario para satisfacer las condiciones límite— y es máxima en el centro de la guía de ondas.

Ahora examinemos el\(m=2\) modo. Para este modo,\(f_c^{(2)}=1/a\sqrt{\mu\epsilon}\), por lo que este modo puede existir si\(f>1/a\sqrt{\mu\epsilon}\). Esta frecuencia es mayor que\(f_c^{(1)}\), por lo que el\(m=1\) modo puede existir en cualquier frecuencia en la que exista el\(m=2\) modo. También\(k_x^{(2)} = 2\pi/a\), por lo

\[k_z^{(2)} = \sqrt{\beta^2-\left(\frac{2\pi}{a}\right)^2} \label{m0174_ekz2} \]

Posteriormente,

\[\widetilde{E}_y^{(2)} = E_{y0}^{(2)} e^{-jk_z^{(2)} z} \sin \frac{2\pi x}{a} \nonumber \]

En este caso, la onda plana aparente se propaga en la\(+\hat{\bf z}\) dirección con constante de propagación de fase\(k_z^{(2)}\), que es menor que\(k_z^{(1)}\). Porque\(m=2\), encontramos que la magnitud es proporcional al\(\sin 2\pi x/a\) interior de la guía de ondas (Figura\(\PageIndex{2}\), imagen derecha). Como en el\(m=1\) caso, observamos que la magnitud de la onda es cero en las superficies PEC; sin embargo\(m=2\), para, hay dos máximos con respecto a\(x\), y la magnitud en el centro de la guía de ondas es cero.

Este patrón continúa para los modos de orden superior. En particular, cada modo sucesivo exhibe una frecuencia de corte más alta, una constante de propagación más pequeña y un número entero creciente de semiperiodos sinusoidales en magnitud.

Ejemplo\(\PageIndex{1}\): Single-mode TE propagation in a parallel plate waveguide

Considere una guía de ondas de placa paralela llena de aire que consiste en placas separadas por\(1\) cm. Determinar el rango de frecuencia para el cual se asegura uno (y solo uno) que se propaga el modo TE.

Solución

La propagación TE monomodo se asegura limitando la frecuencia\(f\) a mayor que la frecuencia de corte para\(m=1\), pero menor que la frecuencia de corte para\(m=2\). (Cualquier frecuencia mayor que la frecuencia de corte\(m=2\) permite que existan al menos 2 modos). Calculando las frecuencias de corte aplicables, encontramos:

\[\begin{aligned} f_c^{(1)} &= \frac{1}{2a\sqrt{\mu_0\epsilon_0}} \cong 15.0 \: ~\mbox{GHz} \\ f_c^{(2)} &= \frac{2}{2a\sqrt{\mu_0\epsilon_0}} \cong 30.0 \:~\mbox{GHz} \end{aligned} \nonumber \]

Por lo tanto,\(15.0 \: \mathrm{GHz} \leq f \leq 30.0 \: \mathrm{GHz}\).

Finalmente, consideremos la velocidad de fase\(v_p\) dentro de la guía de ondas. Para el modo de orden más bajo\(m=1\), esto es

\[v_p = \frac{\omega}{k_z^{(1)}} = \frac{\omega}{\sqrt{\omega^2\mu\epsilon-\left(\frac{\pi}{a}\right)^2}} \label{m0174_evp} \]

Recordemos que la velocidad de una onda electromagnética en un espacio ilimitado (es decir, no en una guía de ondas) es\(1/\sqrt{\mu\epsilon}\). Por ejemplo, la velocidad de la luz en el espacio libre es\(1/\sqrt{\mu_0\epsilon_0}=c\). Sin embargo, la velocidad de fase indicada por la Ecuación\ ref {m0174_evp} es mayor que\(1/\sqrt{\mu\epsilon}\); por ejemplo, más rápida de lo que la luz viajaría en el mismo material (presumiendo que era transparente). A primera vista, esto puede parecer imposible. Sin embargo, recuerde que la información viaja a la velocidad del grupo\(v_g\), y no necesariamente a la velocidad de fase. (Ver Sección 6.1 para un repaso.) Aunque no lo demostraremos aquí, la velocidad de grupo en la guía de ondas de placa paralela es siempre menor que\(1/\sqrt{\mu\epsilon}\), por lo que no se rompen las leyes físicas, y las señales viajan algo más despacio que la velocidad de la luz, como lo hacen en cualquier otra estructura utilizada para transmitir señales.

También es notable que la velocidad de propagación es diferente para cada modo. De hecho, encontramos que la velocidad de fase aumenta y la velocidad del grupo disminuye a medida que\(m\) aumenta. Este fenómeno se conoce como dispersión, y algunas veces específicamente como dispersión de modo o dispersión modal.