7.3: Atenuación en Cable Coaxial
- Page ID
- 83646
En esta sección, consideramos el tema de la atenuación en línea de transmisión coaxial. Recordemos que la atenuación puede interpretarse en el contexto del modelo de línea de transmisión de circuito equivalente “elemento agrupado” como las contribuciones de la resistencia por unidad de longitud\(R'\) y conductancia por unidad de longitud\(G'\). En este modelo,\(R'\) representa la resistencia física en los conductores internos y externos, mientras que\(G'\) representa la pérdida debida a la corriente que fluye directamente entre los conductores a través del material espaciador.
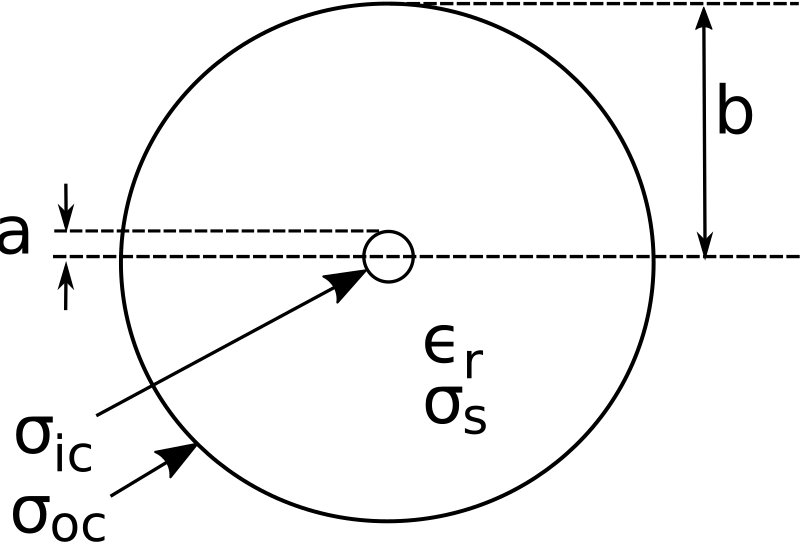
Los parámetros utilizados para describir las características relevantes del cable coaxial se muestran en la Figura\(\PageIndex{1}\). En esta figura,\(a\) y\(b\) están los radios de los conductores interno y externo, respectivamente. \(\sigma_{ic}\)y\(\sigma_{oc}\) son las conductividades (unidades base SI de S/m) de los conductores internos y externos, respectivamente. Se supone que los conductores no son magnéticos; es decir, que tienen permeabilidad\(\mu\) igual al valor del espacio libre\(\mu_0\). Se supone que el material espaciador es un dieléctrico con pérdidas que tiene permitividad\(\epsilon_r\) y conductividad relativas\(\sigma_s\).
Resistencia por unidad de longitud
La resistencia por unidad de longitud es la suma de las resistencias del conductor interno y externo por unidad de longitud. La resistencia por unidad de longitud del conductor interno está determinada por\(\sigma_{ic}\) y el área de sección transversal efectiva a través de la cual fluye la corriente. Este último es igual a la circunferencia\(2\pi a\) por la profundidad\(\delta_{ic}\) de la piel del conductor interno, por lo que:
\[R_{ic}' \approx \frac{1}{\left(2\pi a \cdot \delta_{ic} \right) \sigma_{ic} } ~~~ \mbox{for} ~ \delta_{ic} \ll a \nonumber \]
Esta expresión solo es válida\(\delta_{ic} \ll a\) porque de lo contrario el área de la sección transversal a través de la cual fluye la corriente no está bien modelada como un anillo delgado cerca de la superficie del conductor. Del mismo modo, encontramos que la resistencia por unidad de longitud del conductor externo es
\[R_{oc}' \approx \frac{1}{\left(2\pi b \cdot \delta_{oc} \right) \sigma_{oc} } ~~~ \mbox{for} ~ \delta_{oc} \ll t \nonumber \]
donde\(\delta_{oc}\) es la profundidad de la piel del conductor externo y\(t\) es el grosor del conductor externo. Por lo tanto, la resistencia total por unidad de longitud es
\ begin {align} R' &= R_ {ic} '+ R_ {oc}'\ nonumber\\ &\ approx\ frac {1} {\ left (2\ pi a\ cdot\ delta_ {ic}\ derecha)\ sigma_ {ic}} +\ frac {1} {\ izquierda (2\ pi b\ cdot\ delta_ {oc}\ derecha)\ sigma_ {oc}}\ etiqueta {M0189_ERP1}\ end {align}
Recordemos que la profundidad de la piel depende de la conductividad. Específicamente:
\ begin {align}\ delta_ {ic} &=\ sqrt {2/\ omega\ mu\ sigma_ {ic}}\\ delta_ {oc} &=\ sqrt {2/\ omega\ mu\ sigma_ {oc}}\ end {align}
Expandiendo la Ecuación\ ref {M0189_ERP1} para mostrar explícitamente la dependencia de la conductividad, encontramos:
\[R' \approx \frac{1}{2\pi \sqrt{2/\omega\mu_0} } \left[ \frac{1}{a \sqrt{\sigma_{ic}} } + \frac{1}{b \sqrt{\sigma_{oc}} } \right] \nonumber \]
En este punto es conveniente identificar dos casos particulares para el diseño del cable. En el primer caso, “Caso I”, asumimos\(\sigma_{oc} \gg \sigma_{ic}\). Ya que\(b > a\), tenemos en este caso
\ begin {align} R' &\ approx\ frac {1} {2\ pi\ sqrt {2/\ omega\ mu_0}}\ izquierda [\ frac {1} {a\ sqrt {\ sigma_ {ic}}\ derecha]\ nonumber\\ &=\ frac {1} {2\ pi\ delta_ {ic}\ sigma_ {ic} ~\ frac {1} {a} ~~~\ mbox {(Caso~I)}\ end {align}
En el segundo caso, “Caso II”, asumimos\(\sigma_{oc} = \sigma_{ic}\). En este caso, tenemos
\ begin {align} R' &\ approx\ frac {1} {2\ pi\ sqrt {2/\ omega\ mu_0}}\ left [\ frac {1} {a\ sqrt {\ sigma_ {ic}}} +\ frac {1} {b\ sqrt {\ sigma_ {ic}}\ derecha]\ nonumber\\ &=\ frac {1} {2\ pi\ delta_ {ic}\ sigma_ {ic}} ~\ izquierda [\ frac {1} {a} +\ frac {1} {b}\ derecha] ~~~\ mbox {(Caso~II)}\ end {align}
Una forma más sencilla de tratar estos dos casos es representarlos a ambos usando la expresión única
\[R' \approx \frac{1}{2\pi \delta_{ic} \sigma_{ic} }~\left[ \frac{1}{a} + \frac{C}{b} \right] \nonumber \]
donde\(C=0\) en el Caso I y\(C=1\) en el Caso II.
Conductancia por unidad de longitud
La conductancia por unidad de longitud del cable coaxial es simplemente la de la estructura coaxial asociada a CC; es decir,
\[G' = \frac{2\pi\sigma_s}{\ln\left(b/a\right)} \nonumber \]
A diferencia de la resistencia, la conductancia es independiente de la frecuencia, al menos en la medida en que\(\sigma_s\) sea independiente de la frecuencia.
Atenuación
La atenuación de las ondas de voltaje y corriente a medida que se propagan a lo largo del cable está representada por el factor\(e^{-\alpha z}\), donde\(z\) se recorre la distancia a lo largo del cable. Es posible encontrar una expresión para\(\alpha\) en términos de los parámetros de material y geometría usando:
\[\gamma \triangleq \sqrt{ \left( R' + j\omega L' \right) \left( G' + j\omega C' \right)} = \alpha + j\beta \label{m0189_fGamma} \]
donde\(L'\) y\(C'\) son la inductancia por unidad de longitud y la capacitancia por unidad de longitud, respectivamente. Estos son dados por
\[L' = \frac{\mu}{2\pi}\ln{\left(b/a\right)} \nonumber \]
y
\[C' = \frac{2\pi\epsilon_0\epsilon_r}{\ln{\left(b/a\right)}} \nonumber \]
En principio podríamos resolver la Ecuación\ ref {M0189_Fgamma} para\(\alpha\). Sin embargo, este curso de acción es bastante tedioso, y un enfoque aproximado más simple facilita algunas ideas adicionales. En este enfoque, definimos parámetros\(\alpha_R\) asociados\(R'\) y\(\alpha_G\) asociados con\(G'\) tales que
\[e^{-\alpha_R z} e^{-\alpha_G z} = e^{-\left(\alpha_R+\alpha_G\right) z} = e^{-\alpha z} \nonumber \]
que indica
\[\alpha = \alpha_R + \alpha_G \nonumber \]
Siguiente postulamos
\[\alpha_R \approx K_R \frac{R'}{Z_0} \label{m0189_eAlphaR} \]
donde\(Z_0\) esta la impedancia característica
\[Z_0 \approx \frac{\eta_0}{2\pi}\frac{1}{\sqrt{\epsilon_r}}\ln{\frac{b}{a}}~~~\mbox{(low loss)} \label{m0189_eZ0cc} \]
y donde\(K_R\) hay una constante sin unidad por determinar. La justificación para la Ecuación\ ref {M0189_Ealphar} es la siguiente: Primero,\(\alpha_R\) debe aumentar monótonamente con el aumento\(R'\). Segundo,\(R'\) debe dividirse por una impedancia para obtener las unidades correctas de 1/m. Utilizando razonamiento similar, postulamos
\[\alpha_G \approx K_G G' Z_0 \label{m0189_eAlphaG} \]
donde\(K_G\) es una constante sin unidad por determinar. El siguiente ejemplo demuestra la validez de las Ecuaciones\ ref {M0189_Ealphar} y\ ref {M0189_EalphaG}, y revelará los valores de\(K_R\) y\(K_G\).
RG-59 es una forma popular de cable coaxial que tiene los parámetros\(a \cong 0.292~\) mm,\(b \cong 1.855\) mm,\(\sigma_{ic} \cong 2.28 \times 10^7\) S/m,\(\sigma_s \cong 5.9 \times 10^{-5}\) S/m, y\(\epsilon_r \cong 2.25\). La conductividad\(\sigma_{oc}\) del conductor externo es difícil de cuantificar porque consiste en una trenza de hebras metálicas delgadas. No obstante\(\sigma_{oc}\gg\sigma_{ic}\), así podemos asumir el Caso I; es decir,\(\sigma_{oc}\gg\sigma_{ic}\), y posteriormente\(C=0\).
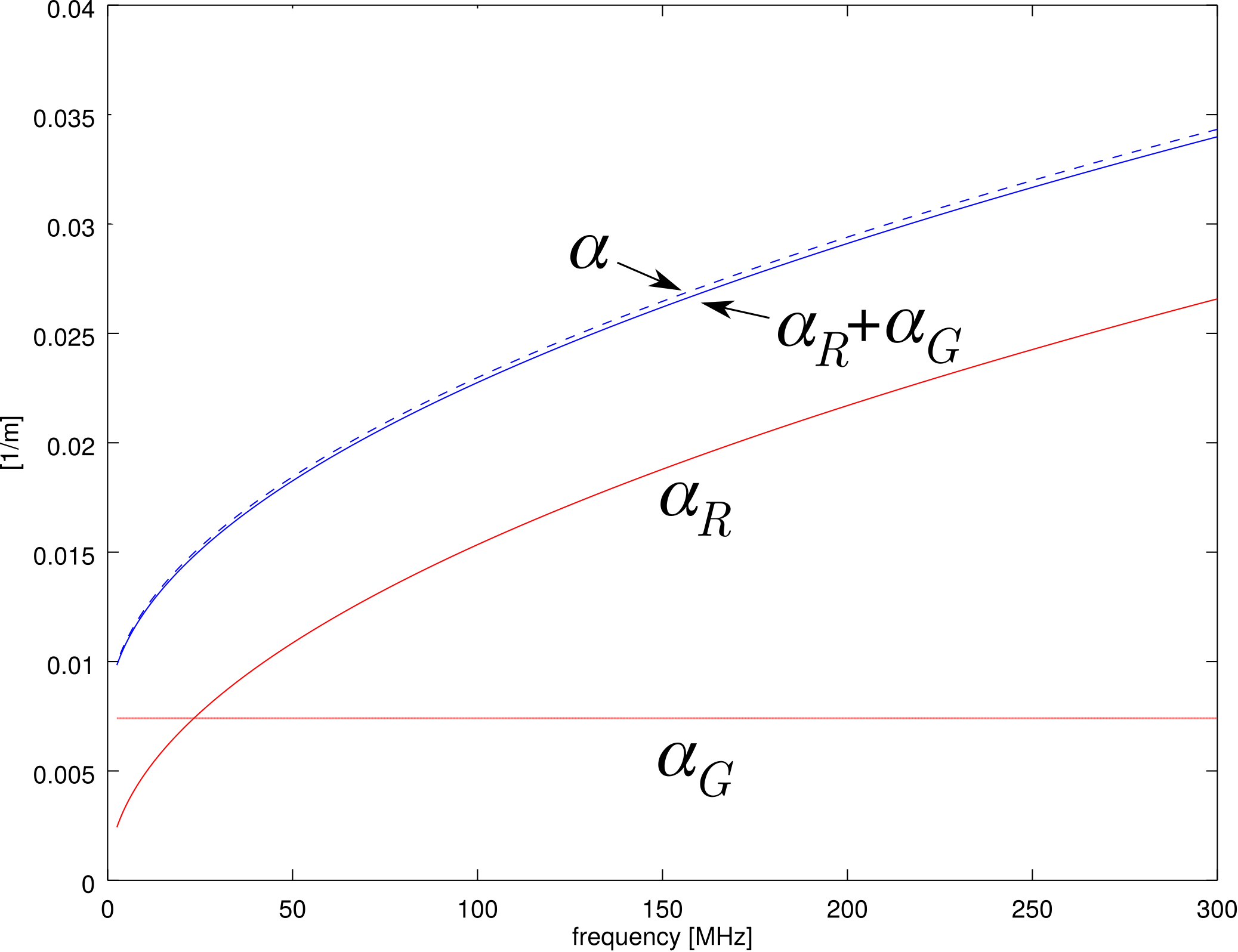
La figura\(\PageIndex{2}\) muestra los componentes\(\alpha_G\) y\(\alpha_R\) computados para la elección particular\(K_R=K_G=1/2\). La figura también muestra\(\alpha_G + \alpha_R\), junto con\(\alpha\) computado usando la ecuación\ ref {M0189_fgamma}. Encontramos que el acuerdo entre estos valores es muy bueno, lo que es evidencia convincente de que el ansatz es válido y\(K_R=K_G=1/2\).
Obsérvese que no hay nada que indique que los resultados demostrados en el ejemplo no son generalmente ciertos. Así, llegamos a la siguiente conclusión:
La constante de atenuación\(\alpha\approx\alpha_G+\alpha_R\) donde\(\alpha_G\triangleq R'/2Z_0\) y\(\alpha_R\triangleq G'Z_0/2\).
Minimizar la atenuación
Consideremos ahora si hay opciones de diseño que minimicen la atenuación del cable coaxial. Ya que\(\alpha=\alpha_R+\alpha_G\), podemos considerar\(\alpha_R\) e\(\alpha_G\) independientemente. Consideremos primero\(\alpha_G\):
\ begin {align}\ alpha_g &\ triangleq\ frac {1} {2} G'Z_0\ nonumber\\ &\ approx\ frac {1} {2}\ cdot\ frac {2\ pi\ sigma_s} {\ ln\ izquierda (b/a\ derecha)}\ cdot\ frac {1} {2\ pi}\ frac\ eta_0} {\ sqrt {\ epsilon_r}}\ ln\ izquierda (b/a\ derecha)\ nonumber\\ &=\ frac {\ eta_0} {2} ~\ frac {\ sigma_s} {\ sqrt {\ epsilon_r}}\ end {align}
De este resultado queda claro que\(\alpha_G\) se minimiza minimizando\(\sigma_s/\sqrt{\epsilon_r}\). Curiosamente las dimensiones físicas\(a\) y no\(b\) tienen ningún efecto discernible sobre\(\alpha_G\). Ahora consideramos\(\alpha_R\):
\ begin {align}\ alpha_r &\ triangleq\ frac {R'} {2Z_0}\ nonumber\\ & =\ frac {1} {2}\ frac {\ izquierda (1/ 2\ pi\ delta_ {ic}\ sigma_ {ic}\ derecha)\ izquierda [1/a + C/b\ derecha]} {\ izquierda (1/2\ pi derecha\)\ izquierda (\ eta_0/\ sqrt {\ epsilon_r}\ derecha)\ ln\ izquierda (b/a\ derecha)}\ nonumber\\ &=\ frac {\ sqrt {\ epsilon_r}} {2\ eta_0\ delta_ {ic}\ sigma_ {ic}}\ cdot\ frac {\ izquierda [1/a + C/b\ derecha]} {\ ln\ izquierda (b/a\ derecha)}\ end {align}
Ahora haciendo la sustitución\(\delta_{ic} = \sqrt{2/\omega\mu_0\sigma_{ic}}\) para hacer explícitas las dependencias de los parámetros constitutivos, encontramos:
\[\alpha_R = \frac{1}{2\sqrt{2}\cdot\eta_0} \sqrt{\frac{\omega\mu_0 \epsilon_r}{\sigma_{ic}}} \cdot \frac{ \left[ 1/a + C/b \right] }{ \ln\left(b/a\right) } \nonumber \]
Aquí vemos que\(\alpha_R\) se minimiza minimizando\(\epsilon_r/\sigma_{ic}\). No es de extrañar ver que debemos maximizar\(\sigma_{ic}\). No obstante, es un poco sorprendente que debamos minimizar\(\epsilon_r\). Además, esto está en contraste con\(\alpha_G\), que se minimiza maximizando\(\epsilon_r\). Claramente hay que hacer una compensación aquí. Para determinar los parámetros de esta compensación, primero tenga en cuenta que el resultado depende de la frecuencia: Dado que\(\alpha_R\) domina\(\alpha_G\) a una frecuencia suficientemente alta (como se demuestra en la Figura\(\PageIndex{2}\)), parece que deberíamos minimizar\(\epsilon_r\) si la frecuencia de operación pretendida es suficientemente alta ; de lo contrario, el valor óptimo depende de la frecuencia. Sin embargo,\(\sigma_s\) puede variar en función de\(\epsilon_r\), por lo que una conclusión general sobre los valores óptimos de\(\sigma_s\) y no\(\epsilon_r\) es apropiada.
No obstante, también vemos que\(\alpha_R\) —a diferencia\(\alpha_G\) — depende de\(a\) y\(b\). Esto implica la existencia de una geometría generalmente óptima. Para encontrar esta geometría, minimizamos\(\alpha_R\) tomando la derivada con respecto a\(a\), estableciendo el resultado igual a cero, y resolviendo para\(a\) y/o\(b\). Aquí vamos:
\[\frac{\partial}{\partial a}\alpha_R = \frac{1}{2\sqrt{2}\cdot\eta_0} \sqrt{\frac{\omega\mu_0 \epsilon_r}{\sigma_{ic}}} \cdot \frac{\partial}{\partial a} \frac{\left[ 1/a + C/b \right] }{ \ln\left(b/a\right) } \label{m0189_eDAlpha} \]
Esta derivada se elabora en una adenda al final de esta sección. Usando el resultado de la adición, el lado derecho de la Ecuación\ ref {M0189_EDAlpha} se puede escribir de la siguiente manera:
\[\frac{1}{2\sqrt{2}\cdot\eta_0} \sqrt{\frac{\omega\mu_0 \epsilon_r}{\sigma_{ic}}} \cdot \left[ \frac{-1}{a^2 \ln\left(b/a\right) } + \frac{ 1/a + C/b }{a \ln^2\left(b/a\right) } \right] \label{m0189_eDAlpha2} \]
Para que\(\partial\alpha_R/\partial a=0\), el factor entre corchetes anteriores debe ser igual a cero. Después de unos pasos de álgebra, encontramos:
\[\ln\left(b/a\right) = 1+\frac{C}{b/a} \nonumber \]
En el Caso I (\(\sigma_{oc} \gg \sigma_{ic}\)),\(C=0\) entonces:
\[b/a=e\cong 2.72 ~~~ \mbox{(Case I)} \nonumber \]
En el Caso II (\(\sigma_{oc} = \sigma_{ic}\)),\(C=1\). La ecuación resultante se puede resolver trazando la función, o por algunas iteraciones de prueba y error; de cualquier manera uno encuentra rápidamente
\[b/a\cong 3.59 ~~~ \mbox{(Case II)} \nonumber \]
Resumiendo, hemos encontrado que\(\alpha\) se minimiza al elegir la relación de los radios externo e interno para que esté en algún lugar entre\(2.72\) y\(3.59\), con el valor preciso dependiendo de la conductividad relativa de los conductores interno y externo.
Sustituyendo estos valores de\(b/a\) en la Ecuación\ ref {M0189_EZ0cc}, obtenemos:
\[Z_0 \approx \frac{59.9~\Omega}{\sqrt{\epsilon_r}} ~~\mbox{to}~~ \frac{76.6~\Omega}{\sqrt{\epsilon_r}} \label{m0189_eZ0Opt} \]
como el rango de impedancias de cable coaxial correspondientes a diseños físicos que minimizan la atenuación.
La ecuación\ ref {M0189_EZ0opt} da el rango de impedancias características que minimizan la atenuación para líneas de transmisión coaxiales. El valor preciso dentro de este rango depende de la relación entre la conductividad del conductor externo y la del conductor interno.
Ya que\(\epsilon_r\ge 1\), la impedancia que minimiza la atenuación es menor para los cables llenos de dieléctricos que para los cables llenos de aire. Por ejemplo, volvamos a considerar el RG-59 de Ejemplo\(\PageIndex{1}\). En ese caso,\(\epsilon_r\cong 2.25\) y\(C=0\), indicar\(Z_0\approx 39.9~\Omega\) es óptimo para la atenuación. La impedancia característica real de\(Z_0\) es aproximadamente\(75~\Omega\), por lo que claramente RG-59 no está optimizado para la atenuación. Esto se debe simplemente a que se aplican otras consideraciones, incluida la capacidad de manejo de energía (abordada en la Sección 7.4) y la conveniencia de los valores estándar (abordados en la Sección 7.5).
Adenda: Derivada de\(a^2\ln(b/a)\)
Evaluación de la Ecuación\ ref {M0189_EDAlpha} requiere encontrar la derivada de\(a^2\ln(b/a)\) con respecto a\(a\). Usando la regla de la cadena, encontramos:
\ begin {align}\ frac {\ parcial} {\ parcial a}\ izquierda [a^2\ ln\ izquierda (\ frac {b} {a}\ derecha)\ derecha] = &\ izquierda [\ frac {\ parcial} {\ parcial a} a^2\ derecha]\ ln\ izquierda (\ frac {b} {a}\ derecha)\ nonumber\\ + &a^2\ izquierda [\ frac {\ parcial} {\ parcial a}\ ln\ izquierda (\ frac {b} {a}\ derecha)\ derecha]\ end {align}
Nota
\[\frac{\partial}{\partial a} a^2 = 2a \nonumber \]
y
\ begin {align}\ frac {\ parcial} {\ parcial a}\ ln\ izquierda (\ frac {b} {a}\ derecha) &=\ frac {\ parcial} {\ parcial} {\ parcial a}\ izquierda [\ ln\ izquierda (b\ derecha) -\ ln\ izquierda (a\ derecha)\ derecha]\ nonumber\\ &=-\ frac {\ parcial} {\ parcial a}\ ln\ izquierda (a\ derecha)\ nonumber\\ &=-\ frac {1} {a}\ end {align}
Entonces:
\ begin {align}\ frac {\ parcial} {\ parcial a}\ izquierda [a^2\ ln\ izquierda (\ frac {b} {a}\ derecha)\ derecha] &=\ izquierda [2a\ derecha]\ ln\ izquierda (\ frac {b} {a}\ derecha) + a^2\ izquierda [-\ frac {1} {a}\ derecha]\ nonumber\\ &=\ en caja {2a\ ln\ izquierda (\ frac {b} {a}\ derecha) - a}\ end {align}
Este resultado se sustituye\(a^2\ln(b/a)\) en la Ecuación\ ref {M0189_EDAlpha} para obtener la Ecuación\ ref {M0189_EDAlpha2}.


