3.3: La ecuación de Schrödinger no lineal
- Page ID
- 84962
Si ambos efectos, dispersión y modulación de autofase, actúan simultáneamente sobre el pulso, la envolvente de campo obedece a la ecuación
\[j\dfrac{\partial A(z,t)}{\partial z} = -D_2 \dfrac{\partial^2 A}{\partial t^2} + \delta |A|^2 A,\label{eq3.3.1} \]
Esta ecuación se llama Ecuación de Schrödinger no lineal (NSE) -si ponemos la unidad imaginaria en el lado izquierdo- ya que tiene la forma de una Ecuación de Schrödinger. Se llama no lineal, porque la energía potencial se deriva del cuadrado de la función de onda misma. Como hemos visto en la discusión en las últimas secciones, la dispersión positiva y la modulación de autofase positiva conducen a una redistribución similar de los componentes espectrales. Esto mejora la propagación del pulso en el tiempo. Sin embargo, si tenemos dispersión negativa, es decir, un paquete de ondas con alta frecuencia portadora viaja más rápido que un paquete de onda con una frecuencia portadora baja, entonces, los paquetes de onda de alta frecuencia generados por la modulación de autofase en la parte delantera del pulso tienen la oportunidad de ponerse al día con el pulso en sí debido a la dispersión negativa. Lo contrario es el caso de las bajas frecuencias. Esta disposición da como resultado pulsos que ya no se dispersan, es decir, ondas solitarias. Esa dispersión negativa es necesaria para compensar el efecto positivo de Kerr también es evidente a partir del NSE (\(\ref{eq3.3.1}\)). Porque, para un efecto Kerr positivo, la energía potencial en el NSE siempre es negativa. Solo hay soluciones ligadas, es decir, ondas solitarias brillantes, si el término de energía cinética, es decir, la dispersión, tiene un signo negativo,\(D_2 < 0\).
Solitones del NSE
A continuación, estudiamos diferentes soluciones del NSE para el caso de dispersión negativa y modulación positiva de autofase. No pretendemos dar una visión general completa sobre la solución muchas veces del NSE en toda su profundidad matemática aquí, porque no es necesario para lo siguiente. Esto se puede encontrar en detalle en otra parte [4, 5, 6, 7].
Sin pérdida de generalidad, por normalización de la amplitud de campo
\[A = \dfrac{A'}{\tau} \sqrt{\dfrac{2D_2}{\delta}}, \nonumber \]
la distancia de propagación\(z = z' \cdot \tau^2/D_2\), y el tiempo\(t = t'\cdot \tau\), el NSE (3.3) con dispersión negativa siempre se puede transformar en la forma normalizada
\[j \dfrac{\partial A'(z',t)}{\partial z'} = \dfrac{\partial^2 A'}{\partial t'^2} + 2 |A|^2 A'\label{eq3.3.2} \]
Esto equivale a establecer\(D_2 = -1\) y\(\delta = 2\). Para las simulaciones numéricas, que se muestran en los capítulos siguientes, simulamos la Ecuación normalizada (\(\ref{eq3.3.2}\)) y los ejes están en unidades normalizadas de posición y tiempo.
Soliton Fundamental
Buscamos una función de onda estacionaria del NSE (\(\ref{eq3.3.1}\)), tal que su cuadrado absoluto sea un potencial autoconsistente. Un potencial de ese tipo es bien conocido por la Mecánica Cuántica, el\(sech^2\) -Potencial [8], y por lo tanto la forma del pulso solitario es un sech
\[A_s(z,t) = A_0 \text{sech }(\dfrac{t}{\tau}) e^{-j\theta}, \nonumber \]
donde\(\theta\) está el desplazamiento de fase no lineal del solitón
\[\theta = \dfrac{1}{2} \delta A_0^2 z\label{eq3.3.4} \]
El desplazamiento de fase de la solción es constante sobre el pulso con respecto al tiempo en contraste con el caso de la modulación de autofase solamente, donde el desplazamiento de fase es proporcional a la potencia instantánea. El equilibrio entre los efectos no lineales y los efectos lineales requiere que el desplazamiento de fase no lineal sea igual a la dispersión dispersiva del pulso
\[\theta = \dfrac{|D_2|}{\tau^2}z. \nonumber \]
Dado que la amplitud de campo\(A(z, t)\) está normalizada, de tal manera que el cuadrado absoluto es la intensidad, la fluencia de energía solitónica viene dada por
\[w = \int_{-\infty}^{\infty} |A_s (z, t)|^2 dt = 2A_0^2 \tau.\label{eq3.3.6} \]
De eqs. (\(\ref{3.3.4}\)) a (\(\ref{3.3.6}\)), obtenemos para fluencia de energía de pulso constante, que el ancho del solitón es proporcional a la cantidad de dispersión negativa
\[\tau = \dfrac{4|D_2|}{\delta w}. \nonumber \]
Tenga en cuenta que el área de pulso para un solitón fundamental solo está determinada por la dispersión y el coeficiente de modulación de autofase
\[\text{Pulse Area } = \int_{-\infty}^{\infty} |A_s (z, t)|dt = \pi A_0 \tau = \pi \sqrt{\dfrac{|D_2|}{2\delta}}. \nonumber \]
Así, un pulso inicial con un área diferente no puede simplemente convertirse en un solitón puro.
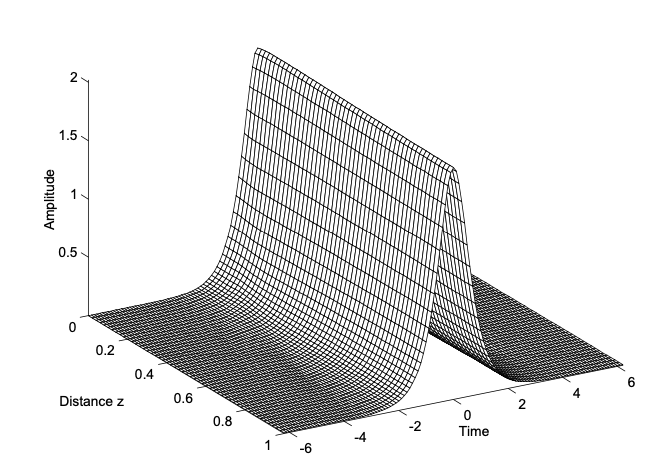
La Figura 3.3 muestra la solución numérica del NSE para el pulso de solitón fundamental. La distancia, tras la cual el solitón adquiere un desplazamiento de fase de\(\pi/4\), se denomina periodo solitón, por razones, que quedarán claras en la siguiente sección.
Dado que la dispersión es constante sobre la frecuencia, es decir, el NSE no tiene dispersión de orden superior, la frecuencia central del solitón se puede elegir arbitrariamente. Sin embargo, debido a la dispersión, las velocidades de grupo de los solitones con diferentes frecuencias portadoras serán diferentes. Uno encuentra fácilmente por una transformación de Gallilei en un marco móvil, que el NSE posee la siguiente solución de soliton fundamental general
\[A_s (z,t) = A_0 \text{sech} (x(z,t)) e^{-j \theta (z, t)}, \nonumber \]
con
\[x = \dfrac{1}{\tau} (t - 2|D_2|p_0 z - t_0), \nonumber \]
y un desplazamiento de fase no lineal
\[\theta = p_0 (t - t_0) + |D_2| \left (\dfrac{1}{\tau^2} - p_0^2 \right ) z + \theta_0. \nonumber \]
Así, la fluencia\(w\) o amplitud de energía\(A_0\), la frecuencia portadora\(p_0\), la fase\(\theta_0\) y el origen\(t_0\), es decir, la temporización del solitón fundamental aún no están determinadas. Solo se fija el área de soliton. La fluencia energética y la anchura se determinan si se especifica una de ellas, dada una cierta dispersión y coeficiente SPM.
Solitones de orden superior
El NSE tiene dispersión constante, en nuestro caso dispersión negativa. Eso significa que la velocidad del grupo depende linealmente de la frecuencia. Suponemos, que dos solciones fundamentales están muy alejadas entre sí, para que no interactúen. Entonces esta superpositon lineal es para todos los fines prácticos otra solución del NSE. Si elegimos la frecuencia portadora del solitón, comenzando en un momento posterior, superior a la del solitón de enfrente, el solitón posterior alcanzará al solitón principal debido a la dispersión negativa y los pulsos chocarán.
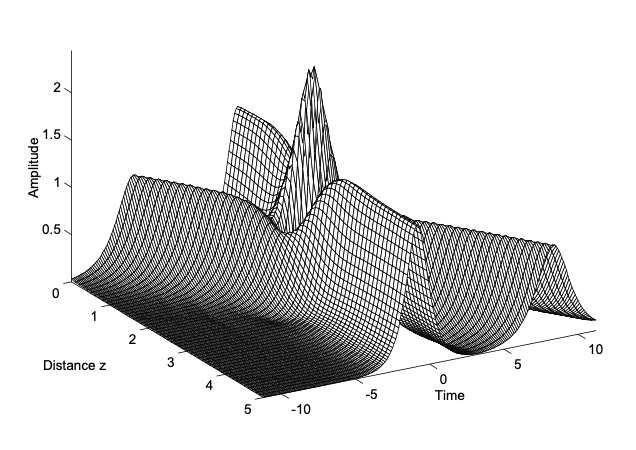
La figura 3.4 muestra esta situación. Obviamente, los dos pulsos se recuperan completamente de la colisión, es decir, el NSE tiene verdaderas soluciones de solitón. Los solitones tienen propiedades similares a partículas. Una solución, compuesta por varios solitones fundamentales, se llama solitón de orden superior. Si miramos más de cerca a la figura 3.4, reconocemos, que el solitón en reposo en el marco de tiempo local, y que sigue la\(t = 0\) línea sin la colisión, es algo empujado hacia adelante debido a la colisión. Un análisis detallado de la colisión también mostraría, que las fases de los solitones han cambiado [4]. Los cambios de fase debidos a las colisiones de solitones se utilizan para construir todos los interruptores ópticos [10], utilizando interferómetros Mach-Zehnder plegados, los cuales pueden ser realizados de manera autoestabilizada por bucles de fibra Sagnac.
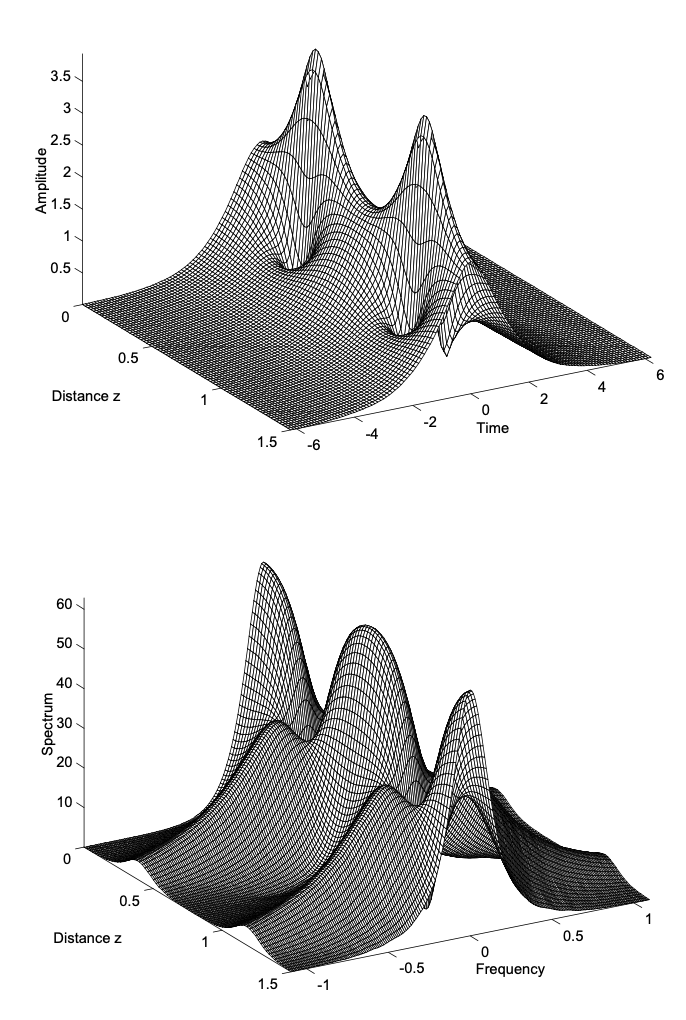
El NSE también muestra soluciones solitónicas de orden superior, que viajan a la misma velocidad, es decir, poseen la misma frecuencia portadora, las llamadas soluciones de respiradero. Las figuras 3.5 (a) y (b) muestran la amplitud y el espectro de dicha solución de solitón de orden superior, que tiene el doble de área del solitón fundamental. La simulación comienza con un pulso sech-pulso, que tiene el doble de área del solitón fundamental, mostrado en la figura 3.3. Debido a la interacción de los dos solitones, la forma temporal y el espectro presentan un comportamiento complicado pero periódico. Este periodo es el periodo solitón\(z = \pi/4\), como se mencionó anteriormente. Como se puede observar en las Figuras 3.5 (a) y 3.5 (b), la dinámica de solitones de orden superior conduce a un enorme acortamiento del pulso después de la mitad del período solitón. Este proceso ha sido utilizado por Mollenauer, para construir su láser solitón [11]. En el láser de solitón, la compresión de pulsos, que ocurre para un solitón de orden superior como se muestra en la Figura 3.5 (a), se explota para el modelocking. Mollenauer fue pionera en la propagación de solitones en fibras ópticas, como propusieron Hasegawa y Tappert [3], con el láser de solitón, que produjo los primeros pulsos de picosegundos a 1.55\(\mu\) m. Haus [12] da un relato detallado del láser solitón.
Hasta el momento, hemos discutido las soluciones de solitón puro del NSE. Pero, ¿qué sucede si se inicia la propagación con un pulso de entrada que no corresponde a un solitón fundamental o de orden superior?
Teoría de Dispersión Inversa
Obviamente, el NSE cuenta con soluciones, las cuales están compuestas por solitones fundamentales. Así, las soluciones obedecen a cierto principio de superposición que resulta absolutamente sorprendente para un sistema no lineal. Por supuesto, no son posibles superposiciones arbitrarias como en un sistema lineal. La razón más profunda de la solución múltiples del NSE se puede encontrar mediante el estudio de sus propiedades físicas y matemáticas. La base matemática para una formulación analítica de las soluciones al NSE es la teoría de dispersión inversa [13, 14, 4, 15]. Es un método tranforme espectral para resolver ecuaciones de onda no lineales integrables, similar a la transformada de Fourier para la solución de ecuaciones de onda lineal [16].
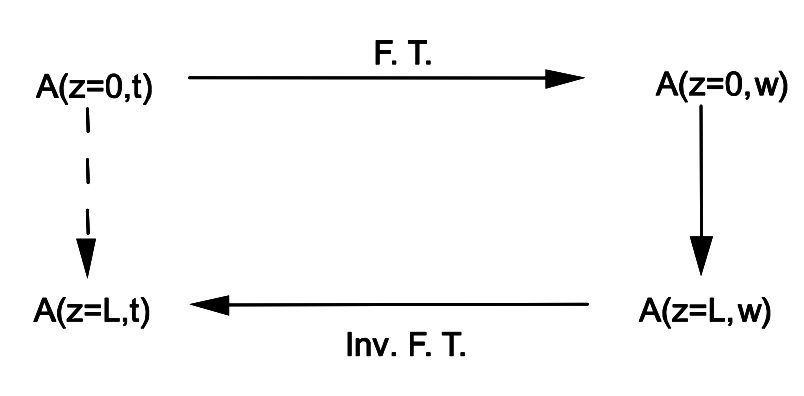
Recordemos brevemente, cómo resolver un problema de valor inicial para una ecuación diferencial parcial lineal (p.d.e.), como la Ecuación (2.6.12), que trata el caso de una propagación de pulsos puramente dispersiva. El método se esboza en la Figura 3.6. Fourier tranformamos el pulso inicial en el dominio espectral, porque, las funciones exponenciales son soluciones propias de los operadores diferenciales con coeficientes constantes. El lado derecho de (2.6.12) solo está compuesto por potencias del operador diferencial, por lo tanto los exponenciales son funciones propias del lado derecho completo. Así, después de la transformación de Fourier, el p.d.e. se convierte en un conjunto de ecuaciones diferenciales ordinarias (o.d.e.), una para cada onda parcial. La excitación de cada onda viene dada por el espectro de la onda inicial. Los valores propios del operador diferencial, que constituye el lado derecho de (2.6.12), viene dado por la relación de dispersión,\(k(\omega)\), hasta la unidad imaginaria. La solución del o.d.e restante es entonces un exponencial simple de la relación de dispersión. Ahora, tenemos el espectro de la onda propagada y por transformación inversa de Fourier, es decir, sumamos sobre todas las ondas parciales, encontramos la nueva forma temporal del pulso propagado.
Como en el caso del método de transformada de Fourier para la solución de ecuaciones de onda lineal, la teoría de dispersión inversa se basa nuevamente en una transformada espectral, (Fig.3.7). Sin embargo, esta transformación depende ahora de los detalles de la ecuación de onda y de las condiciones iniciales. Esta dependencia conduce a un principio de superposición modificado. Como se muestra en [7], se puede formular para muchas ecuaciones de ondas no lineales integrables un problema de dispersión relacionado como lo hace en la Teoría Cuántica para la dispersión de una partícula en un pozo potencial. Sin embargo, el pozo potencial ahora está determinado por la solución de la ecuación de onda. Así, el potencial inicial ya viene dado por las condiciones iniciales. Los estados estacionarios del problema de dispersión, que son las soluciones propias del hamiltoniano correspondiente, son los analógicos a las oscilaciones complejas monocromáticas, que son las funciones propias del operador diferencial. Los valores propios son el análogo a la relación de dispersión, y como en el caso de las p.d.e lineales, las soluciones propias obedecen a o.d.e lineales simples.
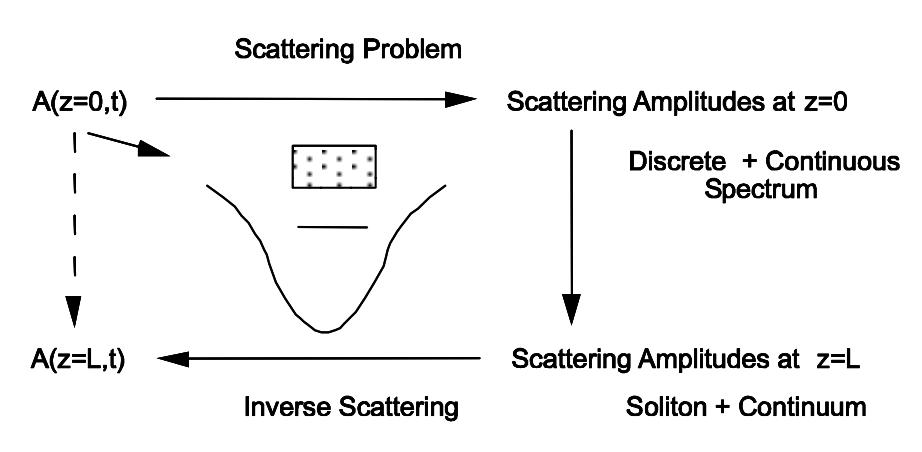
Un potencial dado tendrá un cierto número de estados unidos, que corresponden al espectro discreto y un continuo de estados de dispersión. La característica del espectro continuo de valores propios es el coeficiente de reflexión para las ondas dispersas tras la reflexión en el potencial. Así, un cierto potencial, es decir, una determinada condición inicial, tiene un cierto espectro discreto y continuo con un coeficiente de reflexión correspondiente. A partir de la teoría de dispersión inversa para problemas de dispersión cuántica mecánica y electromagnética, sabemos, que el potencial puede ser reconstruido a partir de los datos de dispersión, es decir, el coeficiente de reflexión y los datos para el espectro discreto [?]. Esto es cierto para una clase muy general de potenciales de dispersión. Como casi se puede adivinar ahora, los estados propios discretos de las condiciones iniciales conducirán a soluciones solitónicas. Ya hemos estudiado la dinámica de algunas de estas soluciones solitónicas anteriormente. El espectro continuo conducirá a una onda dispersiva que se llama continuo. Así, la solución más general del NSE, para determinadas condiciones iniciales arbitrarias, es una superposición de un solitón, tal vez un solitón de orden superior, y una contribución continua.
El continuum se dispersará durante la propagación, de manera que solo se reconoce el solitón después de un tiempo. Así, el continuum se convierte en una contribución asintóticamente pequeña a la solución del NSE. Por lo tanto, la dinámica del continuo se describe completamente por la relación de dispersión lineal de la ecuación de onda.
La transformación posterior del dominio espectral al tiempo no es tan simple como en el caso de la transformada de Fourier para p.d.e lineales. Se tiene que resolver una ecuación integral lineal, la ecuación de Marchenko [17]. Sin embargo, la solución de una ecuación no lineal se ha reducido a la solución de dos problemas lineales, lo que es un tremendo éxito.
Para apreciar estas propiedades de las soluciones del NSE, resolvemos el NSE para un pulso inicial de forma rectangular. El resultado se muestra en la Figura 3.8.
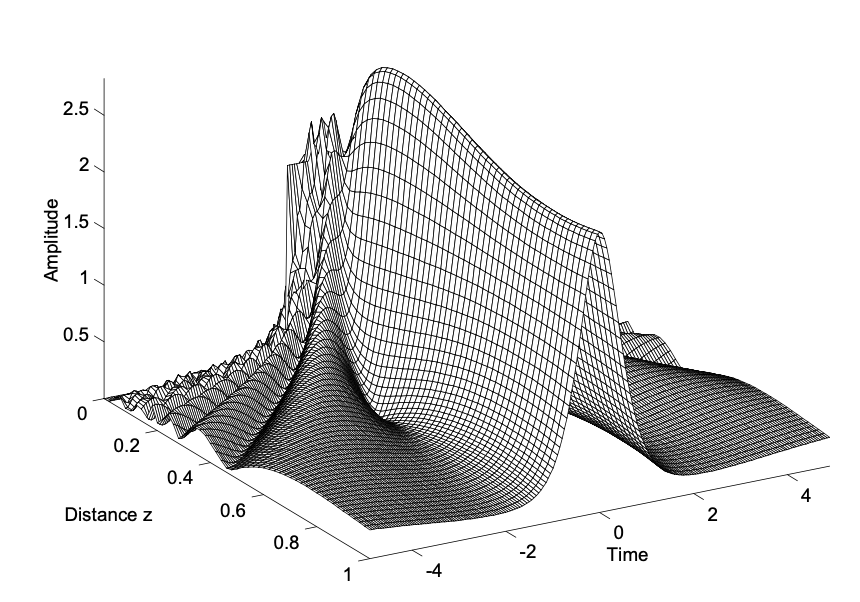
El problema de dispersión, que tiene que resolverse para esta condición inicial, es el mismo que para una partícula no relativista en una caja rectangular de potencial [32]. La profundidad del potencial se elige lo suficientemente pequeña, para que tenga un solo estado ligado. Así, partimos de una onda compuesta por un solitón fundamental y un continuum. Es fácil reconocer la contribución del continuo, es decir, la onda dispersiva, que se separa del solitón durante la propagación. Esta solución ilustra, que la conformación del pulso de solitón debido a la presencia de dispersión y modulación de autofase puede tener un fuerte impacto en la generación de pulsos [18]. Cuando la dispersión y la modulación de autofase se ajustan correctamente, la formación de solitones puede conducir a pulsos muy limpios, estables y extremadamente cortos en un láser de modo bloqueado.


