3.5: Teoría de la Perturbación del Solitón

De la discusión anterior, tenemos pleno conocimiento sobre las posibles soluciones del NSE que describe un sistema hamiltoniano especial. Sin embargo, el NSE apenas describe un sistema físico real como, por ejemplo, una fibra óptica real en todos sus aspectos [21, 22]. De hecho, el propio NSE, como hemos visto durante la derivación en las secciones anteriores, es solo una aproximación a la ecuación de onda completa. Se aproximó la relación de dispersión por una parábola a la frecuencia portadora supuesta del solitón. También el efecto Kerr instantáneo descrito por un índice de refracción dependiente de la intensidad es solo una aproximación a la\(\chi^{(3)}\) no linealidad real de un medio Kerr-medio [23, 24]. Por lo tanto, lo más importante es estudiar qué sucede con una solución solitónica del NSE debido a efectos perturbadores como dispersión de orden superior, tiempos de respuesta finitos de los no linearios, ganancia y ancho de banda de ganancia finita de amplificadores, que compensan la inevitable pérdida en un sistema real.

La investigación de solitones bajo perturbaciones es tan antigua como los solitones mismos. Muchos autores tratan los efectos perturbadores en el dominio de dispersión [25, 26]. Sólo recientemente se ha desarrollado una teoría de perturbación basada en el NSE linealizado, que es mucho más ilustrativa que una formulación en las amplitudes de dispersión. Este fue utilizado por primera vez por Haus [27] y formulado rigurosamente por Kaup [28]. En esta sección, presentaremos este enfoque en la medida en que sea indispensable para lo siguiente.

Un sistema, donde los procesos físicos más importantes son la dispersión y la modulación de autofase, es descrito por el NSE complementado con algún término de perturbación\(F\)

\[\dfrac{\partial A (z, t)}{\partial z} = -j \left [|D_2| \dfrac{\partial^2 A}{\partial t^2} + \delta |A|^2 A \right ] + F(A, A^*, z).\label{eq3.5.1} \]

A continuación, nos interesa lo que sucede con una solución de la ecuación completa (\(\ref{eq3.5.1}\)) que está muy cerca de un solitón fundamental, i.e.

\[A(z, t) = \left [a\left(\dfrac{t}{\tau}\right) + \Delta A(z, t) \right ] e^{-jk_s z}.\label{eq3.5.2} \]

Aquí,\(a(x)\) está el solitón fundamental según la eq. (3.3.3)

\[a(\dfrac{t}{\tau}) = A_0 \text{sech} (\dfrac{t}{\tau}), \nonumber \]

y

\[k_s = \dfrac{1}{2} \delta A_0^2 \nonumber \]

es el desplazamiento de fase del solitón por unidad de longitud, es decir, el vector de onda de solción.

Una desviación del solitón ideal puede surgir ya sea por el término de conducción adicional\(F\) en el lado derecho o por una desviación ya presente en la condición inicial. Usamos la forma (\(\ref{eq3.5.2}\)) como ansatz para resolver el NSE a primer orden en la perturbación\(\Delta A\), es decir, linealizamos el NSE alrededor del solitón fundamental y obtenemos para la perturbación

\[\dfrac{\partial \Delta A}{\partial z} = -j k_s \left [\left(\dfrac{\partial^2}{\partial x^2} - 1\right) \Delta A + 2 \text{sech}^2(x) (2 \Delta A + \Delta A^*) \right ] + F(A, A^*, z) e^{jk_s z}, \label{eq3.5.5} \]

donde\(x = t/\tau\). Debido a la no linealidad, el campo se acopla a su complejo conjugado. Por lo tanto, la eq. (\(\ref{eq3.5.5}\)) corresponde en realidad a dos ecuaciones, una para la amplitud y otra para su complejo conjugado. Por lo tanto, introducimos la notación vectorial

\[\Delta A = \left (\begin{matrix} \Delta A \\ \Delta A^* \end{matrix} \right ). \nonumber \]

Introducimos además la distancia de propagación normalizada\(z' = k_s z\) y el tiempo normalizado\(x = t/\tau\). El NSE perturbado linealizado es dado entonces por

\[\dfrac{\partial}{\partial z'} \Delta A = L \Delta A + \dfrac{1}{k_s} F(A, A^*, z) e^{jz'}\label{eq3.5.7} \]

Aquí,\(\text{L}\) es el operador que surge de la linealización del NSE

\[\text{L} = -j \sigma_3 \left [(\dfrac{\partial^2}{\partial x^2} - 1) + 2 \text{sech}^2 (x) (2 + \sigma_1) \right ],\label{eq3.5.8} \]

donde\(\sigma_i, i = 1, 2, 3\) están las matrices Pauli. Para una solución de la ecuación no homogénea (\(\ref{eq3.5.7}\)), necesitamos las funciones propias y el espectro del operador diferencial\(\text{L}\). Encontramos en la sección 3.3.2, que el solitón fundamental tiene cuatro grados de libertad, cuatro parámetros libres. Esto da ya cuatro soluciones propias y soluciones principales conocidas del NSE linealizado, respectivamente. Están determinados por las derivadas de las soluciones generales fundamentales de solitón de acuerdo con las Ecuaciones (3.3.9) a (3.3.11) con respecto a los parámetros libres. Estas funciones propias son

\[\text{f}_w (x) = \dfrac{1}{w} (1 - x \tanh x) a(x) \left (\begin{matrix} 1 \\ 1 \end{matrix} \right ), \nonumber \]

\[\text{f}_{\theta} (x) = -j a(x) \left (\begin{matrix} 1 \\ -1 \end{matrix} \right ), \nonumber \]

\[\text{f}_p (x) = -j x \tau a(x) \left (\begin{matrix} 1 \\ -1 \end{matrix} \right ), \nonumber \]

\[\text{f}_t (x) = \dfrac{1}{\tau} \tanh (x) a(x) \left (\begin{matrix} 1 \\ 1 \end{matrix} \right ), \nonumber \]

y describen perturbaciones de la energía solitónica, fase, frecuencia portadora y temporización. Un componente de cada una de estas funciones vectoriales se muestra en la Figura 3.9.

Figura 3.9: Perturaciones en la amplitud del solitón (a), fase (b), frecuencia (c) y temporización (d). Figura por MIT OCW.

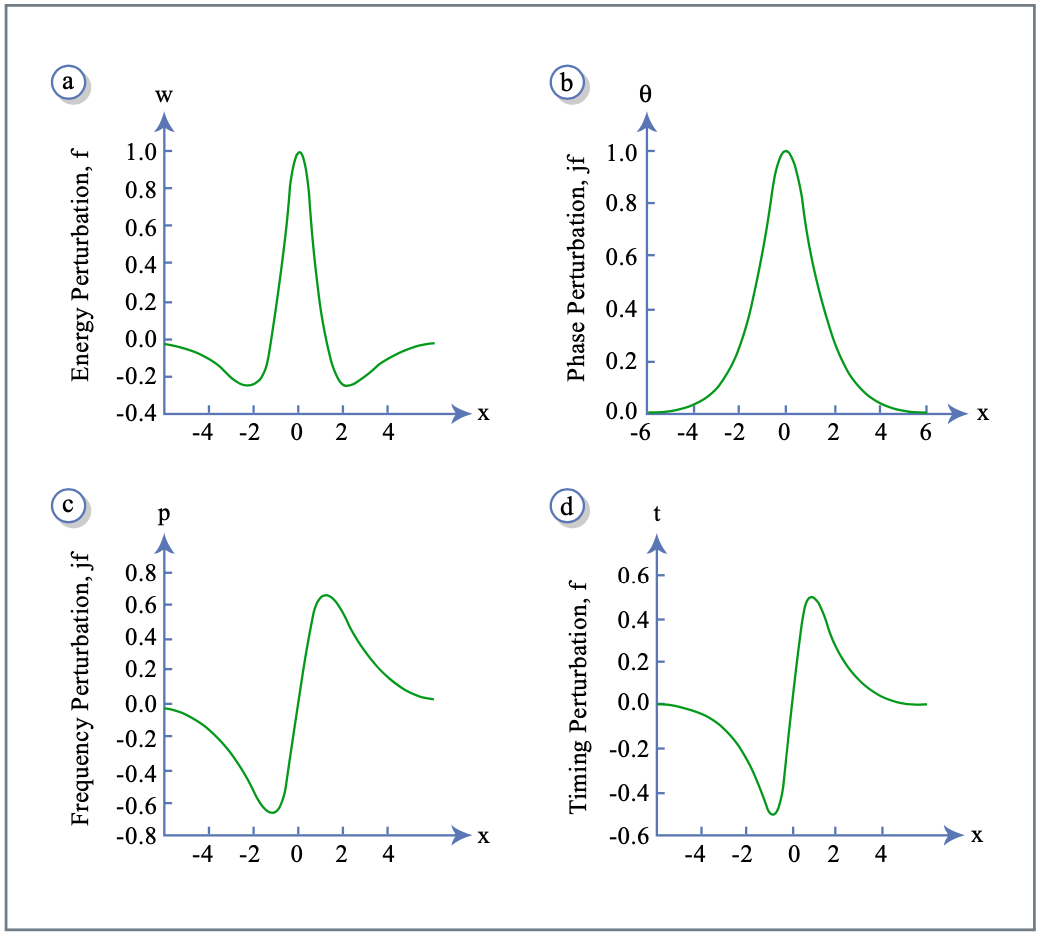
La acción del operador de evolución del NSE linealizado sobre estas perturbaciones solitónicas es

\[\text{Lf}_w = \dfrac{1}{w} \text{f}_{\theta},\label{eq3.5.13} \]

\[\text{Lf}_{\theta} = 0, \nonumber \]

\[\text{Lf}_p = -2\tau^2 f_t,\label{eq3.5.15} \]

\[\text{Lf}_t = 0.\label{eq3.5.16} \]

Las ecuaciones (\(\ref{eq3.5.13}\)) y (\(\ref{eq3.5.15}\)) indican, que las perturbaciones en la energía y la frecuencia portadora se convierten en fluctuaciones adicionales de fase y temporización del pulso debido a SPM y GVD. Esta es la base para exprimir solitones en fibras ópticas [27]. Las perturbaciones de sincronización y fase pueden aumentar sin límites, debido a que el sistema es autónomo, el origen para el efecto Gordon-Haus, [29] y no hay referencia de fase en el sistema. El espectro continuo completo del NSE linealizado ha sido estudiado por Kaup [28] y está dado por

\[\text{Lf}_k = \lambda_k \text{f}_k, \nonumber \]

\[\lambda_k = j (k^2+1), \nonumber \]

\[\text{f}_k(x) = e^{-jkx} \left (\begin{matrix} (k-j \tanh x)^2 \\ \text{sech}^2 x \end{matrix} \right ),\label{eq3.5.19} \]

y

\[\text{L}\bar{\text{f}}_k = \bar{\lambda}_k \bar{f}_k, \nonumber \]

\[\bar{\lambda}_k = -j (k^2 + 1), \nonumber \]

\[\bar{f}_k = \sigma_1 f_k.\label{eq3.5.22} \]

Nuestra definición de las funciones propias es ligeramente diferente de Kaup [28], porque también definimos el producto interno en el espacio complejo como

\[< u|v > = \dfrac{1}{2} \int_{-\infty}^{+\infty} u^+ (x) v(x) dx.\label{eq3.5.23} \]

Adoptando esta definición, el producto interno de un vector consigo mismo en el subespacio donde el segundo componente es el conjugado complejo del primer componente es la energía de la señal, una cantidad física.

El operador no\(L\) se une a sí mismo con respecto a este producto interno. El origen físico de esta propiedad matemática es, que el sistema linealizado no conserva energía debido al bombeo paramétrico por el solitón. Sin embargo, desde (\(\ref{eq3.5.8}\)) y (\(\ref{eq3.5.23}\)), podemos ver fácilmente que el operador adjunto viene dado por

\[\text{L}^{+} = -\sigma_3 \text{L} \sigma_3, \nonumber \]

y por lo tanto, obtenemos para el espectro del operador adjunto

\[\text{L}^{+} \text{f}_k^{(+)} = \lambda_{k}^{(+)} \text{f}_k^{(+)},\label{eq3.5.25} \]

\[\lambda_{k}^{(+)} = -j (k^2 + 1), \nonumber \]

\[\text{f}_k^{(+)} = \dfrac{1}{\pi (k^2 + 1)^2} \sigma_3 \text{f}_k, \nonumber \]

y

\[\text{L}^{+} \bar{\text{f}}_k^{(+)} = \bar{\lambda}_{k}^{(+)} \bar{\text{f}}_k^{(+)}, \nonumber \]

\[\bar{\lambda}_{k}^{(+)} = j (k^2 + 1), \nonumber \]

\[\bar{\text{f}}_k^{(+)} = \dfrac{1}{\pi (k^2 + 1)^2} \sigma_3 \bar{\text{f}}_k, \nonumber \]

Las funciones propias a\(\text{L}\) y su unión son mutuamente ortogonales entre sí, y ya están normalizadas adecuadamente

\[<\text{f}_k^{(+)}|\text{f}_{k'} > = \delta (k - k')\nonumber \]

\[<\bar{\text{f}}_k^{(+)}|\bar{\text{f}}_{k'} > = \delta (k - k')\nonumber \]

\[<\bar{\text{f}}_k^{(+)}|\text{f}_{k'} > = <\text{f}_k^{(+)} |\bar{\text{k}}_{k'} >=0.\nonumber \]

Este sistema, que describe las excitaciones continuas, se completa tomando también en cuenta las perturbaciones de los cuatro grados de libertad del solitón (\(\ref{eq3.5.13}\)) - (\(\ref{eq3.5.16}\)) y sus anexos

\[\text{f}_w^{(+)} (x) = j 2 \tau \sigma_3 \text{f}_{\theta} (x) = 2 \tau a(x) \left ( \begin{matrix} 1 \\ 1 \end{matrix} \right ),\label{eq3.5.31} \]

\[\begin{array} {rcl} {\text{f}_{\theta}^{(+)} (x)} & = & {-2j \tau \sigma_3 \text{f}_w (x)} \\ {} & = & {\dfrac{-2j\tau}{w} (1 - x \tanh x) a(x) \left ( \begin{matrix} 1 \\ -1 \end{matrix} \right ),}\end{array} \nonumber \]

\[\text{f}_p^{(+)} (x) = -\dfrac{2j\tau}{w} \sigma_3 \text{f}_t (x) = \dfrac{2i}{w} \tanh a(x) \left ( \begin{matrix} 1 \\ -1 \end{matrix} \right ), \nonumber \]

\[\text{f}_t^{(+)} (x) = \dfrac{2j\tau}{w} \sigma_3 \text{f}_p (x) = \dfrac{2 \tau^2}{w} xa(x) \left ( \begin{matrix} 1 \\ 1 \end{matrix} \right ). \nonumber \]

Ahora, la unidad se puede descomponer en dos proyecciones, una sobre el continuo y otra sobre la perturbación de las variables de solitón [28]

\[\begin{array} {rcl} {\delta (x - x')} & = & {\int_{-\infty}^{\infty} dk [|\text{f}_k >< \text{f}_k^{(+)}| + |\bar{\text{f}}_{k} >< \bar{\text{f}}_{k}^{(+)}|]} \\ {} & + & {|\text{f}_w >< \text{f}_w^{(+)}| + |\text{f}_{\theta} >< \text{f}_{\theta}^{(+)}|} \\ {} & + & {|\text{f}_p >< \text{f}_p^{(+)}| + |\text{f}_t >< \text{f}_t^{(+)}|}. \end{array} \nonumber \]

Cualquier desviación se\(\Delta A\) puede descomponer en una contribución que conduzca a un solitón con un desplazamiento en los cuatro parámetros de solitón y una contribución continua\(a_c\)

\[\Delta A (z') = \Delta w (z') \text{f}_w + \Delta \theta (z') \text{f}_{\theta} + \Delta p(z') \text{f}_p + \Delta t(z') \text{f}_t + \text{a}_c (z').\label{eq3.5.36} \]

Además, el continuum puede escribirse como

\[\text{a}_c = \int_{-\infty}^{\infty} dk [g(k) \text{f}_k (x) + \bar{g} (k) \bar{\text{f}}_k (x)].\label{eq3.5.37} \]

Si ponemos la descomposición (\(\ref{eq3.5.36}\)) en (\(\ref{eq3.5.7}\)) obtenemos

\[\dfrac{\partial \Delta w}{\partial z'} \text{f}_w + \dfrac{\partial \Delta \theta}{\partial z'} \text{f}_{\theta} + \dfrac{\partial \Delta p}{\partial z'} \text{f}_p + \dfrac{\partial \Delta t}{\partial z'} \text{f}_t + \dfrac{\partial}{\partial z'} \text{a}_c = \nonumber \]

\[\text{L} (\Delta w(z') \text{f}_w + \Delta p (z') \text{f}_p + \text{a} (z')_c) + \dfrac{1}{k_s} \text{F} (A, A^*, z') e^{-iz'}. \nonumber \]

Al construir los productos escalares (\(\ref{eq3.5.23}\)) de esta ecuación con las soluciones propias del operador de evolución adjunto (\(\ref{eq3.5.25}\)) to (\(\ref{eq3.5.31}\)) y usando los valores propios (\(\ref{eq3.5.13}\)) a (\(\ref{eq3.5.22}\)), encontramos

\[\dfrac{\partial}{\partial z'} \Delta w = \dfrac{1}{k_s} < \text{f}_w^{(+)} | \text{F} e^{jz'} >, \nonumber \]

\[\dfrac{\partial}{\partial z'} \Delta \theta = \dfrac{\Delta W}{W} + \dfrac{1}{k_s} < \text{f}_{\theta}^{(+)} | \text{F} e^{jz'} >, \nonumber \]

\[\dfrac{\partial}{\partial z'} \Delta p = \dfrac{1}{k_s} < \text{f}_p^{(+)} | \text{F} e^{jz'} >, \nonumber \]

\[\dfrac{\partial}{\partial z'} \Delta t = 2 \tau \Delta p + \dfrac{1}{k_s} < \text{f}_t^{(+)} | \text{F} e^{jz'} >, \nonumber \]

\[\dfrac{\partial}{\partial z'} g(k) = j(1 + k^2) g(k) + \dfrac{1}{k_s} < \text{f}_k^{(+)} \text{F}(A, A^*, z') e^{jz'} >.\label{3.5.43} \]

Tenga en cuenta que el continuum\(\text{a}_c\) tiene que estar en el subespacio definido por

\[\sigma_1 \text{a}_c = \text{a}_c^*.\label{eq3.5.44} \]

Los espectros del continuum\(g(k)\) y\(\bar{g}(k)\) están relacionados por

\[\bar{g} (k) = g(-k)^*. \nonumber \]

Luego, podemos calcular directamente el continuo a partir de su espectro usando (\(\ref{eq3.5.19}\)), (\(\ref{eq3.5.37}\)) y (\(\ref{eq3.5.44}\))

\[a_c = -\dfrac{\partial^2 G(x)}{\partial x^2} + 2 \tanh (x) \dfrac{\partial G(x)}{\partial x} - \tanh^2 (x) G(x) + G^* (x) \text{sech}^2 (x),\label{eq3.5.46} \]

donde\(G(x)\) es, hasta el factor de fase\(e^{iz'}\), la función asociada de Gordon [33]. Es la transformada inversa de Fourier del espectro

\[G(x) = \int_{-\infty}^{\infty} g(k) e^{ikx} dk.\label{eq3.5.47} \]

Ya que\(g(k)\) obedece eq. (\(\ref{eq3.5.44}\)), la función asociada de Gordon obedece a una ecuación dispersiva pura en ausencia de un término de conducción\(F\)

\[\dfrac{\partial G(z', x)}{\partial z'} = -j \left ( 1 + \dfrac{\partial ^2}{\partial x^2} \right ) G(z', x). \nonumber \]

Es instructivo observar el espectro del continuo cuando solo\(k_0\) está presente un modo continuo con frecuencia normalizada, i.e\(g(k) = \delta (k - k_0)\). Entonces según las Ecuaciones (\(\ref{eq3.5.46}\)) y (\(\ref{eq3.5.47}\)) tenemos

\[a_{c,k} (x) = [k_0^2 - 2j k_0 \tanh (x) - 1] e^{-jk_0x} + 2 \text{sech}^2 (x) \cos (x). \nonumber \]

El espectro de esta contribución continua es

\[\begin{array} {rcl} {\bar{a}_{c, k} (\omega)} & = & {2\pi (k_)^2 - 1) \delta (\omega - k_0) +2k_0 P.V. \left (\dfrac{2}{\omega - k_0} + \dfrac{\pi}{\sinh(\tfrac{\pi}{2} (\omega - k_0))} \right )} \\ {} & = & {+\pi \dfrac{\omega - k_0}{\sinh (\tfrac{\pi}{2} (\omega - k_0))} + \pi \dfrac{\omega + k_0}{\sinh (\tfrac{\pi}{2} (\omega + k_0))}}\end{array} \nonumber \]