3.6: Inestabilidades del Solitón por Perturbaciones Periódicas

Las perturbaciones periódicas de los solitones son importantes para comprender los láseres de pulso ultracortos, así como los sistemas de comunicación óptica de larga distancia [30, 31]. A lo largo de un sistema de transmisión de larga distancia, los pulsos tienen que ser amplificados periódicamente. En un sistema láser de modo bloqueado, la mayoría de las veces la no linealidad, dispersión y ganancia ocurren de manera agrupada. Los solitones que se propagan en estos sistemas son solamente solitones promedio, los cuales se propagan a través de componentes discretos de manera periódica, como veremos más adelante.

El efecto de estas perturbaciones periódicas puede ser modelado por un término adicional\(F\) en el NSE perturbado de acuerdo con la Ecuación (3.5.1)

\[F(A, A^*, z) = j \xi \sum_{n = -\infty}^{\infty} \delta (z - nz_A) A(z,t). \nonumber \]

La patada periódica del solitón conduce al derramamiento de energía en modos continuos de acuerdo con la Ecuación (3.5.43)

\[\dfrac{\partial}{\partial z} g(k) = jk_s (1 + k^2)g(k) + \langle \text{f}_k^{(+)} \text{F} (A, A^*, z) e^{jk_s z} \rangle. \nonumber \]

\[\begin{align*} \langle \text{f}_{k}^{(+)} \text{F} (A, A^*, z) e^{jk_s z} \rangle &= j \xi \sum_{n = -\infty}^{\infty} \delta (z - nz_A) \dfrac{1}{2} \cdot \int_{-\infty}^{+\infty} \dfrac{1}{\pi (k^2 + 1)^2} e^{jkx} \left (\begin{matrix} (k + j \tanh x)^2 \\ -\text{sech}^2 x \end{matrix} \right ) \cdot \left ( \begin{matrix} 1 \\ 1 \end{matrix} \right ) A_0 \text{sech} x\ dx\\[4pt] &=j \xi \sum_{n = -\infty}^{\infty} \delta (z - n z_A) \cdot \int_{-\infty}^{+\infty} \dfrac{A_0}{2\pi (k^2 + 1)^2} e^{jkx} (k^2 + 2jk \tanh x - 1) \cdot \text{sech} x\ dx \end{align*} \nonumber \]

Nota,\(\tfrac{d}{dx} \text{sech} x = -\text{sech} x \tanh x\), y por lo tanto

\[\begin{align*} \langle \text{f}_k^{(+)} \text{F} (A, A^*, z) e^{jz} \rangle &= -j \xi \sum_{n = -\infty}^{\infty} \delta (z - nz_A) \cdot \int_{-\infty}^{+\infty} \dfrac{A_0}{2\pi (k^2 + 1)} e^{jkx} \cdot \text{sech} x dx \\&= -j \xi \sum_{n = -\infty}^{\infty} \delta (z - nz_A) \dfrac{A_0}{4(k^2 + 1)} \text{sech} (\dfrac{\pi k}{2}). \end{align*} \nonumber \]

Usando\(\sum_{n = -\infty}^{\infty} \delta (z - nz_A) = \dfrac{1}{z_A} \sum_{m = -\infty}^{\infty} e^{jm \tfrac{2\pi}{z_A} z}\) obtenemos

\[\dfrac{\partial}{\partial z} g(k) = jk_s (1 + k^2) g(k) - j \dfrac{\xi}{z_A} \sum_{m =-\infty}^{\infty} e^{jm \tfrac{2\pi}{z_A} z} \dfrac{A_0}{4(k^2 + 1)} \text{sech} \left(\dfrac{\pi k}{2}\right).\label{eq3.6.6} \]

La ecuación\ ref {eq3.6.6} es una ecuación diferencial lineal con coeficientes constantes para las amplitudes continuas\(g(k)\), que puede resolverse por variación de constantes con el ansatz

\[g(k,z) = C(k, z) e^{jk_s (1 + k^2) z}, \nonumber \]

y condiciones iniciales\(C(z = 0) = 0\), obtenemos

\[\dfrac{\partial}{\partial z} C(k, z) = -j \dfrac{\xi}{z_A} \sum_{m = -\infty}^{\infty} \dfrac{A_0}{4(k^2+1)} \text{sech} \left(\dfrac{\pi k}{2}\right) e^{-j(k_s (1 + k^2) - m \tfrac{2\pi}{z_A} z)}, \nonumber \]

o

\[\begin{align*} C(k,z) &= -j \dfrac{\xi}{z_A} \dfrac{A_0}{4(k^2+1)} \text{sech} \left(\dfrac{\pi k}{2} \right) \cdot \sum_{m = -\infty}^{\infty} \int_0^z e^{j(-k_s (1 + k^2) + m \tfrac{2\pi}{z_A})z} dz \\[4pt] &= -j\dfrac{\xi}{z_A} \dfrac{A_0}{4(k^2+1)} \text{sech} \left(\dfrac{\pi k}{2}\right) \cdot \sum_{m = -\infty}^{\infty} \dfrac{e^{j(-k_s (1 + k^2) + m \tfrac{2\pi}{z_A})z} - 1}{m\tfrac{2\pi}{z_A} - k_s (1 + k^2)}. \end{align*} \nonumber \]

Hay un denominador resonante, que explota a ciertas frecuencias normalizadas\(k_m\) para\(z \to \infty\) Esas frecuencias están dadas por

\[m \dfrac{2\pi}{z_A} - k_s (1 + k_m^2) = 0 \nonumber \]

o

\[ k_m = \pm \sqrt{\dfrac{m\tfrac{2\pi}{z_A}}{k_s} - 1}. \nonumber \]

Eliminando la normalización por ajuste\(k = \omega \tau\),\(k_s =|D_2|/\tau^2\) e introduciendo el desplazamiento de fase no lineal del solitón adquirido durante un período de la perturbación\(\phi_0 = k_s z_A\), obtenemos una fórmula práctica para la ubicación de las bandas laterales resonantes

\[\omega_m = \pm \dfrac{1}{\tau} \sqrt{\dfrac{2m \pi}{\phi_0} - 1}, \nonumber \]

y los coeficientes

\[C(\omega, z) = -j \dfrac{\xi}{z_A} \dfrac{A_0}{4((\omega \tau)^2 + 1)} \text{sech} (\dfrac{\pi \omega \tau}{2}) \cdot \sum_{m = -\infty}^{\infty} z_A \dfrac{e^{j(-k_s (1 + (\omega \tau)^2) + m \tfrac{2\pi}{z_A})z} - 1}{2 \pi m - \phi_0 (1 + (\omega \tau)^2)}. \nonumber \]

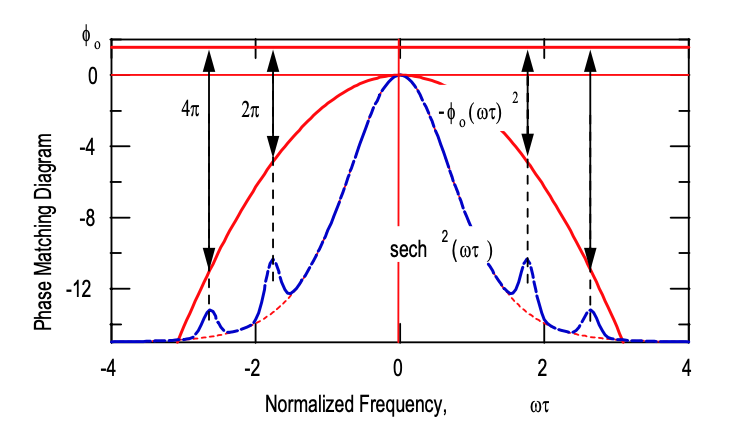
Los coeficientes permanecen limitados para frecuencias no iguales a la condición resonante y crecen linealmente con\(z_A\), en resonancia, lo que conduce a una destrucción del pulso. Para estabilizar el solitón frente a este crecimiento de bandas laterales resonantes, las frecuencias resonantes tienen que permanecer fuera del espectro del solitón, ver Figura 3.10, que alimenta el continuo, i.e\(\omega_m \gg \tfrac{1}{\tau}\). Esta condición solo se cumple si\(\phi_0 \ll \dfrac{\pi}{4}\). Esta condición requiere que el periodo solitón sea mucho más largo que el periodo de la perturbación. Como ejemplo la Figura 3.10 muestra las bandas laterales resonantes observadas en un láser de fibra. Para los sistemas de comunicación óptica esta condición requiere que la energía del solitón tenga que mantenerse lo suficientemente pequeña, de manera que el período de solitón sea mucho más largo que la distancia entre amplificadores, que constituyen perturbaciones periódicas al solitón. Estas bandas laterales suelen llamarse bandas laterales Kelly, según la persona que primero describió su origen correctamente [30].

Figura 3.10: Phasematching entre solitón y continuo debido a perturbaciones periódicas conduce a la generación de banda lateral resonante. El caso mostrado es para\(\phi_0 = \pi/2\).

Para ilustrar su importancia se discute el espectro observado a partir del sistema láser Ti:zafiro de cavidad larga ilustrado en la Figura 3.11 y descrito con todo detalle en [37]. Debido a la baja tasa de repetición, se acumula una energía de pulso bastante grande en la cavidad, lo que conduce a un gran desplazamiento de fase no lineal por ida y vuelta.

Figura 3.11: Disposición esquemática de una cavidad láser de alta energía de pulso. Todos los espejos sombreados son (espejos de doble chirped) DCMs. La cavidad estándar de 100 MHz con brazos de 45 cm y 95 cm se extiende desde el OC hasta M6 para los brazos cortos y largos respectivamente. La cavidad de paso múltiple (MPC) está encerrada en la caja punteada. La fuente de la bomba es una frecuencia duplicada Nd: Vanadate que produce hasta 10 W a 532 nm [37]. Kowalewicz, A. M., et al. “Generación de pulsos 150-nJ a partir de un\(\ce{Ti:Al2O3}\) oscilador bloqueado con lente Kerr-lens de cavidad de paso múltiple”. Letras Ópticas 28 (2003): 1507-09.

La Figura 3.12 muestra el espectro de la salida del láser. Las bandas laterales de Kelly son claramente visibles. Es este tipo de inestabilidad, la que limita el aumento adicional de la energía de pulso de estos sistemas que operan en el régimen de conformación de pulsos de solitón. La energía se drena desde el pulso principal hacia las bandas laterales, que crecen a expensas del pulso. En algún momento la conformación del pulso se vuelve inestable debido a las condiciones que se discutirán en capítulos posteriores.

Figura 3.12: Espectro modelobloqueado medido con un FWHM de 16.5 nm centrado a 788 nm. Kowalewicz, A. M., et al. “Generación de pulsos 150-nJ a partir de un\(\ce{Ti:Al2O3}\) oscilador bloqueado con lente Kerr-lens de cavidad de paso múltiple”. Letras Ópticas 28 (2003): 1507-09.