5.7: Modelocking activo con desintonización

Hasta el momento, solo consideramos el caso de sincronismo perfecto entre el ida y vuelta del pulso en la cavidad y el modulador externo. Técnicamente, ese sincronismo perfecto no es fácil de lograr. Una forma sería hacer un bloqueo de modo regenerativo, es decir, se detecta una parte de la señal de salida del láser modelocked, la nota de ritmo a la frecuencia de ida y vuelta se filtra del detector y se envía a un amplificador, que acciona el modulador. Este procedimiento impone el sincronismo si la longitud de la cavidad sufre fluctuaciones debido a vibraciones acústicas y expansión térmica.

Sin embargo, es interesante saber qué tan sensible es el sistema contra la desintonización entre el modulador y el resonador. Resulta que se trata de una situación física y matemáticamente rica, que se aplica a muchos otros fenómenos que ocurren en sistemas impulsados externamente, como la transición de flujo laminar a flujo turbulento en hidrodinámica. Esta transición ha desconcertado a los físicos desde hace más de cien años [1]. Durante los últimos 5 a 10 años, Trefethen y otros han presentado un escenario para la transición a la turbulencia [2]. Este modelo no solo da una descripción cuantitativa del tipo de inestabilidad que conduce a una transición de laminar, es decir, dinámica altamente ordenada, a flujo turbulento, es decir, movimiento caótico, sino también una imagen física intuitiva de por qué ocurren las turbulencias. Tal imagen es la base de muchas inestabilidades láser especialmente en sistemas láser sincronizados. Según esta teoría, la turbulencia se debe al fuerte crecimiento transitorio de desviaciones desde un punto estacionario estable del sistema junto con un mecanismo de retroalimentación no lineal. El mecanismo de retroalimentación no lineal conecta parte de la perturbación amplificada de nuevo a la perturbación inicial. Por lo tanto, la perturbación experimenta un fuerte crecimiento repetidamente. Una vez que el crecimiento transitorio es lo suficientemente grande, una ligera perturbación desde el punto estacionario estable convierte al sistema en turbulencia. Pequeñas perturbaciones están siempre presentes en los sistemas reales en forma de ruido intrínseco del sistema o ruido ambiental y, en simulaciones por computadora, debido a la precisión finita. Las predicciones del análisis de estabilidad linealizado no tienen sentido en tales casos. El láser desintonizado activamente modeloqueado es un excelente ejemplo de dicho sistema, que además se puede estudiar analíticamente. El caso desintonizado solo se ha estudiado experimentalmente [3] [4] o numéricamente [5] hasta el momento. Aquí, consideramos un enfoque analítico. Tenga en cuenta que este tipo de inestabilidad no puede ser detectada por un análisis de estabilidad lineal que es ampliamente utilizado en las teorías láser y que utilizamos en este curso muy a menudo para demostrar la formación estable de pulsos. Hay que ser conscientes de que pueden surgir tales situaciones, donde los resultados de un análisis de estabilidad linealizado tienen una validez muy limitada.

La ecuación de movimiento para la envolvente del pulso en un láser modelokeado activamente con desintonización se puede escribir como

\[T_M \dfrac{\partial A(T, t)}{\partial T} = \left [g(T) - l + D_f \dfrac{\partial^2}{\partial t^2} - M(1 - \cos (\omega_M t)) + T_d \dfrac{\partial}{\partial t} \right ] A(T, t).\label{eq5.7.1} \]

Aquí,\(A(T,t)\) está la envolvente del pulso como antes. Existe el tiempo\(T\) que es de grano grueso en la escala de tiempo del tiempo de ida y vuelta del resonador\(T_R\) y el tiempo\(t\), que resuelve la forma del pulso resultante. La ganancia saturada se denota por\(g(T)\) e izquierda dinámica, porque ya no asumimos que la ganancia y la dinámica de campo alcanzan un estado estacionario eventualmente. La curvatura de las pérdidas intracavitarias en el dominio de la frecuencia, que limitan el ancho de banda del láser, viene dada por\(D_f\) y se deja fija por simplicidad. \(M\)es la profundidad de la modulación de pérdida introducida por el modulador con frecuencia angular\(\omega_M = 2\pi /T_M\), donde\(T_M\) está el periodo del modulador. Tenga en cuenta que Ec. (\(\ref{eq5.7.1}\)) describe el cambio en el pulso entre un periodo de modulación. La desintonización entre el tiempo de ida y vuelta del resonador y el período del modulador es.\(T_d = T_M − T_R\) Esta desintonización significa que el pulso golpea el modulador con algún desplazamiento temporal después de un viaje de ida y vuelta, lo que se puede describir agregando\(T_d \dfrac{\partial}{\partial A} A\) el término en la ecuación maestro.La ganancia saturada\(g\) obedece a ecuación diferencial ordinaria separada

\[\dfrac{\partial g (T)}{\partial T} = - \dfrac{g(T) - g_0}{\tau_L} - g \dfrac{W(T)}{P_L}. \nonumber \]

Como antes,\(g_0\) es la pequeña ganancia de señal debida al bombeo,\(P_L\) la potencia de saturación del medio de ganancia,\(\tau_L\) el tiempo de relajación de ganancia y\(W (T) = \int |A(T,t)|^2\ dt\) la energía de campo total almacenada en la cavidad en el momento\(T\).

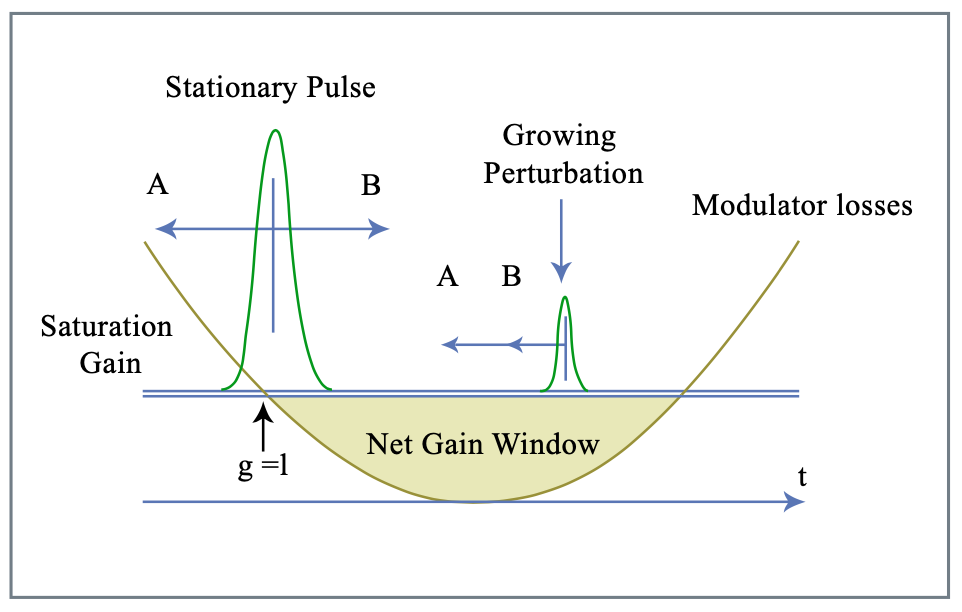
Como antes, esperamos pulsos con un ancho de pulso mucho más corto que el tiempo de ida y vuelta en la cavidad y suponemos que todavía se colocarán en el tiempo cerca de la posición donde el modulador introduce baja pérdida (Figura 5.15), de manera que aún podemos aproximar el coseno por una parábola

\[T_M \dfrac{\partial A}{\partial T} = \left [g - l + D_f \dfrac{\partial ^2}{\partial t^2} - M_s t^2 + T_d \dfrac{\partial}{\partial t} \right ] A.\label{eq5.7.3} \]

Figura 5.15: Dinámica de pulso a la deriva en un láser desintonizado activamente modebloqueado para la situación, donde el período del modulador es mayor que el tiempo de ida y vuelta de la cavidad. El desplazamiento A es causado por la falta de coincidencia entre el tiempo de ida y vuelta de la cavidad y el periodo del modulador. El desplazamiento B se debe a pérdidas desiguales experimentadas por el frente y la parte posterior del pulso en el modulador. La ganancia se satura a un nivel donde un posible pulso estacionario no experimenta ganancia o pérdida neta, lo que abre una ventana de ganancia neta después del pulso. Las perturbaciones dentro de esa ventana se amplifican mientras se desplazan hacia el pulso estacionario. Figura por MIT OCW.

Aquí,\(M_s = M\omega_M^2 /2\) está la curvatura de la modulación de pérdida en el punto de pérdida mínima como antes. Ahora se permite que el tiempo t oscile de\(-\infty\) a\(+\infty\), ya que las pérdidas del modulador aseguran que solo durante el rango físicamente permitido la\(-T_R/2 \ll t \ll T_R/2\) radiación pueda acumularse.

En el caso de desintonización de desaparición, es decir\(T_d = 0\), el operador diferencial en el lado derecho de (\(\ref{eq5.7.3}\)), que genera la dinámica y suele llamarse operador de evolución\(\hat{L}\), corresponde al operador Schrödinger del oscilador armónico. Por lo tanto, es útil introducir a los operadores de creación y aniquilación

\[\hat{a} = \dfrac{1}{\sqrt{2}} \left (\dfrac{\tau_a \partial}{\partial t} + \dfrac{t}{\tau_a} \right ), \hat{a}^{\dagger} = \dfrac{1}{\sqrt{2}} \left (\dfrac{\tau_a \partial}{\partial t} + \dfrac{t}{\tau_a} \right ), \nonumber \]

con\(\tau_a = \sqrt[4]{D_f/M_s}\). El operador de evolución\(\hat{L}\) es entonces dado por

\[\hat{L} = g- l - 2 \sqrt{D_f M_s} \left (\hat{a}^{\dagger} \hat{a} + \dfrac{1}{2} \right )\label{eq5.7.5} \]

y la ecuación de evolución (\(\ref{eq5.7.3}\)) puede escribirse como

\[T_M \dfrac{\partial A}{\partial T} = \hat{L} A. \nonumber \]

En consecuencia, las soluciones propias de este operador de evolución son los Hermite-Gaussians, que ya usamos antes

\[A_n (T, t) = u_n (t) e^{\lambda_n T/ T_M} \nonumber \]

\[u_n(t) = \sqrt{\dfrac{W_n}{2^n \sqrt{\pi} n! \tau_a}} H_n (t/\tau_a) e^{-\tfrac{t^2}{2\tau_a^2}}\label{eq5.7.8} \]

y\(\tau_a\) es el ancho de pulso del gaussiano. (ver Figura 5.16a)

Figura 5.16: Modos propios de orden inferior del sistema linealizado para la desintonización de cero,\(\Delta = 0\), (a) y para una desintonización,\(\Delta = 0.32\), en (b).. Figura por MIT OCW.

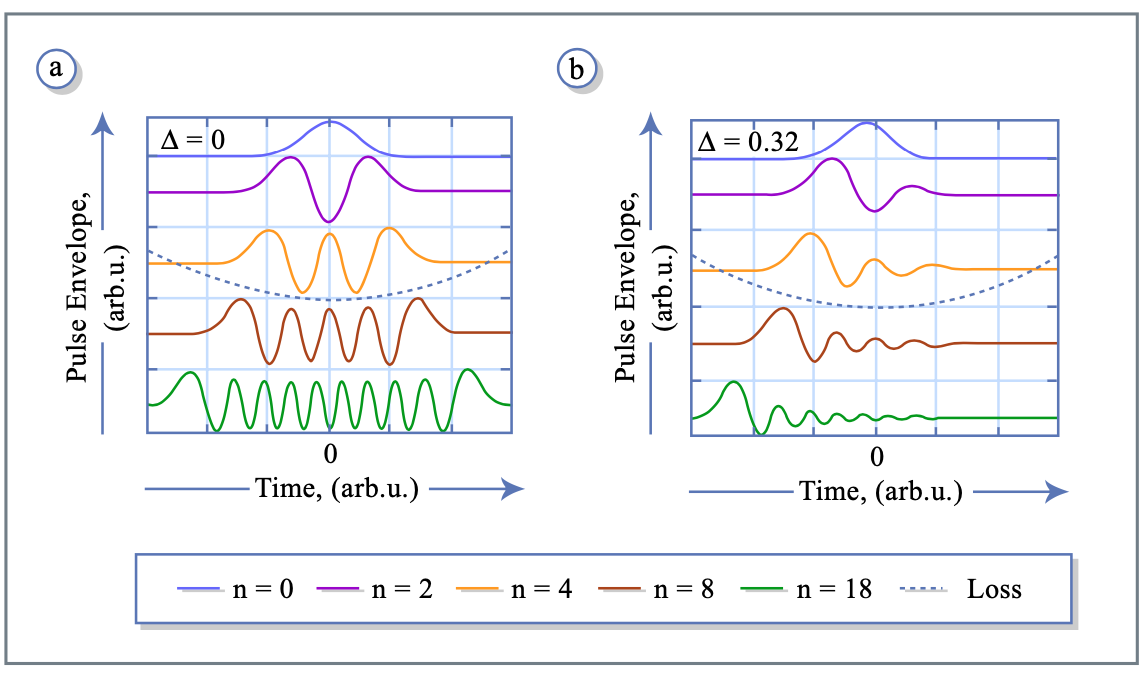
Los modos propios son ortogonales entre sí porque el operador de evolución es hermitiano en este caso.

La ganancia de ida y vuelta del modo propio\(u_n (t)\) viene dada por su valor propio (o en general por la parte real del autovalor) que viene dada por\(\lambda_n = g_n - l - 2 \sqrt{D_f M_s} (n + 0.5)\) donde\(g_n = g_0 \left (1 + \tfrac{W_n}{P_L T_R} \right )^{-1}\), con\(W_n = \int |u_n (t)|^2 dt\). Los valores propios prueban que, para una energía de pulso dada, el modo con\(n = 0\), que llamamos modo tierra, experimenta la mayor ganancia. En consecuencia, el modo tierra saturará la ganancia a un valor tal que\(\lambda_0 = 0\) en estado estacionario y todos los demás modos experimenten pérdida neta,\(\lambda_n < 0\) para\(n > 0\), como se discutió anteriormente. Esta es una situación estable como puede demostrarse rigurosamente mediante un análisis de estabilidad linealizado [6]. Así, el modelocking activo con sincronización perfecta produce pulsos gaussianos con una anchura 1/\(e\) -media del perfil de intensidad dado por\(\tau_a\).

En el caso de la desintonización distinta de cero\(T_d\), la situación se vuelve más compleja. El operador de evolución, (\(\ref{eq5.7.5}\)), cambia a

\[\hat{L}_D = g - l - 2 \sqrt{D_fM_s} \left [(\hat{a}^{\dagger} - \Delta)(\hat{a} + \Delta) + (\dfrac{1}{2} + \Delta^2) \right ] \nonumber \]

con la desintonización normalizada

\[\Delta = \dfrac{1}{2\sqrt{2D_fM_s}} \dfrac{T_d}{\tau_a}.\label{eq5.7.10} \]

Introduciendo los operadores de creación y aniquilación desplazados\(\hat{b} = \hat{a} + \Delta\),\(\hat{b}^{\dagger} = \hat{a}^{\dagger} + \Delta\) y, respectivamente, obtenemos

\[\hat{L}_D = \Delta_g - 2 \sqrt{D_fM_s} (\hat{b}^{\dagger} \hat{b} - 2 \Delta \hat{b}) \nonumber \]

con el exceso de ganancia

\[\Delta g = g - l - 2 \sqrt{D_f M_s} (\dfrac{1}{2} + \Delta^2) \nonumber \]

debido a la desintonización. Tenga en cuenta que el operador de evolución resultante ya no es hermitiano e incluso no normal, es decir\([A, A^{\dagger}] \ne 0\), lo que hace que los modos propios se vuelvan no normales [8]. Sin embargo, es un ejercicio fácil calcular los vectores propios y los valores propios del nuevo operador de evolución en términos de los autoestados de\(\hat{b}^{\dagger} \hat{b}, | l \rangle\), que son los gaussianos hermitas centrados alrededor\(\Delta\). Los vectores propios\(| \varphi_n \rangle\) a\(\hat{L}_D\) son encontrados por el ansatz

\[|\varphi_n \rangle = \sum_{l = 0}^{n} c_l^n |l \rangle, \text{ with } c_{l +1}^{n} = \dfrac{n - l}{2 \Delta \sqrt{l + 1}} c_l^n.\label{eq5.7.13} \]

Los nuevos valores propios son\(\lambda_n = g_n - l - 2\sqrt{D_fM_s} (\Delta^2 + n + 0.5)\). Por inspección, nuevamente es fácil de ver, que los nuevos estados propios forman una base completa en\(L_2 (\mathbb{R})\). Sin embargo, los vectores propios ya no son ortogonales entre sí. Las soluciones propias en función del tiempo se dan como producto de un polinomio hermita y un gaussiano desplazado\(u_n (t) = \langle t | \varphi_n \rangle \sim H_n (t/\tau_a) \exp [-\tfrac{(t - \sqrt{2} \Delta_{\tau_a})^2}{2 \tau_a^2}]\). Nuevamente, un análisis de estabilidad linealizado muestra que el modo tierra, es decir\(|\varphi_0 \rangle\), un gaussiano, es una solución estacionaria estable. Sorprendentemente, el análisis linealizado predice la estabilidad del modo tierra para todos los valores de la desafinación en la modulación parabólica y aproximación de ganancia. Este resultado es incluso inde- pendiente de la dinámica de la ganancia, es decir, la vida útil del estado superior del medio activo, siempre y cuando haya suficiente ganancia para soportar el pulso. Sólo la posición del máximo del modo tierra,\(\sqrt{2} \Delta \cdot \tau_a\), depende de la desintonización normalizada.

La Figura 5.15 resume los resultados obtenidos hasta el momento. En el caso de desafinación, el centro del pulso gaussiano estacionario se desplaza alejándose de la posición de pérdida mínima del modulador. Dado que la ganancia y pérdida neta dentro de una ida y vuelta en la cavidad del láser tiene que ser cero para un pulso estacionario, hay una ventana de ganancia neta larga después del pulso en el caso de desafinación debido a la ganancia excesiva necesaria. La Figura 2 muestra algunas de las funciones propias de orden más bajo resultantes para el caso de una desintonización normalizada\(\Delta = 0\) en (a) y\(\Delta = 0.32\) en (b). Estas funciones propias no son ortogonales como resultado del operador de evolución no normal

Dinámica del láser desintonizado activamente bloqueado en modo

Para conocer la dinámica del sistema, observamos simulaciones por computadora para un\(\ce{Nd:YLF}\) Láser con los parámetros mostrados en la Tabla 5.3 Figuras

Cuadro 5.3: Datos utilizados en las simulaciones de un\(\ce{Nd:YLF}\) láser.

\(E_L = 366 \ \mu J\)	\(g_0 = 0.79\)
\(\tau_L = 450 \ \mu s\)	\(M_s = 2.467 \cdot 10^{17} s^{-2}\)
\(\Omega_g = 1.12 THz\)	\(D_g = 2 \cdot 10^{-26} s^2\)
\(T_R = 4\ ns\)	\(\tau_a = 17 \ ps\)
\(l = 0.025\)	\(\lambda_0 = 1.047\ \mu m\)
\(M = 0.2\)

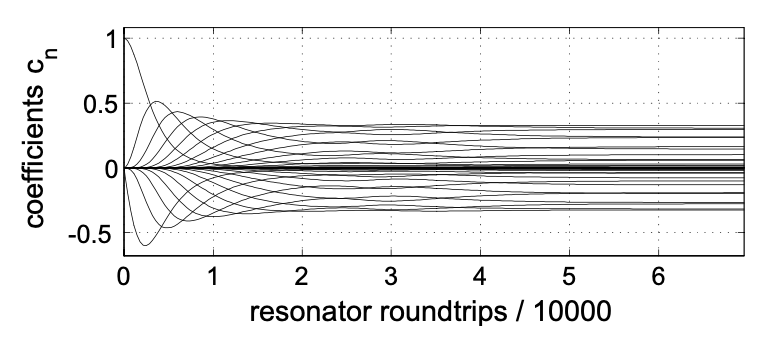
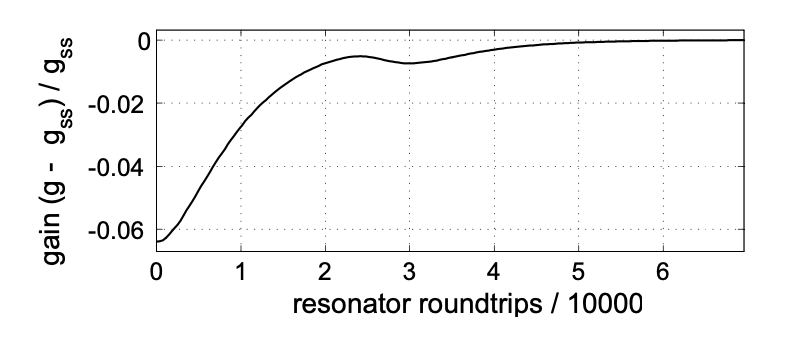
5.17 muestran la evolución temporal del coeficiente cn, cuando la ecuación maestra se descompone en gaussianos hermitas centrados en\(t=0\) según la ecuación (\(\ref{eq5.7.8}\)).

\[A(T, t) = \sum_{n = 0}^{\infty} c_n (T) u_n (t)\nonumber \]

Figura 5.17: Coeficientes de la envolvente en una base ermita-gaussiana, en función de los viajes de ida y vuelta del resonador. La desintonización normalizada es\(\Delta = 3.5\). La simulación se inicia desde el estado estacionario sin desintonizar. La curva que comienza en 1 es el modo tierra. Para describir un pulso desplazado, son necesarios muchos modos.

Las figuras 5.18 y 5.19 muestran la desviación de la ganancia de estado estacionario y la envolvente del pulso en el dominio del tiempo para una desintonización normalizada de\(\Delta = 3.5\).

Figura 5.18: Ganancia en función del número de viajes de ida y vuelta. Cambia a un nivel superior.

Figura 5.19: Evolución temporal de la envoltura de pusle. El pulso cambia lentamente a la nueva posición de equilibrio\(\sqrt{2} \Delta = 4.9\) de acuerdo con la simulación.

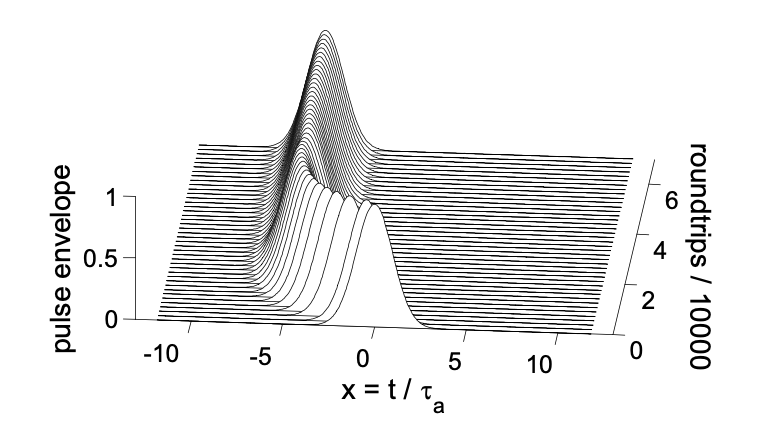
Las figuras 5.20 a 5.22 muestran las mismas cantidades para una desintonización normalizada ligeramente superior de\(\Delta = 4\).

Figura 5.20: Evolución temporal de los coeficientes en una Base Hermita-Gaussiana a una desintonización normalizada de\(\Delta = 4\). Los eventos de interrupción casi peridóicamente cortos del movimiento por lo demás regular pueden reconocerse fácilmente (Comportamiento Intermitente). Durante un período prolongado de tiempo entre tales eventos, el láser se acerca casi a un estado estacionario.

Figura 5.22: Evolución temporal de la envolvente del pulso.

Figura 5.21: Evolución temporal de la desviación respecto a la ganancia en estado casi estacionario.

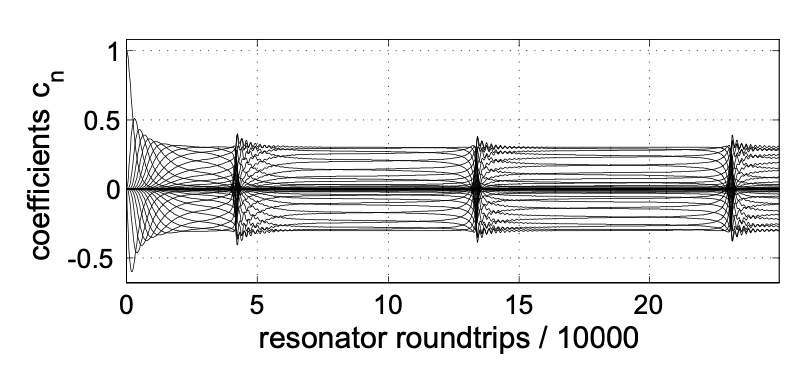
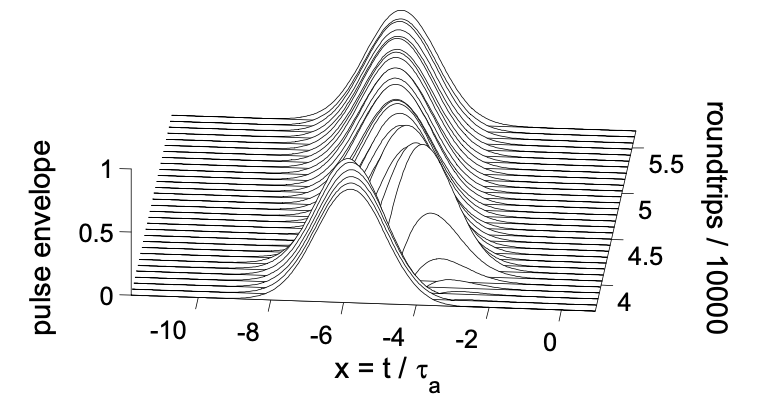
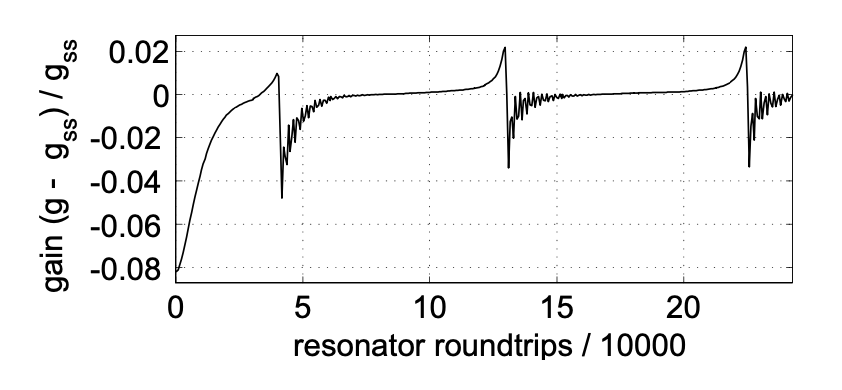
Las imágenes muestran claramente que el sistema ya no se acerca a un estado estacionario, sino que se mantiene turbulento, es decir, la dinámica es caótica.

Sistemas no normales y ganancia transitoria

Para conocer la dinámica de una evolución temporal no normal, consideramos el siguiente sistema bidimensional no normal

\[\dfrac{du}{dt} = Au,\ u(0) = u_0,\ u(t) = e^{At} u_0 \nonumber \]

Figura 5.23: Descomposición de una perturbación inicial en base eigen.

con

\[A = \left (\begin{matrix} -\tfrac{1}{2} & \tfrac{a}{2} \\ 0 & -1 \end{matrix} \right ) \Rightarrow A^{\dagger} = \left (\begin{matrix} -\tfrac{1}{2} & 0 \\ \tfrac{a}{2} & -1 \end{matrix} \right ), [A, A^{\dagger}] = \dfrac{a}{4} \left (\begin{matrix} a & 1 \\ 1 & a \end{matrix} \right ) \ne 0. \nonumber \]

El parámetro\(a\) escala la fuerza de la no normalidad, de manera similar a la desafinación\(\Delta\) en el caso de un láser modelocked o el número de Reynolds en hidrodinámica, donde las ecuaciones linealizadas de Navier-Stokes constituyen un sistema no normal.

Los valores propios y vectores del sistema lineal son

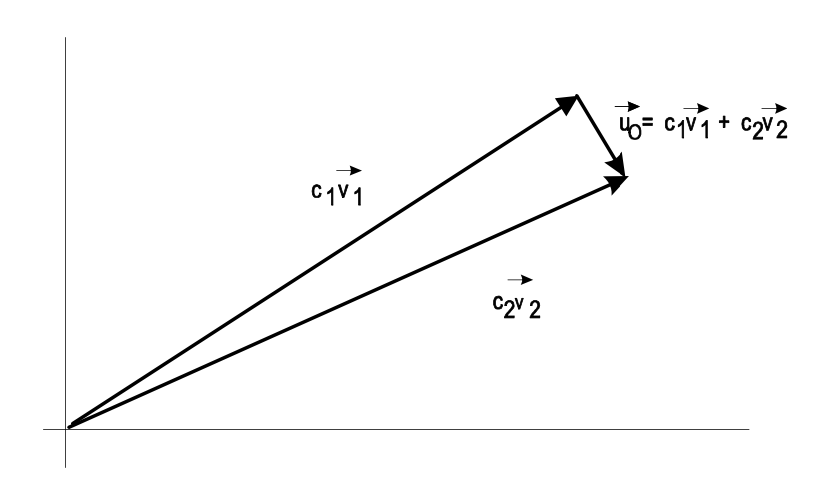
\[\lambda_1 = - \dfrac{1}{2}, v_1 = \left (\begin{matrix} 1 \\ 0 \end{matrix} \right ), \lambda_2 = -1, v_2 = \dfrac{1}{\sqrt{1 + a^2}} \left (\begin{matrix} a \\ -1 \end{matrix} \right ) \nonumber \]

Los vectores propios construyen un sistema completo y cada vector inicial se puede descomponer en esta base. Sin embargo, para grandes a, los dos vectores propios se vuelven cada vez más paralelos, de manera que una descomposición de un pequeño vector inicial casi ortogonal a los vectores base necesita componentes grandes (Figura 5.23)

La solución es

\[u(t) = e^{At} u_0 = c_1 e^{-t/2} \vec{v}_1 + c_2 e^{-t} \vec{v}_2.\nonumber \]

Dado que los valores propios son negativos, ambas contribuciones disminuyen y el sistema es estable. Sin embargo, un componente eigen se descompone dos veces más rápido que el otro. De importancia para nosotros es la ganancia transitoria que el sistema está mostrando debido al hecho de vectores eigen cercanos paralelos. Ambos coeficientes\(c_1\) y\(c_2\) son grandes. Cuando uno de los componentes decae, el otro sigue ahí y el vector resultante

\[u(t \to 2) \approx c_1 e^{-1} \vec{v}_1.\nonumber \]

puede ser mucho mayor que la perturbación inicial durante esta fase transitoria.

Esto es ganancia transitoria. Puede llegar a ser arbitrariamente grande para grande\(a\).

Comportamiento no ormal del láser desintonizado

La no normalidad del operador,\([\hat{L}_D, \hat{L}_D^{\dagger} \sim \Delta\), aumenta con la desintonización. La Figura 5.24 muestra los productos escalares normalizados entre los modos propios para diferentes valores de la desintonización

\[C(m, n) = \left |\dfrac{\langle \varphi_m |\varphi_n \rangle}{\sqrt{\langle \varphi_m |\varphi_m \rangle \langle \varphi_n |\varphi_n \rangle}} \right |. \nonumber \]

Los modos propios son ortogonales para la desintonización de cero. La ortogonalidad se desvanece con una mayor desintonización. La relación de recursión (\(\ref{eq5.7.13}\)) nos dice que la superposición de los nuevos modos propios con el modo tierra aumenta para aumentar la desafinación. Esto corresponde a la paralelización de los modos propios del problema linealizado que conduce a una gran ganancia transitoria,\(|| e^{\hat{L}_D t}||\), en una situación no normal [2]. La Figura 5.24d muestra la ganancia transitoria para una perturbación inicial del modo de tierra estacionaria calculada mediante simulaciones numéricas del sistema linealizado utilizando una expansión del sistema linealizado en términos de estados Fock al operador\(\hat{b}\). Una desafinación normalizada de\(\Delta = 3\) ya conduce a ganancias transitorias para perturbaciones del orden de 106 dentro de 20, 000 viajes de ida y vuelta que conducen a una enorme sensibilidad del sistema contra las perturbaciones. Una solución analítica del sistema linealizado descuidando la saturación de ganancia muestra que la ganancia transitoria escala con la desafinación según\(\exp(2\Delta^2)\). Este fuerte crecimiento súper exponencial con una creciente desintonización determina la dinámica por completo.

Imagen eliminada debido a restricciones de derechos de autor.

Por favor vea:
Kaertner, F. X., et al. “Turbulencia en los Láseres Modo-bloqueados”. Cartas de Revisión Física 82, núm. 22 (mayo de 1999): 4428-4431.

Figura 5.24: Productos escalares de vectores propios en función del índice de vectores propios para los casos\(\Delta = 0\) mostrados en (a),\(\Delta = 1\) en (b) y\(\Delta = 3\) en (c). (d) muestra la ganancia transitoria como función de tiempo para estas desintonizaciones calculadas y para\(\Delta = 2\), a partir de la dinámica del sistema linealizado.

Imagen eliminada debido a restricciones de derechos de autor.

Por favor vea:
Kaertner, F. X., et al. “Turbulencia en los Láseres Modo-bloqueados”. Cartas de Revisión Física 82, núm. 22 (mayo de 1999): 4428-4431.

Figura 5.25: Desintonización crítica obtenida de simulaciones numéricas en función de la velocidad de bombeo normalizada y el tiempo de decaimiento de la cavidad dividido por la vida útil del estado superior. La desintonización crítica es casi independiente de todos los parámetros láser mostrados. La desintonización crítica media es\(\Delta \approx 3.65\).

La Figura 5.25 muestra la superficie de la transición a turbulencia en el espacio pa- rameter de un\(\ce{Nd:YLF}\) láser, es decir, el desintonamiento crítico\(\Delta\), la velocidad de bombeo\(r = g_0/l\) y la relación entre el tiempo de decaimiento de la cavidad\(T_{cav} = T_R/l\) y la vida útil del estado superior\(\tau_L\). En este modelo, no se incluyeron la emisión espontánea.

La transición a la turbulencia siempre ocurre a una desafinación normalizada de aproximadamente la\(\Delta \approx 3.7\) cual da una ganancia transitoria\(\exp(2\Delta^2) = 10^{12}\). Esto significa que ya las incertidumbres del algoritmo de integración numérica se amplifican a una perturbación tan grande como el propio estado estacionario.Para probar que la dinámica del sistema se vuelve realmente caótica, hay que calcular el coeficiente de Liapunov [9]. El coeficiente de Liapunov describe la rapidez con la que los trajectores del espacio de fase se separan entre sí, si comienzan en estrecha proximidad. Se define formalmente de la siguiente manera. Dos trayectorias\(y(t)\) y\(z(t)\) comienzan en las proximidades en\(t = t_0\)

\[||y(t_0) - z(t_0)|| = \epsilon = 10^{-4}. \nonumber \]

Luego, el sistema se ejecuta durante un tiempo determinado\(\Delta t\) y se evalúa la tasa de crecimiento logarítmico, es decir, el coeficiente de Liapunov, de la distancia entre ambas trayectorias utilizando

\[\lambda_0 = \ln \left (\dfrac{||y(t_0 + \Delta t) - z (t_0 + \Delta t) ||}{\epsilon} \right )\label{eq5.7.19} \]

Para la siguiente iteración, la trayectoria\(z(t)\) se vuelve a escalar a lo largo de la distancia entre\(y(t_0 + \Delta t)\) y de\(z(t_0 + \Delta t)\) acuerdo con

\[z(t_1) = y(t_0 + \Delta t) + \epsilon \dfrac{y(t_0 + \Delta t) - z (t_0 + \Delta t)}{||y(t_0 + \Delta t) - z (t_0 + \Delta t) ||}. \nonumber \]

Se calculan los nuevos puntos de las trayectorias\(z (t_1 + \Delta t)\) y\(y (t_1 + \Delta t) = y(t_0 + 2\Delta t)\) se calcula una nueva estimación para el coeficiente\(\lambda_1\) de Liapunov utilizando la Ec. (\(\ref{eq5.7.19}\)) con nuevos índices. Este procedimiento se continúa y el coeficiente de Liapunov se define como el promedio de todas las aproximaciones a lo largo de una iteración lo suficientemente larga, de manera que sus cambios están por debajo de un cierto error enlazado de iteración a iteración.

\[\lambda = \dfrac{1}{N} \sum_{n = 0}^{N} \lambda_n \nonumber \]

La Figura 5.26 muestra el coeficiente de Liapunov del\(\ce{Nd:YLF}\) láser discutido anteriormente, en función de la desintonización normalizada. Cuando el coeficiente de Liapunov se vuelve positivo, es decir, el sistema se vuelve exponencialmente sensible a pequeños cambios en las condiciones iniciales, el sistema se llama caótico. La gráfica indica claramente que la dinámica es caótica por encima de una desintonización crítica de aproximadamente\(\Delta_c \approx 3.7\).

Imagen eliminada debido a restricciones de derechos de autor.

Por favor vea:
Kaertner, F. X., et al. “Turbulencia en los Láseres Modo-bloqueados”. Cartas de Revisión Física 82, núm. 22 (mayo de 1999): 4428-4431.

Figura 5.26: Coeficiente de Liapunov sobre desintonización normalizada.

En el régimen turbulento, el sistema no alcanza un estado estacionario, debido a que no es interrumpido periódicamente por un nuevo pulso creado a partir de la ventana de ganancia neta, ver Figura 5.15, siguiendo el pulso para desintonización positiva. Este pulso satura la ganancia y el pulso de estado estacionario casi formado se destruye y finalmente se reemplaza por uno nuevo. La saturación de ganancia proporciona el mecanismo de retroalimentación no lineal, que vuelve a perturbar fuertemente el sistema, una vez que crece una fuerte perturbación debido al mecanismo de amplificación lineal transitoria.

La desafinación crítica se reduce si se toman en cuenta fuentes de ruido adicionales, como el ruido de emisión espontánea del amplificador láser y las fuentes de ruido técnico. Sin embargo, debido al crecimiento súper exponencial, la desafinación crítica no dependerá fuertemente de la fuerza de las fuentes de ruido. Si se incluye el ruido de emisión espontánea en la simulación, se obtiene la misma forma para el desintonizado crítico que en la Figura 5.25, sin embargo el desintonizado crítico se reduce a aproximadamente\(\Delta_c \approx 2\). Tenga en cuenta que esta desintonización crítica es muy insensible a cualquier otro cambio en los parámetros del sistema. Por lo tanto, uno puede esperar que los láseres bloqueados de modo activo sin retroalimentación regenerativa funcionen inestables en una desafinación real, see (\(\ref{eq5.7.10}\)) dado por

\[T_d = 4\sqrt{2D_f M_s} \tau_a \nonumber \]

Para el\(\ce{Nd:YLF}\) láser anterior, el uso de los valores de la Tabla 5.3 da como resultado una precisión relativa de la frecuencia de modulación de

\[\dfrac{T_d}{T_R} = 1.7 \cdot 10^{-6} \nonumber \]

El valor derivado para la estabilidad de frecuencia se puede lograr y mantener fácilmente con modernos sintetizadores de microondas. Sin embargo, esto requiere que la longitud de la cavidad\(\ce{Nd:YLF}\) del láser también sea estable a este límite. Tenga en cuenta que el coeficiente de expansión térmica para el acero es\(1.6 \cdot 10^{-5}/K\).

Bibliografía

[1] Señor Kelvin, Philos. Mag. 24, 188 (1887); A. Sommerfeld, Int. Mathem. Kongr. Rom 1908, Vol. III, S. 116; W. M. F. Orr, Proc. Irish Acad. 27, (1907).

[2] L. Trefethen, A. Trefethen, S. C. Reddy u. T. Driscol, Ciencia 261, 578 (1993); S. C. Reddy, D. Henningson, J. Fluid Mech. 252, 209 (1993); Phys. Fluidos 6, 1396 (1994); S. Reddy et al., SIAM J. Appl. Matemáticas. 53; 15 (1993); T. Gebhardt y S. Grossmann, Phys. Rev. E 50, 3705 (1994).

[3] H. J. Eichler, Opt. Comm. 56, 351 (1986). H. J. Eichler, I. G. Koltchanov y B. Liu, Appl. Phys. B 61, 81 (1995).

[4] U. Morgner y F. Mitschke, Phys. Rev.A54, 3149 (1997).

[5] H. J. Eichler, I. G. Koltchanov y B. Liu, Appl. Phys. B 61, 81 - 88 (1995).

[6] H. A. Haus, IEEE JQE 11, 323 (1975).

[7] H. A. Haus, D. J. Jones, E. P. Ippen y W. S. Wong, Journal of Light- wave Technology, 14, 622 (1996).

[8] G. Bachman y L. Narici,” Análisis Funcional”, Nueva York, Academic Press (1966).

[9] A. Wolf, J. B. Swift, H. L. Swinney y J. A. Vastano, Physica D 16, 285 (1985).