6.1: Bloqueo en modo de absorbedor saturable lento

Debido a la pequeña sección transversal para la emisión estimulada en láseres de estado sólido, las energías de pulso intracavitario típicas son mucho más pequeñas que la energía de saturación de la ganancia. Por lo tanto, descuidamos el efecto de la saturación de ganancia debido a un pulso sofar, la ganancia sólo se satura con la potencia promedio. Sin embargo, hay medios de ganancia que tienen grandes secciones transversales de ganancia como semiconductores y colorantes, ver Tabla 4.1, y las energías de pulso intracavitario típicas pueden llegar a ser lo suficientemente grandes como para saturar la ganancia considerablemente en una sola pasada. De hecho, es este efecto, el que hizo que el láser de tinte de modo bloqueado fuera tan acertado. El modelo para el bloqueo del modo absorbedor saturable lento tiene que tener en cuenta el cambio de ganancia en el paso de un pulso [1, 2]. A continuación, consideramos un láser modelocked, que experimenta en un solo ida y vuelta una ganancia saturable y un absorbedor saturable lento. En el láser de tinte, ambos medios son tintes con diferentes intensidades de saturación o con diferente enfoque en los chorros de tinte para que la ganancia y pérdida puedan mostrar diferentes energías de saturación. La ecuación de relajación de la ganancia, en el límite de un pulso corto en comparación con su tiempo de relajación, puede aproximarse mediante

\[\dfrac{dg}{dt} = -g \dfrac{|A(t)|^2}{E_L} \nonumber \]

El coeficiente\(E_L\) es la energía de saturación de la ganancia. La integración de la ecuación muestra, que la ganancia se satura con la energía del pulso\(E(t)\)

\[E(t) = \int_{T_{R/2}}^t dt|A(t)|^2 \nonumber \]

al pasar la ganancia

\[g(t) = g_i \exp [-E(t)/E_L] \nonumber \]

donde\(g_i\) es la ganancia inicial de señal pequeña justo antes de la llegada del pulso. Se mantiene una ecuación similar para la pérdida del absorbedor saturable cuya respuesta (pérdida) está representada por\(q(t)\)

\[g(t) = q_0 \exp [-E(t)/E_A] \nonumber \]

donde\(E_A\) está la energía de saturación del absorbedor saturable. Si la pérdida de fondo se denota por\(l\), la ecuación maestra de bloqueo de modo se convierte en

\[\dfrac{1}{T_R} \dfrac{\partial}{\partial T} A = [g_i (\exp (-E(t)/E_L)) A - l A - q_0 \exp (-E(t)/E_A)]A + \dfrac{1}{\Omega_f^2} \dfrac{\partial^2}{\partial t^2} A\label{eq6.1.5} \]

Aquí, hemos reemplazado la acción filtrante de la ganancia\(D_g = \dfrac{1}{\Omega_f^2}\) producida por un filtro fijo separado. Una solución analítica a esta ecuación integrodiferencial se puede obtener con una aproximación: los exponenciales se expanden a segundo orden. Esto es legítimo si el agotamiento poblacional de la ganancia y los medios absorbedor saturables no son excesivos. Considera una de estas expansiones:

\[q_0 \exp (-E(t)/E_A) \approx q_0 [ 1 - (E(t)/E_A) + \dfrac{1}{2} (E(t)/E_A)^2].\label{eq6.1.6} \]

Solo consideramos la ganancia y pérdida saturables y el ancho de banda de ganancia finita. Que la ecuación maestra viene dada por

\[T_R \dfrac{\partial A(T, t)}{\partial T} = \left [ g(t) - q(t) - l + D_f \dfrac{\partial ^2}{\partial t^2} \right ] A(T, t). \nonumber \]

La dispersión del filtro\(D_f = 1/\Omega_f^2\), modela efectivamente el ancho de banda finito del láser, que podría no ser solo debido al ancho de banda de ganancia finita, sino que incluye todos los efectos limitantes de ancho de banda en una aproximación parabólica. Supongamos que el pulso es una función simétrica del tiempo. Entonces el primer poder de la integral da una función antisimétrica del tiempo, su cuadrado es simétrico. Una función antisimétrica que actúa sobre el pulso\(A(t)\) provoca un desplazamiento. De ahí que la solución de estado estacionario no rinda cero para el cambio por pasada, la derivada\(\dfrac{1}{T_R} \dfrac{\partial A}{\partial T}\) debe equipararse a un desplazamiento\(\Delta t\) de tiempo del pulso. Cuando se hace esto se puede confirmar fácilmente que\(A(t) = A_o \text{sech}(t/\tau)\) es una solución de (\(\ref{eq6.1.6}\)) con restricciones en sus coeficientes. Así, estamos buscando una solución de “estado estacionario”\(A(t, T ) = A_o \text{sech}(\tfrac{t}{\tau} + \alpha \tfrac{T}{T_R})\). Tenga en cuenta que α es la fracción del ancho de pulso, el pulso se desplaza en cada ida y vuelta debido a la conformación por pérdida y ganancia. Las restricciones en sus coeficientes se pueden encontrar fácilmente usando las siguientes relaciones para el pulso sech-pulso

\[E(t) = \int_{-T_{R/2}}^t dt |A(t)|^2 = \dfrac{W}{2} \left (1 + \text{tanh} (\dfrac{t}{\tau} + \alpha \dfrac{T}{T_R}) \right ) \nonumber \]

\[E(t)^2 = \left (\dfrac{W}{2} \right )^2 \left (2 + 2 \text{tanh} (\dfrac{t}{\tau} + \alpha \dfrac{T}{T_R}) - \text{sech}^2 (\dfrac{t}{\tau} + \alpha \dfrac{T}{T_R}) \right ) \nonumber \]

\[T_R \dfrac{\partial}{\partial T} A(t, T) = -\alpha \text{tanh} (\dfrac{t}{\tau} + \alpha \dfrac{T}{T_R}) A(t, T) \nonumber \]

\[\dfrac{1}{\Omega_f^2} \dfrac{\partial^2}{\partial t^2} A(t, T) = \dfrac{1}{\Omega_f^2 \tau^2} \left ( 1 - 2 \text{sech}^2 (\dfrac{t}{\tau} + \alpha \dfrac{T}{T_R}) \right ) A(t, T). \nonumber \]

sustituyéndolos en la ecuación maestra (\(\ref{eq6.1.5}\)) y recogiendo los coeficientes frente a las diferentes funciones temporales. El término constante da la ganancia de señal pequeña necesaria

\[g_i \left [1 - \dfrac{W}{2E_L} + \left (\dfrac{W}{2E_L} \right )^2 \right ] = l + q_0 \left [1 - \dfrac{W}{2E_L} + \left (\dfrac{W}{2E_L} \right )^2 \right ] - \dfrac{1}{\Omega_f^2 \tau^2}.\label{eq6.1.12} \]

La constante delante de la función de tanh impar entrega el cambio de tiempo por ida y vuelta

\[\alpha = \dfrac{\Delta}{\tau} = g_i \left [\dfrac{W}{2E_L} - \left (\dfrac{W}{2E_L} \right )^2 \right ]-q_0 \left [\dfrac{W}{2E_L} - \left (\dfrac{W}{2E_L} \right )^2 \right ]. \nonumber \]

Y finalmente la constante frente a la\(\text{sech}^2\) función -determina el ancho de pulso

\[\dfrac{1}{\tau^2} = \dfrac{\Omega_f^2 W^2}{8} \left (\dfrac{q_0}{E_A^2} - \dfrac{g_i}{E_L^2} \right )\label{eq6.1.14} \]

Estas ecuaciones tienen implicaciones importantes. Considere primero la ecuación para el ancho de pulso inverso, (6.14). Para obtener una solución real, el lado derecho tiene que ser positivo. Esto implica que\(q_0/E_A^2 > g_i/E_L^2\). El absorbedor saturable debe saturarse más fácilmente, y, por lo tanto, con mayor fuerza, que el medio de ganancia para abrir una ventana neta de ganancia (Figura 6.2).

Figura 6.2: Dinámica de un modo láser bloqueado con un absorbedor saturable lento.

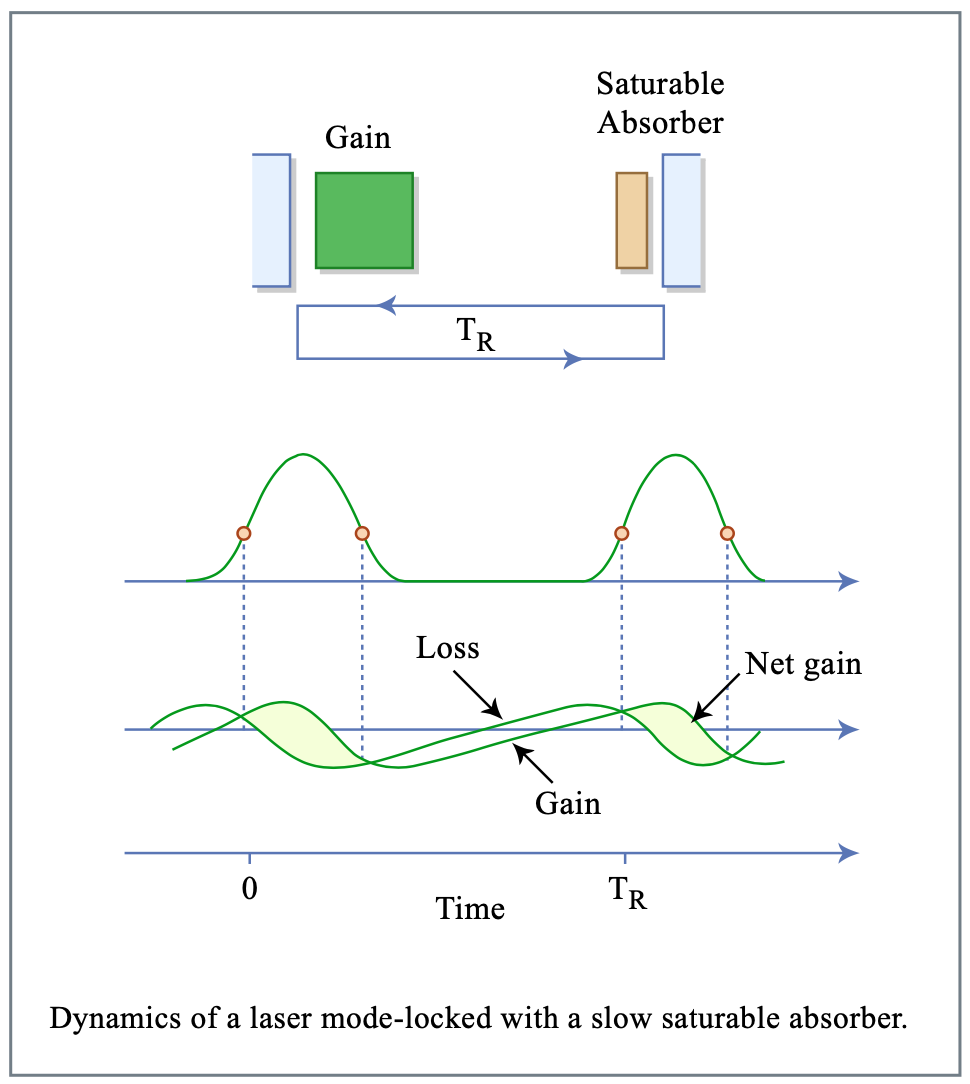
Figura por MIT OCW.

Esto se logró en un sistema de láser de tinte mediante un enfoque más fuerte en el chorro absorbedor-colorante saturable (Reduciendo la energía de saturación para el absorbedor saturable) que en el chorro de tinte de ganancia (que se invirtió, es decir, bombeado ópticamente). La ecuación (\(\ref{eq6.1.12}\)) hace una declaración sobre la ganancia neta antes del paso del pulso. La ganancia neta antes del paso del pulso es

\[g_i - q_0 - l = -\dfrac{1}{\Omega_f^2 \tau^2} + g_i \left [\dfrac{W}{2E_L} - \left (\dfrac{W}{2E_L} \right )^2 \right ] - q_0 \left [\dfrac{W}{2E_A} - \left (\dfrac{W}{2E_A} \right )^2 \right ]. \nonumber \]

Usando condition (\(\ref{eq6.1.14}\)) esto se puede expresar como

\[g_i - g_0 - l = g_i \left [\dfrac{W}{2E_L} \right ] - q_0 \left [ \dfrac{W}{2E_A}\right ] + \dfrac{1}{\Omega_f^2 \tau^2}. \nonumber \]

Esta ganancia es negativa ya que el efecto del absorbedor saturable es mayor que el de la ganancia. Dado que el pulso tiene la misma cola exponencial después del paso que antes, se concluye que la ganancia neta después del paso del pulso es la misma que antes del paso y por lo tanto también negativa. El pulso es estable frente a la acumulación de ruido tanto en su parte delantera como en su parte posterior. Este principio funciona si la relación entre las energías de saturación para el absorbedor saturable y la ganancia\(\chi_P = E_A/E_P\) es muy pequeña. Entonces el ancho de pulso más corto alcanzable con un sistema dado es

\[\tau = \dfrac{4}{\sqrt{q_0} \Omega_f} \dfrac{E_A}{W} > \dfrac{2}{\sqrt{q_0} \Omega_f}. \nonumber \]

El signo mayor viene del hecho de que nuestra teoría se basa en la expansión de los exponenciales, lo cual sólo es cierto para\(\dfrac{W}{2E_A} < 1\). Si la dispersión del filtro\(1/\Omega_f^2\) que determina el ancho de banda del sistema se reemplaza nuevamente por una dispersión de ganancia promedio\(g/\Omega_g^2\) y asumiendo\(g = q_0\). Tenga en cuenta que el principio de modelocking del láser de tinte es muy faszinante debido a que en realidad ninguno de los elementos en el sistema es rápido. Es la interacción entre dos medios lo que abre una ventana corta en el tiempo en la escala de femtosegundos. Los propios medios solo tienen que ser lo suficientemente rápidos como para recuperarse completamente entre un viaje de ida y vuelta, es decir, en una escala de tiempo de nanosegundos.

En los últimos quince años, el láser de tinte ha sido reemplazado en gran medida por láseres de estado sólido, que ofrecen aún más ancho de banda que los tintes y están encima de eso mucho más fáciles de manejar porque no muestran degradación con el tiempo. Con él surgió la necesidad de un principio de bloqueo de modo diferente, ya que la energía de saturación de estos medios láser de estado sólido de banda ancha son mucho mayores que las típicas energías de pulso intracavitario. El absorbedor tiene que abrir y cerrar la ventana de ganancia neta.