6.2: Bloqueo rápido del modo del absorbedor saturable
- Page ID
- 84820
La dinámica de un modelokeado láser con un absorbedor saturable rápido vuelve a estar cubierta por la ecuación maestra (5.1.21) [3]. Ahora, las pérdidas\(q\) reaccionan instantáneamente sobre la intensidad o potencia\(P(t) = |A(t)|^2\) del campo
\[q(A) = \dfrac{q_0}{1 + \tfrac{|A|^2}{P_A}},\label{eq6.2.1} \]
donde\(P_A\) está el poder de saturación del absorbedor. No hay solución analítica de la ecuación maestra (5.1.21) con la respuesta del absorbedor (\(\ref{eq6.2.1}\)). Por lo tanto, hacemos expansiones en la respuesta del absorbedor para obtener una visión analítica. Si el absorbedor no está saturado, podemos ampliar la respuesta (\(\ref{eq6.2.1}\)) para pequeñas intensidades
\[q(A) = q_0 - \gamma |A|^2,\label{eq6.2.2} \]
con el coeficiente de modulación del absorbedor saturable\(\gamma = q_0/P_A\). La pérdida constante de insaturación\(q_0\) puede ser absorbida en las pérdidas\(l_0 = l + q_0\). La ecuación maestra resultante es, véase también la Figura 6.3
\[T_R \dfrac{\partial A(T, t)}{\partial T} = \left [g - l_0 + D_f \dfrac{\partial^2}{\partial t^2} + \gamma |A|^2 + j D_2 \dfrac{\partial^2}{\partial t^2} - j \delta |A|^2 \right ] A(T, t).\label{eq6.2.3} \]
Imagen eliminada debido a restricciones de derechos de autor. Por favor, consulte: Keller, U., Ultrafast Laser Physics, Institute of Quantum Electronics, Swiss Federal Institute of Technology, ETH Hönggerberg—HPT, CH-8093 Zurich, Suiza.
Figura 6.3: Representación esquemática de la ecuación maestra para un láser pasivamente modelado con un absorbedor saturable rápido.
La ecuación (\(\ref{eq6.2.3}\)) es una ecuación generalizada de Ginzburg-Landau bien conocida por la superconductividad con un colector de solución bastante complejo.
Sin GDD y SPM
Consideramos primero la situación sin SPM y GDD, i.e.\(D_2 = \delta =0\)
\[T_R \dfrac{\partial A(T, t)}{\partial T} = \left [g - l_0 + D_f \dfrac{\partial ^2}{\partial t^2} + \gamma |A|^2 \right ] A (T, t).\label{eq6.2.4} \]
Hasta la unidad imaginaria, esta ecuación sigue siendo muy similar a la NSE. Para encontrar la forma y el ancho final del pulso, buscamos la solución estacionaria
\[T_R \dfrac{\partial A_s (T, t)}{\partial T} = 0.\label{eq6.2.5} \]
Como la ecuación es similar a la NSE, intentamos lo siguiente ansatz
\[A_s (T, t) = A_s (t) = A_0 \text{sech} \left (\dfrac{t}{\tau} \right ). \nonumber \]
Tenga en cuenta que hay
\[\dfrac{d}{dx} \text{sech} x = - \text{tanh} x\ \text{sech} x, \nonumber \]
\[\begin{array} {rcl} {\dfrac{d^2}{dx^2} \text{sech} x} & = & {\text{tanh}^2 x\ \text{sech} x - \text{sech}^3 x,} \\ {} & = & {(\text{sech} x - 2 \text{sech}^3 x).} \end{array} \nonumber \]
La sustitución de ansatz (\(\ref{eq6.2.5}\)) en la ecuación maestra (\(\ref{eq6.2.4}\)), asumiendo el estado estacionario, da como resultado
\[0 = \left [(g - l_0) + \dfrac{D_f}{\tau^2} \left [1 - 2 \text{sech}^2 \left (\dfrac{t}{\tau} \right ) \right ] + \gamma |A_0|^2 \text{sech}^2 \left (\dfrac{t}{\tau} \right ) \right ] \cdot A_0 \text{sech} \left (\dfrac{t}{\tau} \right ). \nonumber \]
La comparación de los coeficientes con las\(\text{sech}^3\) expresiones\(\text{sech}\) - y -da como resultado las condiciones para la intensidad de pico de pulso y el ancho de pulso\(\tau\) y para la ganancia saturada
\[\dfrac{D_f}{\tau^2} = \dfrac{1}{2} \gamma |A_0|^2,\label{eq6.2.10} \]
\[g = l_0 - \dfrac{D_f}{\tau^2}\label{eq6.2.11} \]
De la Eq. (\(\ref{eq6.2.10}\)) y con la energía de pulso de un pulso sech, véase la Ec. (3.3.6),\(W = 2|A_0|^2 \tau\),
\[\tau = \dfrac{4D_f}{\gamma W}.\label{eq6.2.12} \]
La ecuación (\(\ref{eq6.2.12}\)) es bastante similar al ancho del solitón con la excepción de que los efectos conservadores de conformación de pulso GDD y SPM son reemplazados por dispersión de ganancia y absorción saturable. El desplazamiento de fase del solitón por ida y vuelta se sustituye por la diferencia entre la ganancia saturada y la pérdida en la Ecuación (\(\ref{eq6.2.12}\)). Es interesante echar un vistazo más de cerca a cómo se produce la diferencia entre ganancia y pérdida\(\tfrac{D_f}{\tau^2}\) por ida y vuelta. De la ecuación maestra (\(\ref{eq6.2.4}\)) podemos derivar una ecuación de movimiento para la energía del pulso de acuerdo con
\[T_R \dfrac{\partial W(T)}{\partial T} = T_R \dfrac{\partial}{\partial T} \int_{-\infty}^{\infty} |A(T, t)|^2 \ dt \nonumber \]
\[= T_R \int_{-\infty}^{\infty} \left [A(T, t) * \dfrac{\partial}{\partial T} A(T, t) + c.c. \right ] \ dt\label{eq6.2.14} \]
\[= 2G (g_s, W) W, \nonumber \]
donde\(G\) está la ganancia neta de energía por ida y vuelta, que desaparece cuando se alcanza el estado estacionario [3]. Sustitución de la ecuación maestra en (\(\ref{eq6.2.14}\)) con
\[\int_{-\infty}^{\infty} (\text{sech}^2 x) dx = 2, \nonumber \]
\[\int_{-\infty}^{\infty} (\text{sech}^4 x) dx = \dfrac{4}{3}, \nonumber \]
\[-\int_{-\infty}^{\infty} \dfrac{d^2}{dx^2} (\text{sech} x) dx = \int_{-\infty}^{\infty} \left (\dfrac{d}{dx} \text{sech} x \right )^2 dx = \dfrac{2}{3}. \nonumber \]
resultados en
\[G(g_s, W) = g_s - l_0 - \dfrac{D_f}{3\tau^2} + \dfrac{2}{3} \gamma |A_0|^2\label{eq6.2.19} \]
\[ = g_s - l_0 + \dfrac{1}{2} \gamma |A_0|^2 = g_s - l_0 + \dfrac{D_f}{\tau^2} = 0\label{eq6.2.20} \]
con la ganancia saturada
\[g_s (W) = \dfrac{g_0}{1 + \tfrac{W}{P_L T_R}} \nonumber \]
La ecuación (\(\ref{eq6.2.20}\)) junto con (\(\ref{eq6.2.12}\)) determina la energía del pulso
\[\begin{array} {rcl} {g_s(W)} & = & {\dfrac{g_0}{1 + \tfrac{W}{P_L T_R} = l_0 - \dfrac{D_f}{\tau^2}} \\ {} & = & {l_0 - \dfrac{(\gamma W)^2}{16D_g}} \end{array} \nonumber \]
La Figura 6.4 muestra la variación dependiente del tiempo de ganancia y pérdida en un modelode láser bloqueado con un absorbedor saturable rápido en una escala de tiempo normalizada Aquí, asumimos que el absorbedor se satura linealmente con intensidad hasta un valor máximo\(q_0 = \gamma A_0^2\). Si esta absorción saturable máxima es completamente explotada ver Figura 6.5.El ancho mínimo de pulso alcanzable con una absorción saturable dada\(q0\) resulta de la Ec. (\(\ref{eq6.2.10}\))
\[\dfrac{D_f}{\tau^2} = \dfrac{q_0}{2}, \nonumber \]
ser
\[\tau = \sqrt{\dfrac{2}{q_0}} \dfrac{1}{\Omega_f}.\label{6.2.24} \]
Imagen eliminada debido a restricciones de derechos de autor. Por favor vea: Kartner, F. X., y U. Keller. “Estabilización de pulsos similares a solitones con un absorbedor saturable lento”. Letras Ópticas 20 (1990): 16-19.
Figura 6.4: Ganancia y pérdida en un láser pasivamente modelado usando un absorbedor saturable rápido en una escala de tiempo normalizada\(x = t/\tau\). Se supone que el absorbedor se satura linealmente con intensidad según\(q(A) = q_0 (1 - \tfrac{|A|^2}{A_0^2})\).
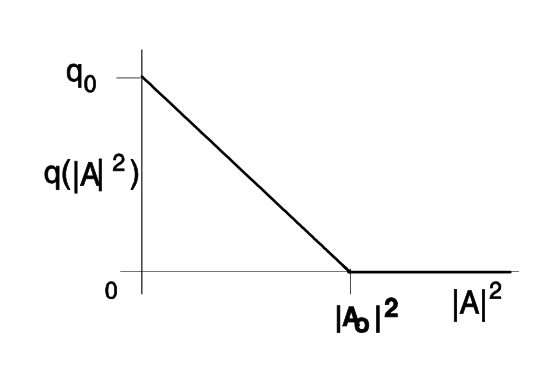
Tenga en cuenta que en contraste con el modelocking activo, ahora el ancho de pulso alcanzable se está escalando con el ancho de banda de ganancia inversa, lo que da pulsos mucho más cortos. La Figura 6.4 puede interpretarse de la siguiente manera: En estado estacionario, la ganancia saturada está por debajo de la pérdida, en aproximadamente la mitad de la pérdida saturable explotada antes y después del pulso. Esto significa, que hay pérdida neta fuera del pulso, lo que mantiene el pulso estable frente al crecimiento de inestabilidades en el borde de ataque y salida del pulso. Si hay una operación estable de modo bloqueado, siempre debe haber pérdida neta lejos del pulso, de lo contrario, una señal de onda continua que corre en el pico de la ganancia experimentaría más ganancia que el pulso y se rompería. De la Eq. (\(\ref{eq6.2.19}\)) sigue, que un tercio de la pérdida saturable explotada se agota durante la saturación del aborber y en realidad solo una sexta parte se usa para superar las pérdidas de filtro debidas al ancho de banda de ganancia finita. Tenga en cuenta que hay un límite para el ancho de pulso de mimio, que se produce, porque la ganancia saturada (\(\ref{eq6.2.11}\)) es\(g_s = l + \dfrac{1}{2} q_0\) y, por lo tanto, de la Ec. (\(\ref{eq6.2.24}\)), si asumimos que el ancho de banda finito del láser está establecido por la ganancia, es decir,\(D_f = D_g = \dfrac{g}{\Omega_g^2}\) obtenemos para\(q_0 \gg 1\)
\[\tau_{\min} = \dfrac{1}{\Omega_g} \nonumber \]
para el modelo de absorbedor linealmente saturante. Esto corresponde al bloqueo de modo sobre el ancho de banda completo del medio de ganancia, ya que para un pulso en forma de sech, el producto tiempo-ancho de banda es 0.315, y por lo tanto,
\[\Delta f_{FWHM} = \dfrac{0.315}{1.76 \cdot \tau_{\min}} = \dfrac{\Omega_g}{1.76 \cdot \pi}. \nonumber \]
A modo de ejemplo, para TI:Zafiro esto corresponde a\(\Omega_g = 270\ THz\),\(\tau_{\min} 3.7\ fs\),\(\tau_{FWHM} = 6.5 \ fs\).
Con GDD y SPM
Después de entender lo que sucede sin GDD y SPM, miramos las soluciones de la ecuación maestra completa (\(\ref{eq6.2.3}\)) con GDD y SPM. Resulta, que existen soluciones de estado estacionario, que son funciones secantes hiperbólicas gorjeadas [4]
\[A_s(T, t) = A_0 \left ( \text{sech} \left ( \dfrac{t}{\tau} \right ) \right )^{1 + j \beta} e^{j\psi T/T_R},\label{eq6.2.26} \]
\[= A_0 \text{sech} \left (\dfrac{t}{\tau}\right ) \exp \left [j\beta \ln \text{sech} \left (\dfrac{t}{\tau}\right ) + j \psi T/T_R \right ]. \nonumber \]
Dónde\(\psi\) está el desplazamiento de fase de ida y vuelta del pulso, que tenemos que permitir. Sólo la intensidad del pulso se vuelve estacionaria. Todavía hay un desplazamiento de fase por ida y vuelta debido a la diferencia entre el grupo y la velocidad de fase (estos efectos ya se han transformado) y los efectos no lineales. Al igual que en la última sección, podemos sustituir este ansatz en la ecuación maestra y comparar coeficientes. Usando las siguientes relaciones
\[\dfrac{d}{dx} (f(x)^b) = bf(x)^{b-1} \dfrac{d}{dx} f(x) \nonumber \]
\[\dfrac{d}{dx} (\text{sech} x)^{(1 +j\beta)} = -(1 + j\beta) \text{tanh} x (\text{sech} x)^{(1 +j\beta)}, \nonumber \]
\[\dfrac{d^2}{dx^2} (\text{sech} x)^{(1 +j\beta)} = ((1 + j \beta)^2 - (2 + 3j\beta - \beta^2) \text{sech}^2 x) (\text{sech} x)^{(1 +j\beta)} \nonumber \]
en la ecuación maestra y comparar los coeficientes con las mismas funciones conduce a dos ecuaciones complejas
\[\dfrac{1}{r^2} (D_f + j D_2)(2+3j\beta - \beta^2) = (\gamma - j \delta)|A_0|^2,\label{eq6.2.31} \]
\[l_0 - \dfrac{(1 + j\beta)^2}{\tau^2} (D_f + j D_2) = g - j \psi.\label{eq6.2.32} \]
Estas ecuaciones son extensiones a las ecuaciones. (\(\ref{eq6.2.11}\)) y (\(\ref{eq6.2.12}\)) y son equivalentes a cuatro ecuaciones reales para el desplazamiento de fase por ida y vuelta\(\psi\), el ancho de pulso\(\tau\), el chirp\(\beta\) y la potencia pico\(|A_0|^2\) o energía de pulso. La parte imaginaria de la Ec. (\(\ref{eq6.2.32}\)) determina únicamente el cambio de fase, que en la mayoría de los casos no es de importancia. La parte real de la Ec. (\(\ref{eq6.2.32}\)) da la ganancia saturada
\[g = l_0 - \dfrac{1 - \beta^2}{\tau^2} D_f + \dfrac{2\beta D_2}{\tau^2}.\label{eq6.2.33} \]
La parte real y la parte imaginaria de la Ec. (\(\ref{eq6.2.31}\)) dar
\[\dfrac{1}{\tau^2} [D_f (2 - \beta^2) - 3\beta D_2] = \gamma |A_0|^2,\label{eq6.2.34} \]
\[\dfrac{1}{\tau^2} [D_2 (2 - \beta^2) + 3\beta D_f] = -\delta |A_0|^2.\label{eq6.2.35} \]
Introducimos la dispersión normalizada\(D_n = D_2/D_f\),, y el ancho de pulso del sistema sin GDD y SPM, es decir, el ancho del sistema modelocked absorbedor puramente saturable,\(\tau_0 = 4D_f/(\gamma W)\). Desviando la ecuación (\(\ref{eq6.2.35}\)) por (\(\ref{eq6.2.34}\)) e introduciendo la no linealidad normalizada\(\delta_n = \delta /\gamma\), obtenemos una ecuación cuadrática para el chirp,
\[\dfrac{D_n (2 - \beta^2) + 3\beta}{(2 - \beta^2) - 3\beta D_n} = -\delta_n,\nonumber \]
o después de algún reodering
\[\dfrac{3\beta}{2 - \beta^2} = \dfrac{\delta_n + D_n}{-1 + \delta_n D_n} \equiv \dfrac{1}{\chi}.\label{eq6.2.36} \]
Tenga en cuenta que\(\chi\) depende únicamente de los parámetros del sistema. Por lo tanto, el chirp es dado por
\[\beta = -\dfrac{3}{2} \chi \pm \sqrt{\left (\dfrac{3}{2} \chi \right )^2 + 2}\label{eq6.2.37} \]
Conociendo el chirp, obtenemos de la Ec. (\(\ref{eq6.2.34}\)) el ancho de impulso
\[\tau = \dfrac{\tau_0}{2} (2 - \beta^2 - 3 \beta D_n), \nonumber \]
que, con la Ec. (\(\ref{eq6.2.36}\)), también se puede escribir como
\[\tau = \dfrac{3\tau_0}{2} \beta (\chi - D_n) \nonumber \]
Para estar físicamente significando completo el ancho del pulso tiene que ser un número positivo, es decir, el producto siempre\(\beta (\chi - D_n)\) tiene que ser mayor que 0, lo que determina la raíz en la Ec. (\(\ref{eq6.2.37}\))
\[\beta = \begin{cases} -\tfrac{3}{2} \chi + \sqrt{(\tfrac{3}{2} \chi)^2 + 2}, & \text{ for } \chi > D_n \\ -\tfrac{3}{2} \chi - \sqrt{(\tfrac{3}{2} \chi)^2 + 2}, & \text{ for } \chi < D_n \end{cases} \nonumber \]
La Figura 6.6 (a, b y d) muestra el chirp resultante, el ancho de pulso y el desplazamiento de fase de ida y vuelta no lineal con respecto a los parámetros del sistema [4] [5]. Un criterio necesario pero no suficiente para la estabilidad de los pulsos es, que debe haber pérdida neta liderando y siguiendo el pulso. De la Eq. (\(\ref{eq6.2.33}\)), obtenemos
\[g_s - l_0 = -\dfrac{1-\beta^2}{\tau^2} D_f + \dfrac{2\beta D_2}{\tau^2} < 0 \nonumber \]
Si definimos el parámetro de estabilidad\(S\)
\[S = 1 - \beta^2 - 2\beta D_n > 0, \nonumber \]
\(S\)tiene que ser mayor que cero, como se muestra en la Figura 6.6 (d).
Imagen eliminada debido a restricciones de derechos de autor.
Por favor vea:
Haus, H. A., J. G. Fujimoto, E. P. Ippen. “Estructura para modeloqueo de pulsos aditivos”. Revista de la Sociedad Óptica de las Américas B 8 (1991): 208.
Figura 6.6: (a) Ancho de pulso, (b) Parámetro Chirp, (c) Ganancia neta después del pulso, lo cual está relacionado con la estabilidad. d) Desplazamiento de fase por pasada. [4]
La Figura 6.6 (a-d) indica que existen esencialmente tres regímenes operativos. Primero, sin GDD y SPM, los pulsos son siempre estables. En segundo lugar, si hay una fuerte conformación de pulso similar a un solitón, es decir,\(\delta_n \gg 1\) y\(-D_n \gg 1\) el chirp siempre es mucho más pequeño que para la dispersión positiva y los pulsos son similares a solitones. Por fin, los pulsos están incluso libres de chirp, si\(\delta_n = -D_n\) se cumple la condición. Entonces la solución es
\[A_s (T, t) = A_0 \left ( \text{sech} \left ( \dfrac{t}{\tau} \right ) \right ) e^{j\psi T/T_R}, \text{ for } \delta_n = -D_n. \nonumber \]
Tenga en cuenta que para esta discusión siempre asumimos un coeficiente SPM positivo. En este régimen también obtenemos los pulsos más cortos directamente del sistema, que pueden ser un factor 2-3 más cortos que por el modelocking de absorbedor saturable puro. Obsérvese que la Figura 6.6 indica incluso pulsos arbitrariamente más cortos si el índice no lineal,\(\delta_n\) es decir, se incrementa aún más. Sin embargo, esto es sólo un artificio de la aproximación lineal del absorbedor saturable, que ahora puede llegar a ser arbitrariamente grande, compare (\(\ref{eq6.2.1}\)) y (\(\ref{eq6.2.2}\)). Como hemos encontrado a partir del análisis del modelo de absorbedor saturable rápido, Figura 6.4, solo una sexta parte de la absorción saturable se utiliza para superar el filtrado de ganancia. Esto es así, porque el absorbedor saturable tiene que dar forma y estabilizar el pulso contra el avance de la radiación cw. Con SPM y GDD esto es relajado. La conformación del pulso se puede hacer solo por SPM y GDD, es decir, la formación de solitones y el absorbedor solo tiene que estabilizar el pulso. Pero entonces toda la absorción saturable se puede agotar para la estabilidad, es decir, seis veces más, lo que permite un cortocircuito de pulso adicional por un factor de aproximadamente\(\sqrt{6} = 2.5\) en una situación de filtro parabólico. Tenga en cuenta, que para un experimentalista un factor de tres es un número grande. Esto nos dice que el límite de 6.5 fs para Ti:zafiro derivado anteriormente del modelo de absorbedor saturable se puede reducir a 2.6 fs incluyendo GDD y SPM, que es aproximadamente un ciclo óptico de 2.7 fs a una longitud de onda central de 800nm. En ese punto todas las aproximaciones, tenemos modo hasta ahora descomponer. Si la cantidad de dispersión negativa se reduce demasiado, es decir, los pulsos se vuelven demasiado cortos, el absorbedor ya no puede mantenerlos estables.
Si hay una fuerte dispersión positiva, los pulsos vuelven a ser estables y largos, pero muy gorjeados. El pulso puede entonces comprimirse externamente, sin embargo no completamente a su límite de transformación, porque estos son pulsos de chirped no linealmente, ver la Ec. (\(\ref{eq6.2.26}\)).
En el caso de una fuerte conformación de pulso similar a un solitón, el absorbedor no tiene que ser realmente rápido, porque el pulso está conformado por GDD y SPM y el absorbedor solo tiene que estabilizar el solitón contra el continuo. A este régimen se le ha denominado bloqueo en modo Soliton.


