7.1: Bloqueo de modo de lente Kerr-Lens (KLM)
- Page ID
- 84907
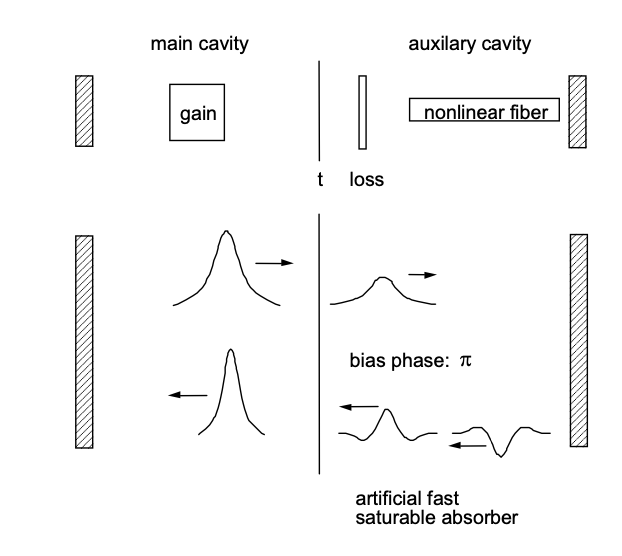
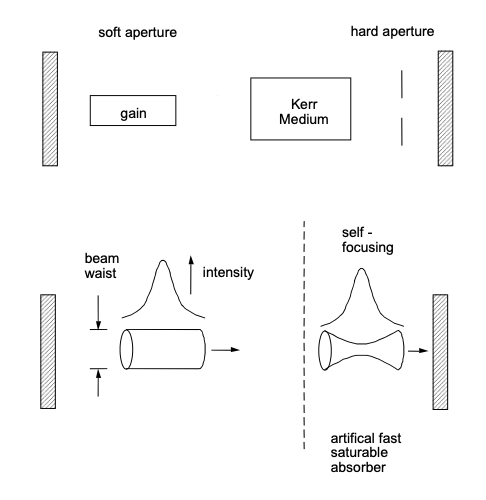
El principio general detrás del bloqueo de modo de lente Kerr-se esboza en la Figura 7.1. Un pulso que se acumula en una cavidad láser que contiene un medio de ganancia y un medio Kerr experimenta no solo modulación de autofase sino también autoenfoque, es decir, lentes no lineales del rayo láser, debido al índice de refracción no lineal del medio Kerr. Un pulso láser espacio-temporal que se propaga a través del medio Kerr tiene un tamaño de modo dependiente del tiempo a medida que intensidades más altas adquieren un enfoque más fuerte. Si se coloca una abertura dura en la posición correcta en la cavidad, se despoja de las alas del pulso, lo que lleva a un acortamiento del pulso. Dicho mecanismo combinado tiene el mismo efecto que un absorbedor saturable. Si se utiliza el efecto Kerr electrónico con tiempo de respuesta de unos femtosegundos o menos, se ha creado un absorbedor saturable rápido. En lugar de un medio Kerr separado y una apertura dura, el medio de ganancia puede actuar tanto como un medio Kerr como una apertura suave (es decir, aumento de ganancia en lugar de absorción saturable). La sensibilidad del tamaño del modo láser en lentes no lineales adicionales se mejora drásticamente si la cavidad se opera cerca del límite de estabilidad de la cavidad. Por lo tanto, es de primordial importancia comprender los rangos de estabilidad de los resonadores láser. Los resonadores láser se entienden mejor en términos de óptica paraxial [11] [12] [14] [13] [15].
Revisión de Óptica Paraxial y Diseño de Resonador Láser
Las soluciones a la ecuación de onda paraxial, que mantienen su forma durante la propagación, son los haces ermita-gaussianos. Dado que consideramos solo los modos transversales fundamentales, estamos tratando con el haz gaussiano
\[U(r, z) = \dfrac{U_o}{q(z)} \exp \left [ -jk \dfrac{r^2}{2q(z)} \right ], \nonumber \]
con el parámetro q complejo\(q = a+jb\) o su inverso
\[\dfrac{1}{q(z)} = \dfrac{1}{R(z)} - j\dfrac{\lambda}{\pi w^2(z)}. \nonumber \]
La intensidad del haz gaussiano\(I(z, r) = |U(r, z)|^2\) expresada en términos de la potencia\(P\) transportada por el haz viene dada por
\[I(r, z) = \dfrac{2P}{\pi w^2(z)} \exp \left [-\dfrac{2r^2}{w^2 (z)} \right ]. \nonumber \]
El uso del parámetro q simplifica la descripción de la propagación del haz gaussiano. En la propagación del espacio libre de\(z_1\) a\(z_2\), la variación del parámetro de haz\(q\) se rige simplemente por
\[q_2 = q_1 + z_2 - z_1, \nonumber \]
donde\(q_2\) y\(q_1\) son los parámetros del haz en\(z_1\) y\(z_2\). Si la cintura del haz, en la que el haz tiene un tamaño de punto mínimo\(w_0\) y un frente de onda plano (\(R = \infty\)), se encuentra en\(z = 0\), las variaciones del tamaño del punto del haz y el radio de curvatura se expresan explícitamente como
\[w(z) = w_o \left [1 + \left (\dfrac{\lambda z}{\pi w_o^2} \right )^2 \right ]^{1/2}, \nonumber \]
y
\[R(z) = z \left [1 + \left (\dfrac{\pi w_o^2}{\lambda z} \right )^2 \right ]. \nonumber \]
La divergencia angular del haz es inversamente proporcional a la cintura del haz. En el campo lejano, la divergencia de medio ángulo viene dada por,
\[\theta = \dfrac{\lambda}{\pi w_o}, \nonumber \]
como se ilustra en la Figura 7.2.
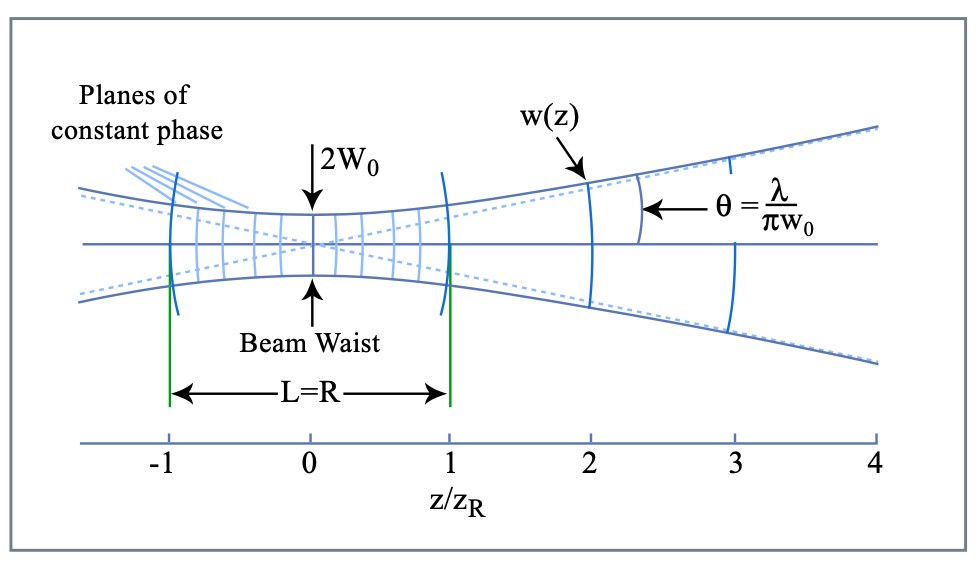
Figura por MIT OCW.
Debido a la difracción, cuanto menor es el tamaño del punto en la cintura del haz, mayor es la divergencia. El rango Rayleigh se define como la distancia desde la cintura sobre la cual se duplica el área de la viga y se puede expresar como
\[z_R = \dfrac{\pi w_o^2}{\lambda}. \nonumber \]
El parámetro confocal del haz gaussiano se define como el doble del rango de Rayleigh
\[b = 2 z_R = \dfrac{2\pi w_o^2}{\lambda}, \nonumber \]
y corresponde a la longitud sobre la que se enfoca el haz. La propagación de haces ermita-gaussianos a través de sistemas ópticos paraxiales puede evaluarse eficientemente utilizando la ley ABCD [11]
\[q_2 = \dfrac{Aq_1 + B}{Cq_1 + D}\label{eq7.1.10} \]
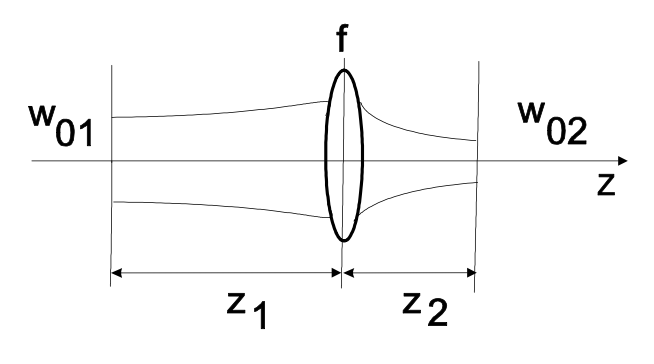
donde\(q_1\) y\(q_2\) son los parámetros del haz en los planos de entrada y salida del sistema óptico o componente. Las matrices ABCD de algunos elementos ópticos se resumen en la Tabla 7.1. Si un haz gaussiano con cintura\(w_{01}\) es enfocado por una lente delgada a una\(z_1\) distancia de la cintura, habrá un nuevo enfoque a distancia
\[z_2 = f + \dfrac{(z_1 - f) f^2}{(z_1 - f)^2 + (\tfrac{\pi w_{01}^2}{\lambda})^2}, \nonumber \]
y una cintura\(w_{02}\)
\[\dfrac{1}{w_{02}^2} = \dfrac{1}{w_{01}^2} \left (1 - \dfrac{z_1}{f} \right )^2 + \dfrac{1}{f^2} \left (\dfrac{\pi w_{01}}{\lambda} \right )^2 \nonumber \]
Resonadores de Dos Espejos
Consideramos los dos resonadores de espejo que se muestran en la Figura 7.4.
| Elemento óptico | Matriz ABCD |
|---|---|
| Distancia de espacio libre\(L\) | \(\left (\begin{matrix} 1 & L \\ 0 & 1 \end{matrix} \right)\) |
| Lente delgada con distancia focal\(f\) | \(\left (\begin{matrix} 1 & 0 \\ -1/f & 1 \end{matrix} \right )\) |
| Espejo bajo ángulo\(\theta\) a eje y radio plano\(R\) sagital | \(\left (\begin{matrix} 1 & 0 \\ \tfrac{-2 \cos \theta}{R} & 1 \end{matrix} \right )\) |
| Espejo bajo ángulo\(\theta\) a eje y radio plano\(R\) tangencial | \(\left (\begin{matrix} 1 & 0 \\ \tfrac{-2}{R\cos \theta} & 1 \end{matrix} \right)\) |
| Placa Brewster bajo ángulo\(\theta\) a eje y grosor\(d\), plano sagital | \(\left (\begin{matrix} 1 & \tfrac{d}{n} \\ 0 & 1 \end{matrix} \right)\) |
| Placa Brewster bajo ángulo\(\theta\) a eje y grosor\(d\), plano tangencial | \(\left (\begin{matrix} 1 & \tfrac{d}{n^3} \\ 0 & 1 \end{matrix} \right)\) |
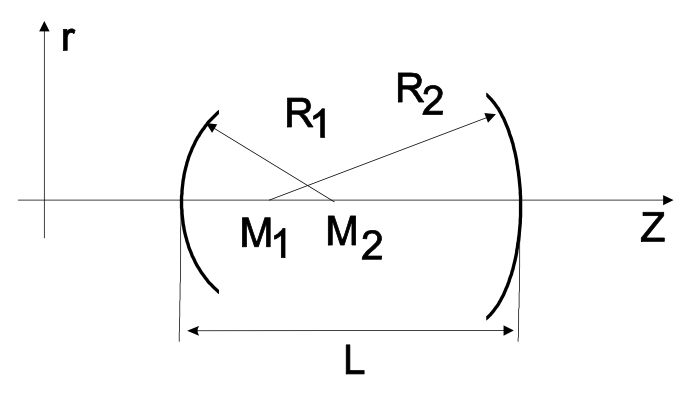
El resonador se puede desplegar para un análisis de matriz ABCD, ver Figura 7.5.
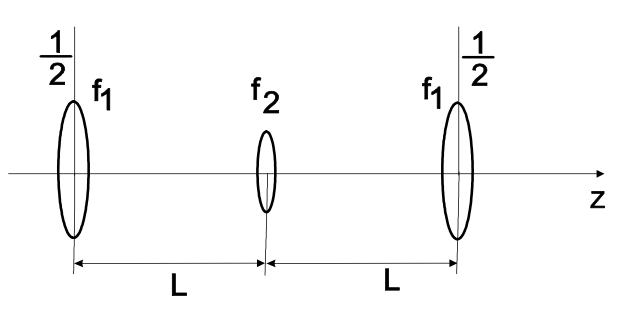
El producto de las matrices ABCD que describen un viaje de ida y vuelta de acuerdo con la Figura 7.5 viene dado por
\[M = \left ( \begin{matrix} 1 & 0 \\ \tfrac{-1}{2f_1} & 1 \end{matrix} \right) \left (\begin{matrix} 1 & L \\ 0 & 1 \end{matrix} \right ) \left (\begin{matrix} 1 & 0 \\ \tfrac{-1}{f_2} & 1 \end{matrix} \right) \left (\begin{matrix} 1 & L \\ 0 & 1 \end{matrix} \right) \left (\begin{matrix} 1 & 0 \\ \tfrac{-1}{2f_1} & 1 \end{matrix} \right) \nonumber \]
dónde\(f_1 = R_1/2\), y\(f_2 = R_2/2\). Para llevar a cabo este producto y formular los criterios de estabilidad de la cavidad, es conveniente utilizar los parámetros de la cavidad\(g_i = 1 - L/R_i\),\(i = 1,2\). La cavidad resultante de ida y vuelta ABCD-matriz se puede escribir en la forma
\[M = \left (\begin{matrix} (2g_1g_2 - 1) & 2g_2L \\ 2g_1(g_1 g_2 - 1)/L & (2g_1g_2 - 1) \end{matrix} \right) = \left (\begin{matrix} A & B \\ C & D \end{matrix} \right). \nonumber \]
Estabilidad del resonador
Las matrices ABCD describen la dinámica de los rayos que se propagan dentro del resonador. Un rayo óptico se caracteriza por el vector\(r = \left ( \begin{matrix} r \\ r' \end{matrix} \right )\), donde\(r\) está la distancia desde el eje óptico y\(r'\) la pendiente del rayo al eje óptico. El resonador es estable si no se escapa ningún rayo después de muchos viajes de ida y vuelta, que es el caso cuando los valores propios de la matriz\(M\) son menores de uno. Ya que tenemos un resonador sin pérdidas, es decir\(\text{det}|M| = 1\), el producto de los valores propios tiene que ser 1 y, por lo tanto, el resonador estable corresponde al caso de un par conjugado complejo de valores propios con una magnitud de 1. La ecuación de valor propio a\(M\) viene dada por
\[\text{det} |M - \lambda \cdot 1| = \text{det} \left |\left (\begin{matrix} (2g_1 g_2 - 1) - \lambda & 2g_2 L \\ 2g_1(g_1g_2 - 1)/L & (2g_1 g_2 - 1) - \lambda \end{matrix} \right ) \right | = 0,\label{eq7.1.15} \]
\[\lambda^2 - 2(2g_1g_2 - 1) \lambda + 1 = 0. \nonumber \]
Los valores propios son
\[\lambda_{1/2} = (2g_1g_2 - 1) \pm \sqrt{(2g_1g_2 - 1)^2 - 1}, \nonumber \]
\[= \begin{cases} \exp (\pm \theta), \text{cosh} \theta = 2g_1 g_2 - 1, & \text{ for } |2g_1 g_2 - 1| > 1 \\ \exp (\pm j \psi), \text{cos} \psi = 2g_1 g_2 - 1, & \text{ for } |2g_1 g_2 - 1| \le 1 \end{cases} \nonumber \]
El caso de un par conjugado complejo con una magnitud unitaria corresponde a un resonador estable. Por lo tanto, el criterio de estabilidad para un resonador estable de dos espejos es
\[|2g_1g_2 - 1| \le 1. \nonumber \]
Los rangos de parámetros estables e inestables están dados por
\[\text{stable : } 0 \le g_1 \cdot g_2 = S \le 1 \nonumber \]
\[\text{unstable : } g_1 g_2 \le 0; \text{ or } g_1 g_2 \ge 1. \nonumber \]
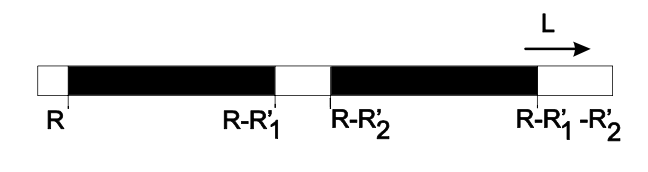
donde\(S = g_1 \cdot g_2\), es el parámetro de estabilidad de la cavidad. El criterio de estabilidad puede ser fácilmente interpretado geométricamente. De importancia son las distancias entre los puntos medios del espejo\(M_i\) y los extremos de la cavidad, es decir\(g_i = (R_i - L)/R_i = -S_i/R_i\), como se muestra en la Figura 7.6.
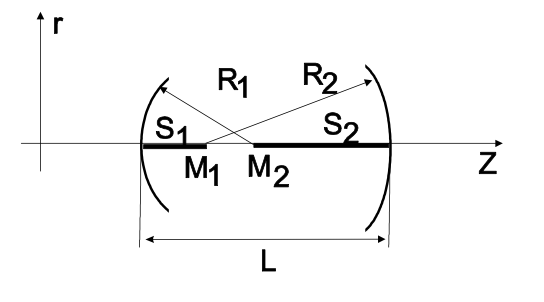
Las siguientes reglas para un resonador estable se pueden derivar de la Figura 7.6 utilizando el criterio de estabilidad expresado en términos de las distancias\(S_i\). Tenga en cuenta que las distancias y radios pueden ser positivos y negativos
\[\text{stable: } 0 \le \dfrac{S_1S_2}{R_1R_2} \le 1. \nonumber \]
Las reglas son:
• Un resonador es estable, si los radios del espejo, dispuestos a lo largo del eje óptico, se superponen.
• Un resonador es inestable, si los radios no se superponen o uno se encuentra dentro del otro.
La Figura 7.7 muestra configuraciones de resonador estables e inestables.
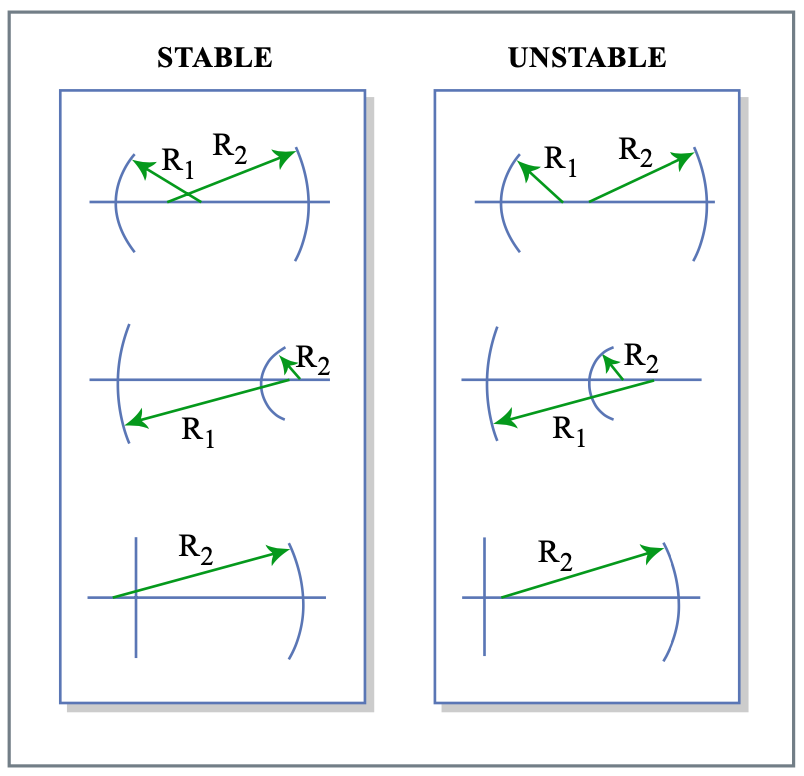
Figura por MIT OCW.
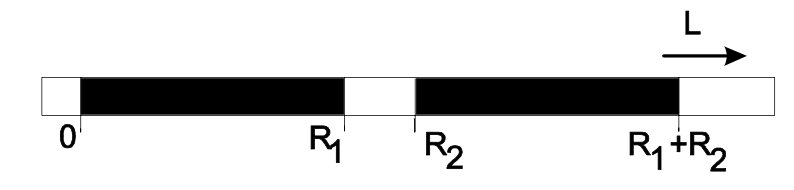
Para un resonador de dos espejos con espejos cóncavos y\(R_1 \le R_2\), obtenemos el diagrama de estabilidad general como se muestra en la Figura 7.8. Hay dos rangos para la distancia del espejo\(L\), dentro de los cuales la cavidad es estable,\(0 \le L \le R_1\) y\(R_2 \le L \le R_1 + R_2\). Es interesante investigar el tamaño del punto en los espejos y el tamaño mínimo de punto en la cavidad en función de la distancia del espejo\(L\).
Características del modo de resonador
Los modos estables del resonador se reproducen después de una ida y vuelta, es decir, desde la Ec. (\(\ref{eq7.1.10}\)) encontramos
\[q_1 = \dfrac{Aq_1 + B}{Cq_1 + D} \nonumber \]
El parámetro q inverso, que está directamente relacionado con la curvatura frontal de fase y el tamaño de punto del haz, está determinado por
\[\left (\dfrac{1}{q} \right )^2 + \dfrac{A - D}{B} \left (\dfrac{1}{q} \right ) + \dfrac{1 - AD}{B^2} = 0. \nonumber \]
La solución es
\[\left (\dfrac{1}{q} \right )_{1/2} = -\dfrac{A - D}{2B} \pm \dfrac{j}{2|B|} \sqrt{(A + D)^2 - 1} \nonumber \]
Si aplicamos esta fórmula a (\(\ref{eq7.1.15}\)), encontramos el tamaño de punto en el espejo 1
\[\left (\dfrac{1}{q} \right )_{1/2} = - \dfrac{j}{2|B|} \sqrt{(A + D)^2 - 1} = -j \dfrac{\lambda}{\pi w_1^2}. \nonumber \]
o
\[w_1^4 = \left ( \dfrac{2\lambda L}{\pi} \right )^2 \dfrac{g_2}{g_1} \dfrac{1}{1 - g_1 g_2}\label{eq7.1.27} \]
\[= \left ( \dfrac{\lambda R_1}{\pi} \right )^2 \dfrac{R_2 - L}{R_1 - L} \left ( \dfrac{L}{R_1 + R_2 - L} \right ). \nonumber \]
Por simetría, encontramos el tamaño de punto en el espejo 3 a través del índice de conmutación 1 y 2:
\[w_2^4 = \left (\dfrac{2\lambda L}{\pi} \right )^2 \dfrac{g_1}{g_2} \dfrac{1}{1 - g_1g_2} \nonumber \]
\[= \left ( \dfrac{\lambda R_2}{\pi} \right )^2 \dfrac{R_1 - L}{R_2 - L} \left ( \dfrac{L}{R_1 + R_2 - L} \right ). \nonumber \]
El foco intracavitario se puede encontrar transformando el haz gaussiano enfocado con la matriz de propagación
\[\begin{array} {rcl} {M} & = & {\left (\begin{matrix} 1 & z_1 \\ 0 & 1 \end{matrix} \right ) \left (\begin{matrix} 1 & 0 \\ \tfrac{-1}{2f_1} & 1 \end{matrix} \right )} \\ {} & = & {\left (\begin{matrix} 1 - \tfrac{z_1}{2f_1} & \tfrac{-1}{2f_1} \\ 0 & 1 \end{matrix} \right ),} \end{array} \nonumber \]
a su nuevo enfoque eligiendo correctamente\(z_1\), ver Figura 7.9.
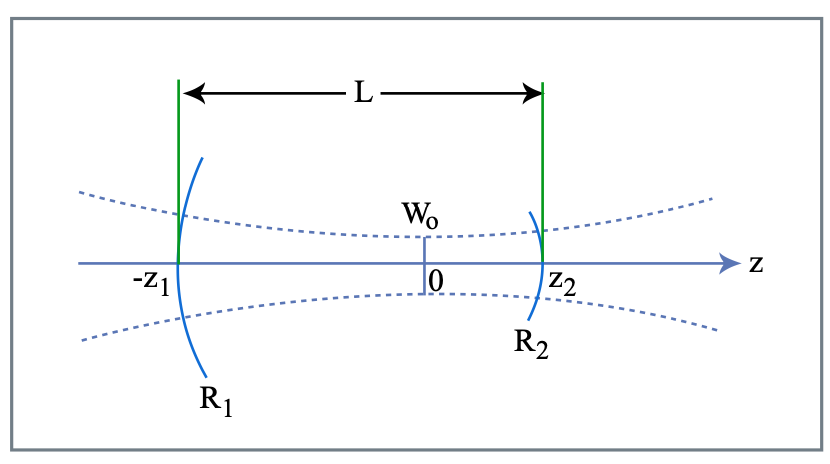
Figura por MIT OCW.
Un cálculo corto da como resultado
\[z_1 = L \dfrac{g_2(g_1 - 1)}{2g_1 g_2 - g_1 - g_2} \nonumber \]
\[= \dfrac{L(L - R_2)}{2L - R_1 - R_2}, \nonumber \]
y, de nuevo, por simetría
\[z_2 = L \dfrac{g_1(g_2 - 1)}{2g_1 g_2 - g_1 - g_2} \nonumber \]
\[= \dfrac{L(L - R_1)}{2L - R_1 - R_2} = L - z_1, \nonumber \]
El tamaño de la mancha en el foco intracavitario es
\[w_0^4 = \left (\dfrac{\lambda L}{\pi} \right )^2 \dfrac{g_1 g_2 (1 - g_1 g_2)}{(2g_1g_2 - g_1 - g_2)^2} \nonumber \]
\[= \left (\dfrac{\lambda }{\pi} \right )^2 \dfrac{L(R_1 - L)(R_2 - L)(R_1 + R_2 - L)}{(R_1 + R_2 - 2L)^2}.\label{eq7.1.37} \]
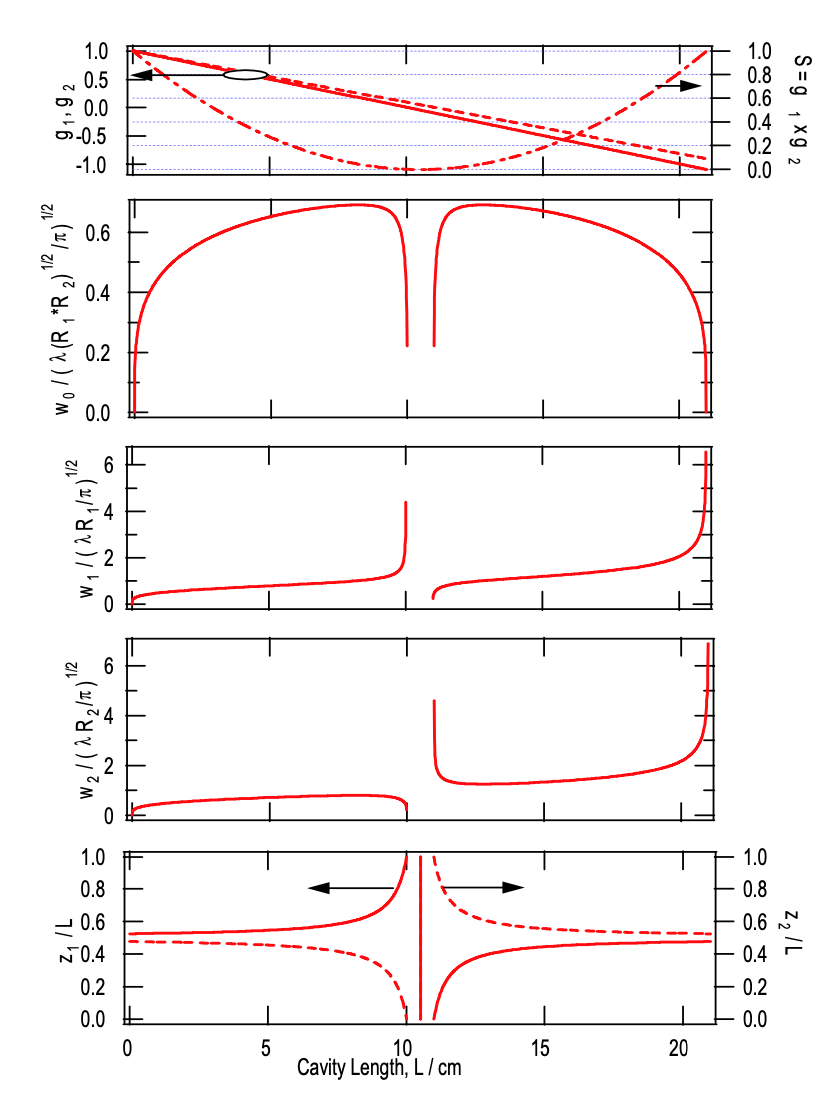
Todas estas cantidades para el resonador de dos espejos se muestran en la Figura 7.11. Obsérvese que todos los resonadores y el haz gaussiano están relacionados con el resonador confocal como se muestra en la Figura 7.10.
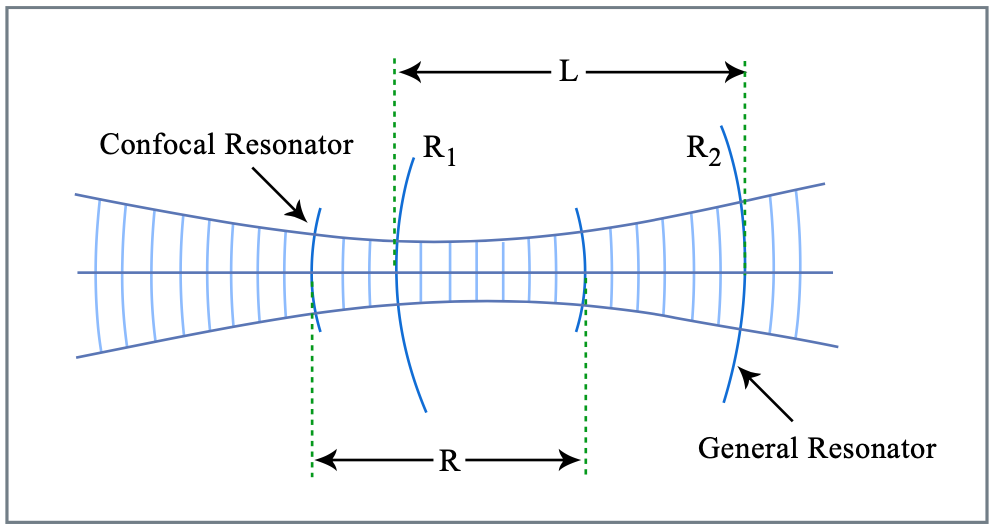
Figura por MIT OCW.
Resonadores de cuatro espejos
Resonadores más complejos, como el resonador de cuatro espejos representado en la Figura 7.12 a) pueden transformarse en un resonador equivalente de dos espejos como se muestra en la Figura 7.4 b) y c)
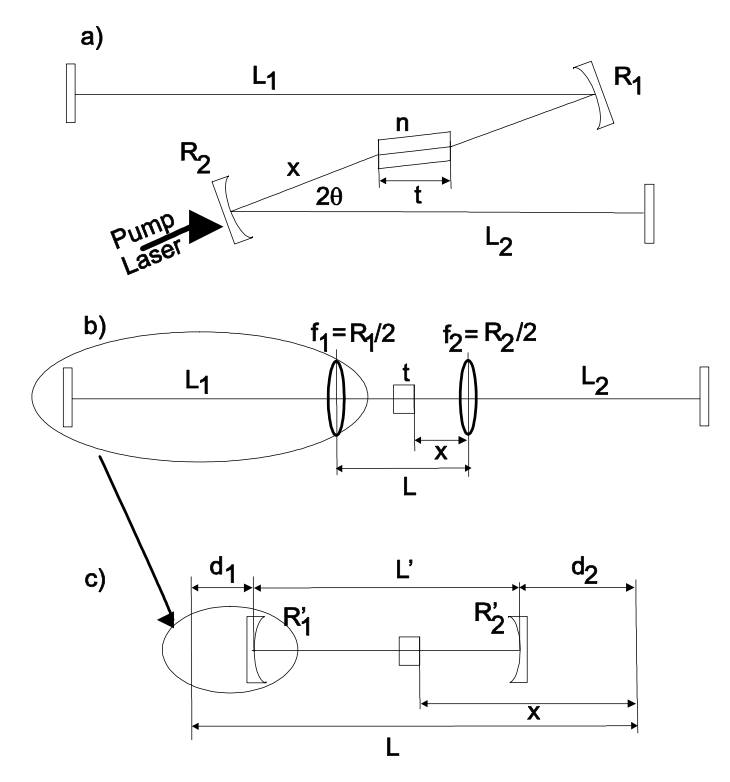
Cada uno de los brazos resonadores (espejo final\(L_1\),,\(R_1\)) o (espejo final\(L_2\),,\(R_2\)) es equivalente a un nuevo espejo con un nuevo radio de curvatura\(R_{1/2}'\) colocado a una\(d_{1/2}\) distancia del plano de referencia anterior [12]. Esto se deduce simplemente del hecho de que cada sistema óptico simétrico es equivalente a una lente colocada a una\(d\) distancia del plano de referencia antiguo
\[\begin{array} {rcl} {M} & = & {\left ( \begin{matrix} A & B \\ C & A \end{matrix} \right ) = \left ( \begin{matrix} 1 & d \\ 0 & 1 \end{matrix} \right ) \left ( \begin{matrix} 1 & 0 \\ \tfrac{-1}{f} & 1 \end{matrix} \right ) \left ( \begin{matrix} 1 & d \\ 0 & 1 \end{matrix} \right )} \\ {} & = & {\left ( \begin{matrix} 1 - \tfrac{d}{f} & d(2 - \tfrac{d}{f}) \\ \tfrac{-1}{f} & 1 - \tfrac{d}{f} \end{matrix} \right )}\end{array} \nonumber \]
con
\[\begin{array} {rcl} {d} & = & {\dfrac{A - 1}{C}} \\ {\dfrac{-1}{f}} & = & {C} \end{array} \nonumber \]
La matriz del brazo resonador 1 viene dada por
\[M = \left ( \begin{matrix} 1 & 0 \\ \tfrac{-2}{R_1} & 1 \end{matrix} \right ) \left ( \begin{matrix} 1 & 2L_1 \\ 0 & 1 \end{matrix} \right ) \left ( \begin{matrix} 1 & 0 \\ \tfrac{-2}{R_1} & 1 \end{matrix} \right ) = \left ( \begin{matrix} 1 - \tfrac{4L_1}{R_1} & 2L_1 \\ \tfrac{-4}{R_1} (1-\tfrac{2L_1}{R_1}) & 1-\tfrac{4L_1}{R_1} \end{matrix} \right ) \nonumber \]
de la que obtenemos
\[d_1 = -\dfrac{R_1}{2} \dfrac{1}{1 - R_1/(2L_1)}, \nonumber \]
\[R_1' = - \left ( \dfrac{R_1}{2} \right )^2 \dfrac{1}{L_1 [1 - R_1/(2L_1)]}. \nonumber \]
Para longitudes de brazo\(L_{1/2}\) mucho mayores que el radio de curvatura, el nuevo radio de curvatura es aproximadamente por un factor de\(\tfrac{R_1}{4L_1}\) menor tamaño. Los valores típicos son\(R_1 = 10\)\(L_1 = 50\) cm y cm. Entonces el nuevo radio de curvatura es\(R_1' = 5\) mm. Las ecuaciones análogas se aplican al otro brazo resonador
\[d_2 = -\dfrac{R_2}{2} \dfrac{1}{1 - R_2/(2L_2)}, \nonumber \]
\[R_2' = -\left ( \dfrac{R_2}{2} \right )^2 \dfrac{1}{L_2 [1 - R_2/(2L_2)]}. \nonumber \]
Tenga en cuenta que los nuevos radios del espejo son negativos para\(R_i/L_i < 1\). La nueva distancia\(L'\) entre los espejos equivalentes es entonces también negativa sobre la región donde el resonador es estable, ver Fig.7.8. Obtenemos
\[L'= L + d_1 + d_2 = L - \dfrac{R_1 + R_2}{2} - \delta \nonumber \]
\[\delta = \dfrac{R_1}{2} \left [\dfrac{1}{1 - R_1/(2L_1)} - 1 \right ] + \dfrac{R_2}{2} \left [\dfrac{1}{1 - R_2/(2L_2)} - 1\right ] \nonumber \]
\[=-(R_1' + R_2') \nonumber \]
o
\[L = \dfrac{R_1 + R_2}{2} - (R_1' + R_2') + L' \nonumber \]
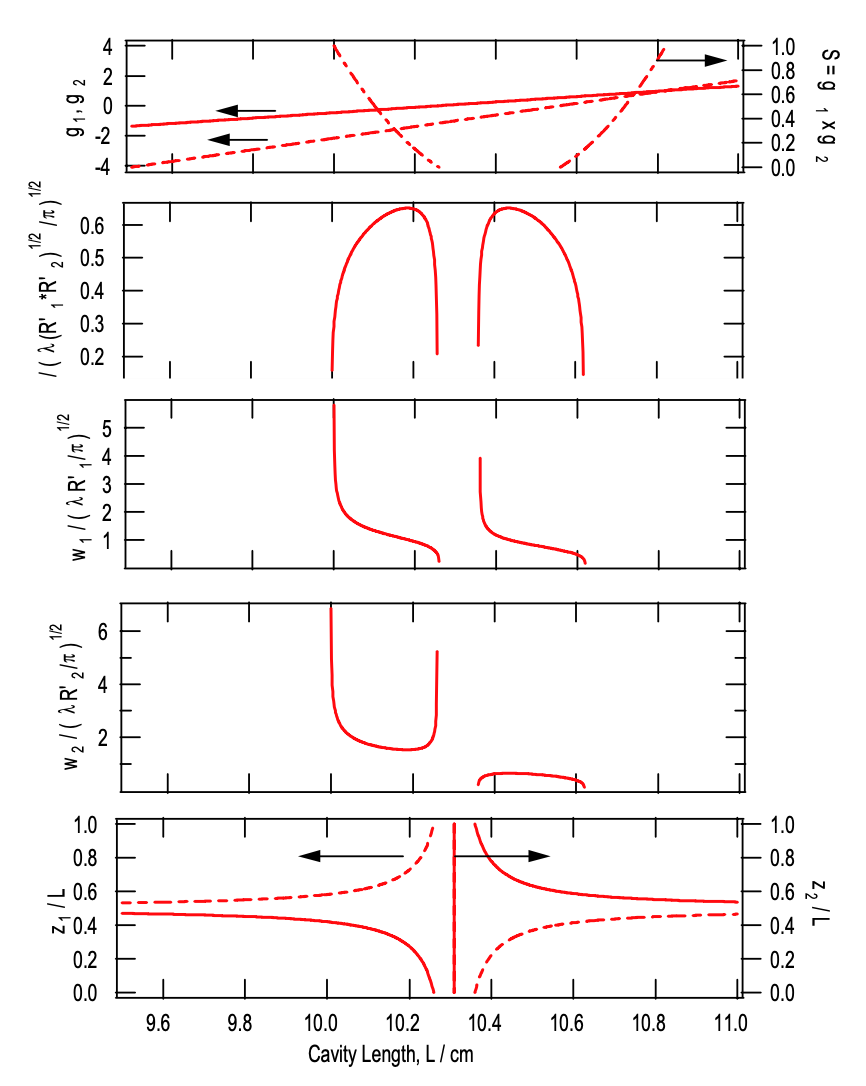
De la discusión en la sección 7.1.2, vemos que los rangos de estabilidad cubren como máximo una distancia\(\delta\). La Figura 7.13 muestra las características del resonador en función de la longitud de la cavidad\(L\) para los siguientes parámetros\(R_1 = R_2 = 10\) cm y\(L_1 =100\) cm y\(L_2 =75\) cm, que conducen a
\[\begin{array} {rcl} {d_1} & = & {-5.26\ cm} \\ {R_1'} & = & {-0.26\ cm}\end{array}\label{eq7.1.49} \]
\[\begin{array} {rcl} {d_2} & = & {-5.36\ cm} \\ {R_2'} & = & {-0.36\ cm}\end{array} \nonumber \]
\[L' = L - 10.62\ cm\label{eq7.1.51} \]
Tenga en cuenta que las fórmulas (\(\ref{eq7.1.27}\)) a (\(\ref{eq7.1.37}\)) se pueden usar con todas las cantidades reemplazadas por las cantidades cebadas correspondientes en la Ec. (\(\ref{eq7.1.49}\)) - (\(\ref{eq7.1.51}\)). El resultado se muestra en la Figura 7.13. La transformación de\(L\) a\(L'\) transforma los rangos de estabilidad de acuerdo con la Figura 7.14. El parámetro confocal del modo láser es aproximadamente igual al rango de estabilidad.
Compensación de astigmatismo
Hasta el momento, hemos considerado los espejos curvos bajo incidencia normal. En una cavidad real este no es el caso y hay que analizar el rendimiento de la cavidad para el haz tangencial y sagital por separado. El medio de ganancia, generalmente una placa delgada con un índice de refracción\(n\) y un espesor\(t\), genera astigmatismo. El astigmatismo significa que los focos de haz para el plano sagital y tangencial no están en la misma posición. Además, las regiones de estabilidad de la cavidad son diferentes para los diferentes planos y el haz de salida es elíptico. Esto es así, porque un haz que entra en una placa bajo un ángulo se refracta de manera diferente en ambos planos, como lo describen diferentes matrices ABCD para el plano tangencial y sagital, ver Tabla 7.1.Afortunadamente, se puede equilibrar el astigmatismo del haz debido a la placa por el astigmatismo introducido por los espejos curvos en un ángulo de incidencia específico\(\theta\) en los espejos [12]. La distancia focal de los espejos curvos bajo un ángulo viene dada por
\[\begin{array} {rcl} {f_s} & = & {f/cos \theta} \\ {f_t} & = & {f \cdot cos \theta} \end{array} \nonumber \]
La distancia de propagación en una placa con espesor t bajo el ángulo de Brewster viene dada por\(t\sqrt{n^2 + 1}/n\). Así, las distancias equivalentes que atraviesan en los planos sagital y tangencial son (Cuadro 7.1),
\[\begin{array} {rcl} {d_s} & = & {t\sqrt{n^2 + 1} /n^2} \\ {d_f} & = & {t \sqrt{n^2 + 1} /n^4} \end{array} \nonumber \]
Las diferentes distancias tienen que compensar las diferentes distancias focales en los planos sagital y tangencial. Asumiendo dos espejos idénticos\(R = R_1 = R_2\), conduce a la condición
\[d_s - 2f_s = d_t - 2f_t. \nonumber \]
Con\(f = R/2\) encontramos
\[R\sin \theta \tan \theta = Nt, \text{where } N = \sqrt{n^2 + 1} \dfrac{n^2 - 1}{n^4} \nonumber \]
Tenga en cuenta que\(t\) es el grosor de la placa en oposición a la longitud de la trayectoria de la viga en la placa. La ecuación da una ecuación cuadrática para\(\cos \theta\)
\[\cos^2 \theta + \dfrac{Nt}{R} \cos \theta - 1 = 0 \nonumber \]
\[\cos \theta_{1/2} = - \dfrac{Nt}{2R} \pm \sqrt{1 + \left (\dfrac{Nt}{2R} \right )^2} \nonumber \]
Dado que el ángulo es positivo, la única solución es
\[\theta = \text{arccos} \left [ \sqrt{1 + \left (\dfrac{Nt}{2R} \right )^2} - \dfrac{Nt}{2R}\right ]. \nonumber \]
Esto concluye el diseño y análisis del resonador lineal.
Efectos de lente Kerr
A altas intensidades, el índice de refracción en el medio de ganancia se vuelve dependiente de la intensidad
\[n = n_0 + n_2I. \nonumber \]
El perfil de intensidad gaussiana del haz crea un perfil de índice dependiente de la intensidad
\[I(r) = \dfrac{2P}{\pi w^2} \exp [-2 (\dfrac{r}{w})^2 ]. \nonumber \]
En el centro de la viga el índice puede ser appoximado por una parábola
\[n(r) = n_0' (1 - \dfrac{1}{2} \gamma^2 r^2 ), \text{where} \nonumber \]
\[n_0' = n_0 + n_2 \dfrac{2P}{\pi w^2}, \gamma = \dfrac{1}{w^2} \sqrt{\dfrac{8n_2P}{n_0'\pi}}. \nonumber \]
Un corte delgado de un medio de índice parabólico equivale a una lente delgada. Si el medio índice parabólico tiene un grosor\(t\), entonces la matriz ABCD que describe la propagación del rayo a través del medio con incidencia normal es [16]
\[M_K = \left (\begin{matrix}\cos \gamma t & \tfrac{1}{n_0' \gamma} \sin \gamma t \\ -n_0' \gamma \sin \gamma t & \cos \gamma t \end{matrix} \right ). \nonumber \]
Tenga en cuenta que, para pequeños\(t\), recuperamos la fórmula de lente delgada (\(t \to 0\), pero\(n_0'\gamma^2 t = 1/f = \text{ const}\).). Si el medio Kerr se coloca bajo el ángulo de Brewster, nuevamente tenemos que diferenciar entre los planos sagital y tangencial. Para el plano sagital, el tamaño del haz que ingresa al medio sigue siendo el mismo, pero para el plano tangencial, se abre por un factor\(n_0'\)
\[\begin{array} {rcl} {w_s} & = & {w} \\ {w_t} & = & {w \cdot n_0'} \end{array} \nonumber \]
El spotsize propocional a\(w^2\) tiene que ser reemplazado por\(w^2 =w_sw_t\) .Por lo tanto, bajo la incidencia del ángulo Brewster, los dos planos comienzan a interactuar durante la propagación a medida que los parámetros gamma se acoplan entre sí por
\[\gamma_s = \dfrac{1}{w_s w_t} \sqrt{\dfrac{8n_2 P}{n_0' \pi}} \nonumber \]
\[\gamma_t = \dfrac{1}{w_s w_t} \sqrt{\dfrac{8n_2 P}{n_0' \pi}} \nonumber \]
Sin pruebas (ver [12]), obtenemos las matrices listadas en el Cuadro 7.2. Para baja
| Elemento óptico | Matriz ABCD |
| Kerr Incidencia Normal Media | \ (M_K =\ izquierda (\ begin {matriz}\ cos\ gamma t &\ tfrac {1} {n_0'\ gamma}\ sin\ gamma t\\ -n_0'\ gamma\ sin\ gamma t &\ cos\ gamma t\ fin {matriz}\ derecha)\ nonumber\] |
| Kerr Plano Sagittal Medio | \ (M_ {k_s} =\ izquierda (\ begin {matriz}\ cos\ gamma_s t &\ tfrac {1} {n_0'\ gamma_s}\ sin\ gamma_s t\\ -n_0'\ gamma_s\ sin\ gamma_s t &\ cos\ gamma_s t\ end {matriz}\ derecha)\ nonumber\] |
| Kerr Plano Tangencial Medio | \ (M_ {k_t} =\ izquierda (\ begin {matriz}\ cos\ gamma_t &\ tfrac {1} {n_0'^3\ gamma_t}\ sin\ gamma_t\\ -n_0'^3\ gamma_t\ sin\ gamma_t &\ cos\ gamma_t\ end {matriz}\ derecha)\ nonumber\] |
Cuadro 7.2: Matrices ABCD para medios Kerr, modeladas con un perfil de índice parabólico\(n(r) = n_0' (1 - \tfrac{1}{2} \gamma^2 r^2)\).
potencia pico\(P\), se puede descuidar el efecto de lente Kerr y las matrices en la Tabla 7.2 convergen hacia las de propagación lineal. Cuando el láser está bloqueado en modo, la potencia máxima\(P\) aumenta en muchos órdenes de magnitud, aproximadamente la relación entre el tiempo de ida y vuelta de la cavidad y el ancho de pulso final, asumiendo una energía de pulso constante. Para un láser de 100 MHz, 10 fs, esto es un factor de\(10^6\). Con la ayuda de la formulación matricial del efecto Kerr, se pueden encontrar iterativamente las cinturas del haz de estado estacionario en el láser. A partir de los valores para la cavidad lineal, se puede obtener un nuevo modo de resonador, que proporciona valores mejorados para las cinturas del haz calculando una nueva matriz de propagación de ida y vuelta de cavidad basada en una potencia máxima dada\(P\). Este esquema se puede iterar hasta que solo haya un cambio insignificante de iteración a iteración. Usando tal simulación, se puede encontrar el cambio en la cintura del haz en una cierta posición en el resonador entre la operación cw y la operación de modo bloqueado, que se puede expresar en términos del parámetro delta
\[\delta_{s, t} = \dfrac{1}{p} \dfrac{w_{s, t} (P, z) - w_{s, t} (P = 0, z)}{w_{s, t} (P = 0, z)} \nonumber \]
donde\(p\) es la relación entre la potencia pico y la potencia crítica para el autoenfoque
\[p = P/P_{crit}, \text{ with } P_{crit} = \lambda_L^2/(2\pi n_2 n_0^2). \nonumber \]
Para conocer la sensibilidad de una determinada configuración de cavidad para KLM, es interesante calcular las variaciones\(\delta_{s,t}\) normalizadas del tamaño del haz en función de los parámetros más críticos de la cavidad. Para la cavidad de cuatro espejos, los parámetros naturales a elegir son la distancia entre el cristal y la posición del espejo de bombeo\(x\), y la distancia del espejo\(L\), ver Figura 7.12. La Figura 7.15 muestra dicha gráfica para los siguientes parámetros de cavidad\(R_1 = R_2 = 10\)\(L_1 = 104\) cm,\(L_2 = 86\) cm, cm,\(t = 2\) mm\(n = 1.76\) y\(P = 200\) kW.
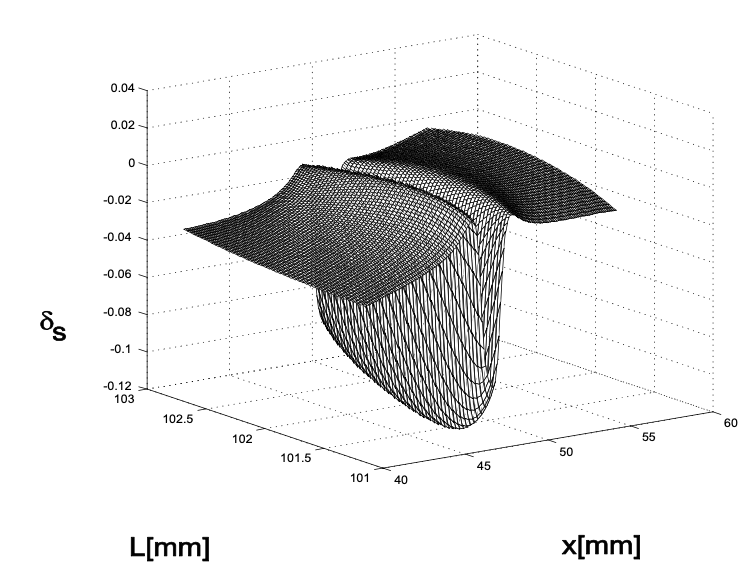
El efecto de lente Kerr se puede explotar de diferentes maneras para lograr el bloqueo de modo.
KLM de apertura suave
En el caso del KLM de apertura suave, la cavidad se ajusta de tal manera que el efecto de lente Kerr conduce a una contracción del modo láser cuando se bloquea el modo. La ganancia no saturada en un láser depende de la superposición del modo de bomba y el modo láser. A partir de las ecuaciones de velocidad para la distribución radial de fotones\(N(r)\) y la inversión\(N_P (r)\) de un láser, que son proporcionales a las intensidades del haz de bombeo y del rayo láser, obtenemos una ganancia, que es proporcional al producto de\(N(r)\) y\(N_P(r)\). Si asumimos que el foco del modo láser y el modo de bombeo están en la misma posición y descuidamos la variación de ambos haces en función de la distancia, obtenemos
\[\begin{array} {rcl} {g} & \sim & {N(r)*N_p(r) r dr} \\ {} & \sim & {\int_{0}^{\infty} \dfrac{2P_P}{\pi w_P^2} \exp \left [-\dfrac{2r^2}{w_P^2} \right ] \dfrac{2}{\pi w_L^2} \exp \left [-\dfrac{2r^2}{w_L^2} \right ] r dr} \end{array}\nonumber \]
Con las secciones transversales del haz de la bomba y el rayo láser en el medio de ganancia\(A_L = \pi w_L^2\),\(A_P = \pi w_P^2\) y, obtenemos
\[g \sim \dfrac{1}{A_p + A_L} \nonumber. \nonumber \]
Si el haz de bombeo es mucho más fuerte enfocado en el medio de ganancia que el rayo láser, una contracción de la sección transversal del modo láser en el medio de ganancia conduce a una ganancia aumentada. Cuando el láser opera en estado estacionario, el cambio en la ganancia saturada tendría que ser utilizado para la investigación. No obstante, el argumento general se lleva a cabo incluso para este caso. La Figura 7.16 muestra la variación del tamaño del modo láser en y cerca del cristal en un láser KLM de apertura suave debido al autoenfoque.
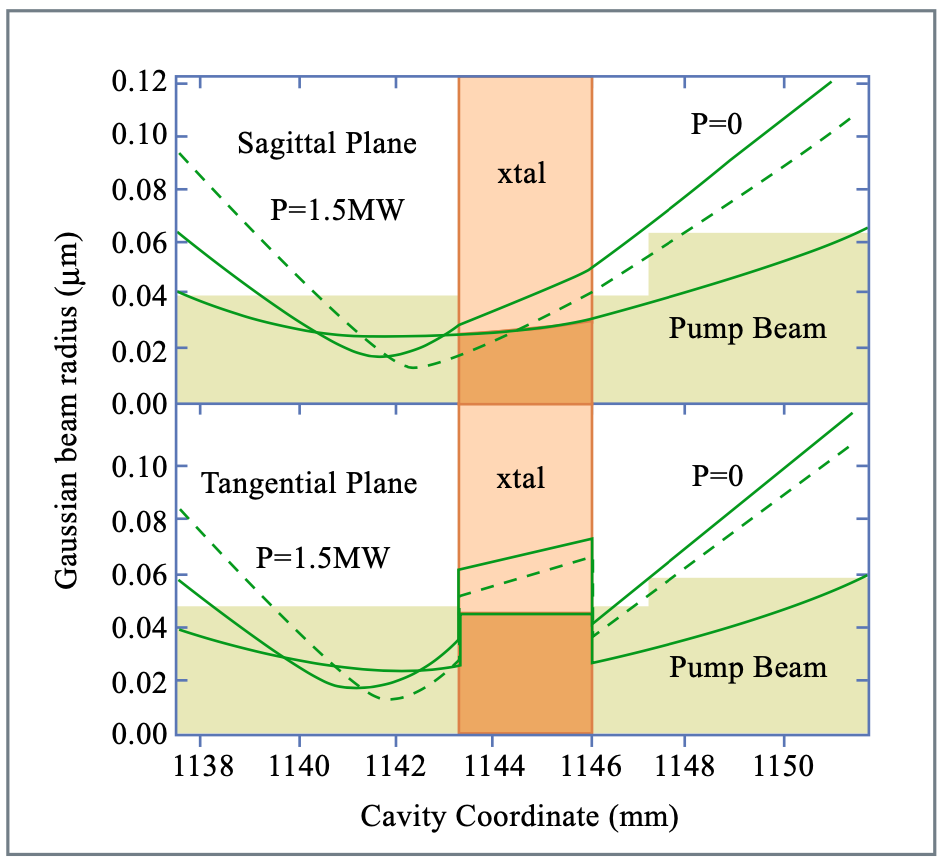
Figura por MIT OCW.
KLM de apertura dura
En un KLM-Laser de apertura dura, uno de los brazos del resonador contiene (generalmente cerca de los espejos finales) una abertura tal que corta ligeramente el haz. Cuando se produce una lente Kerr y conduce a una contracción de la viga en esta posición, las pérdidas de la viga se reducen. Obsérvese que dependiendo de si la abertura está posicionada en el brazo largo o corto del resonador, el punto operativo de la cavidad en la que la lente Kerr favorece u se opone al bloqueo de modo puede ser bastante diferente (ver Figura 7.13).