7.2: Bloqueo de Modo de Pulso Aditivo

Al igual que el bloqueo de modo Kerr-Lens también Bloqueo de Modo de Pulso Aditivo (APM) es un efecto absorbente saturable artificial [17] [18] [19] [20] [21] [22]. La figura 7.17 muestra el principio general en funcionamiento. Una pequeña fracción de la luz emitida desde la cavidad principal del láser se inyecta externamente en una fibra no lineal. En la fibra se produce un SPM fuerte e introduce un desplazamiento de fase significativo entre el pico y las alas del pulso. En el caso mostrado el desplazamiento de fase es\(\pi\).

Una parte del pulso modificado y fuertemente distorsionado se reinyecta en la cavidad de una manera interferométricamente estable, de tal manera que el pulso inyectado interfiere constructivamente con el siguiente pulso de cavidad en el centro y destructivamente en las alas. Esta superposición conduce a un pulso intracavitario más corto y la conformación del pulso generada por este proceso es idéntica a la obtenida de un absorbedor saturable rápido. Nuevamente, se genera una acción absorbente saturable artificial.

Figura 7.18: Esquema del interferómetro Mach-Zehnder no lineal.

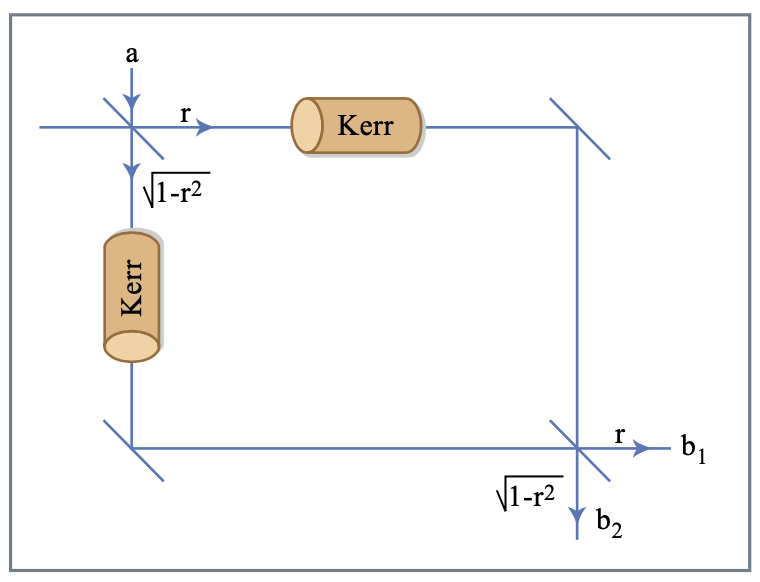
Figura por MIT OCW.

La Figura 7.18 muestra un interferómetro simple no lineal. En la práctica, dicho interferómetro puede realizarse de manera autoestabilizada mediante el uso de ambas polarizaciones en un medio Kerr isotrópico con polarizador y analizador como se muestra en la Figura 7.19.

Figura 7.19: Interferómetro Mach-Zehnder no lineal utilizando rotación polar no lineal en una fibra [25].

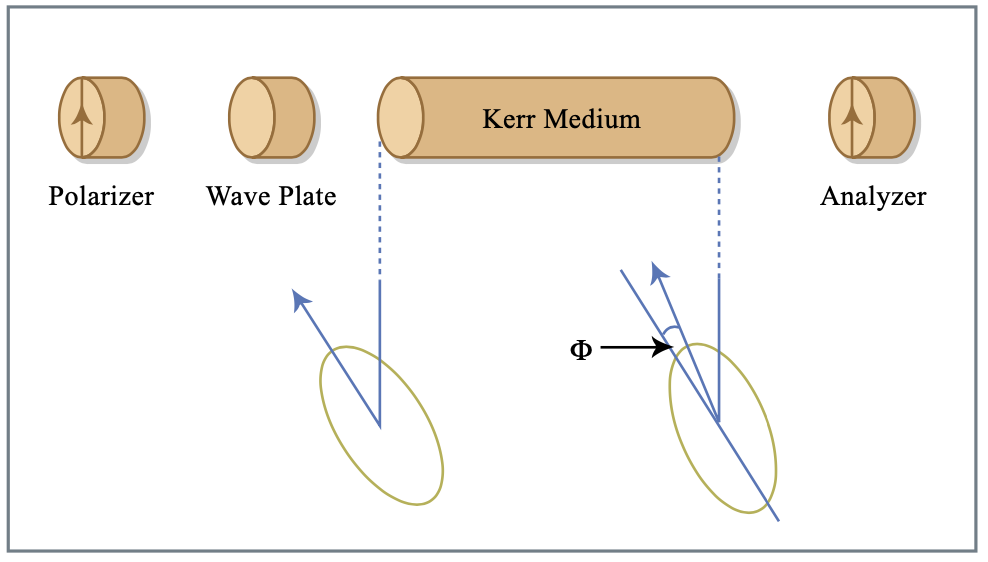
Figura por MIT OCW.

El efecto Kerr gira la elipse de polarización y, por lo tanto, transforma la modulación de fase en modulación de amplitud. La operación se realiza en correspondencia uno a uno con la del interferómetro no lineal Mach-Zehnder de la Fig. 7.18. El sistema de la Figura 7.18 puede analizarse de manera bastante simple y por lo tanto merece la pena mirar la derivación y los supuestos implícitos. Los acopladores son descritos por las matrices de dispersión

\[S = \begin{bmatrix} r & \sqrt{1 - r^2} \\ \sqrt{1 - r^2} & - r \end{bmatrix}. \nonumber \]

Las salidas del interferómetro son entonces

\[b_1 = [r^2 e^{-j \phi_1} + (1 - r^2) e^{-j \phi_2} ] a, \nonumber \]

\[b_2 = 2r \sqrt{1 - r^2} \exp \left [ - j \dfrac{\phi_1 + \phi_2}{2} \right ] \sin \left [ \dfrac{\phi_2 - \phi_1}{2} \right ] a, \nonumber \]

\(\phi_1\)y\(\phi_2\) son los desplazamientos de fase en los dos brazos compuestos tanto por contribuciones lineales de “sesgo” como por\(\phi_{bi}\) los desplazamientos de fase de Kerr\(\phi_{Ki}\)

\[\phi_i = \phi_{bi} + \phi_{Ki}, (i = 1, 2), \nonumber \]

\[\phi_{Ki} = \kappa_i |a|^2, (i = 1,2). \nonumber \]

La potencia en el puerto de salida dos está relacionada con las pérdidas lineales y no lineales

\[\begin{array} {rcl} {|b_2|^2} & = & {2r^2 (1 - r^2) (1 - \cos [\phi_2 - \phi_1])|a|^2} \\ {} & = & {2r^2 ( 1 - r^2) \{(1 - \cos [\phi_{b2} - \phi_{b1}]) + \sin [\phi_{b2} - \phi_{b1}] (\phi_{K2} - \phi_{K1}) \} |a|^2} \end{array} \nonumber \]

Dependiendo de la fase de polarización\(\phi_b = \phi_{b2} - \phi_{b1}\), la pérdida de amplitud es

\[l = r^2 (1 - r^2) (1 - \cos \phi_b) |a|^2,\label{eq7.2.7} \]

y el\(\gamma\) parámetro −del absorbedor saturable rápido equivalente es

\[\gamma = (\kappa_1 - \kappa_2)r^2 (1 - r^2) \sin \phi_b.\label{eq7.2.8} \]

Si el interferómetro forma parte de un sistema resonante, la frecuencia del sistema se ve afectada por el desplazamiento de fase del interferómetro y a su vez afecta la fase.

Cuando las frecuencias resonantes del sistema lineal (\(\gamma = \delta = 0\)) sin el interferómetro deben permanecer las frecuencias resonantes con el interferómetro, el desplazamiento de fase neto del interferómetro tiene que elegirse para que sea cero. Dado que se ha asumido una pequeña pérdida y por lo tanto\(r^2 \gg 1 - r^2\)

\[\text{Im } [r^2 e^{-j \phi_{b1}} + (1 - r^2) e^{-j \phi_{b2}}] = \text{Im } [r^2 (1 - j \phi_{b1}) + (1 - r^2) e^{-j \phi_{b2}}] = 0 \nonumber \]

o

\[\phi_{b1} = \dfrac{-(1 - r^2)}{r^2} \sin \phi_{b2}. \nonumber \]

y\(\cos \phi_{b1} = 1\). Con este ajuste, la respuesta del interferómetro se convierte

\[\begin{array} {rcl} {b_1} & \approx & {a + \Delta a = a - (1 - r^2)(1 - \cos \phi) a} \\ {} & \ & {-(1 - r^2)(\phi_{K2} - \phi_{K1}) \sin \phi a} \\ {} & \ & {-j r^2 \phi_{K1} - j (1 - r^2) \phi_{K2} \cos \phi a,} \end{array} \nonumber \]

donde hemos establecido\(\phi = \phi_{b2}\). Esto da para los parámetros de la ecuación maestra\(l, \gamma\) y\(\delta\)

\[l = (1 - r^2) (1 - \cos \phi), \nonumber \]

\[\gamma = (\kappa_1 - \kappa_2)(1 - r^2) \sin \phi, \nonumber \]

\[\delta = \kappa_1 r^2 + \kappa_2 (1 - r^2) \cos \phi. \nonumber \]

Debido a la elección especial de la fase de polarización no hay contribución del interferómetro no lineal a la fase lineal. Esto concuerda con las expresiones (\(\ref{eq7.2.7}\)) y (\(\ref{eq7.2.8}\)). Los coeficientes de Kerr son

\[\kappa_1 = r^2 \left (\dfrac{2\pi}{\lambda} \right ) \dfrac{n_2}{A_{eff}} L_{kerr}, \nonumber \]

\[\kappa_2 = (1 - r^2) \left (\dfrac{2\pi}{\lambda} \right ) \dfrac{n_2}{A_{eff}} L_{kerr}. \nonumber \]

Aquí,\(\lambda\) es la longitud de onda del espacio libre del campo óptico,\(A_{eff}\) es el área efectiva del modo,\(n_2\) el índice de refracción dependiente de la intensidad, y\(L_{Kerr}\) es la longitud del medio Kerr. La Figura 7.20 es el coeficiente de absorbedor saturable\(\gamma\) normalizado al efecto de pérdida y Kerr (nótese que\(\gamma\) va a cero cuando la pérdida va a cero) en función de\(r^2\)

Figura 7.20: Coeficiente\(\gamma /[(\tfrac{2\pi}{\lambda}) \tfrac{n_2}{A_{eff}} L_{Kerr} l]\) normalizado del absorbedor saturable en función de\(r^2\) con la pérdida\(l\) como parámetro [25].

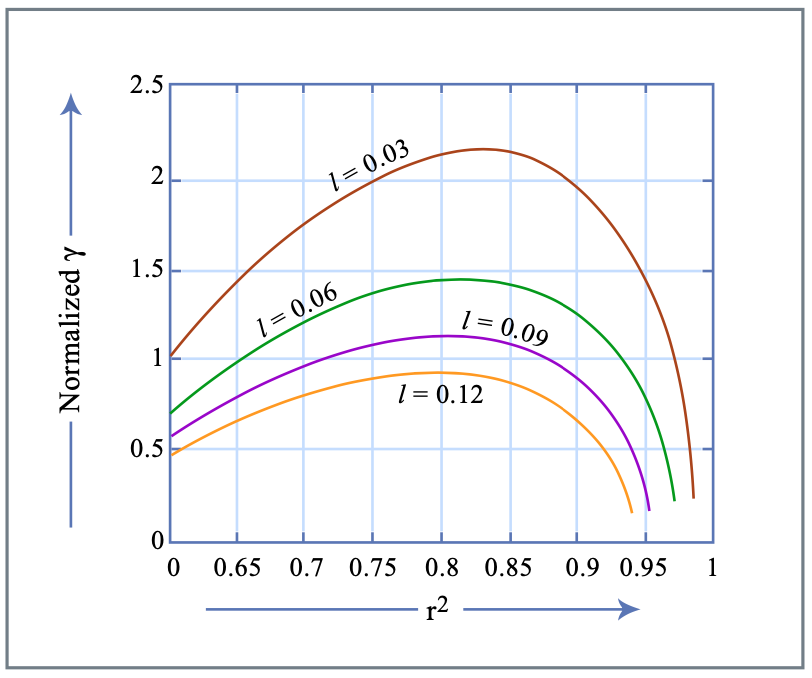
Figura por MIT OCW.

Se pueden lograr grandes coeficientes de absorción saturables a valores de pérdida moderada.

Bibliografía

[1] D. E. Spence, P. N. Kean, W. Sibbett,” Generación de pulsos de 60 fseg a partir de un láser Ti:Sapphire autobloqueado en modo”, Opt. Lett. 16, pp. 42 — 44 (1991)

[2] U. Keller, G. W 'Thooft, W. H. Knox, J. E. Cunningham,” Pulsos femtosec- ond de un láser Ti:Zafiro bloqueado de modo pasivo de arranque automático continuo,” Opt. Lyt. 16, pp.1022 — 1024 (1991).

[3] D. K. Negus, L. Spinelli, N. Goldblatt, G. Feugnet,” Sub-100 femtosec- ond generación de pulsos por lente Kerr modelocking en Ti:Sapphire,” en Ad- vanced Solid-State Lasers, G. Dube, L. Chase, Eds. (Optical Society of America, Washington, D.C., 1991), 10, pp.120 — 124.

[4] F. Salin, J. Squier y M. Piche,” Bloqueo de modo de láseres Ti:Al2O3 y autoenfoque: una aproximación gaussiana,” Opt. Lyt. 16, pp. 1674 — 1676 (1991).

[5] M. Piche, F. Salin,” Bloqueo de modo automático de láseres de estado sólido sin aper- turas”, Opt. Lyt. 18, pp. 1041 — 1043 (1993).

[6] G. Cerullo, S. De Silvestri, V. Magni, L. Pallaro,” Resonadores para Kerr- modo de lente bloqueado femtosegundo Ti:láseres de zafiro”, Opt. Lyt. 19, pp. 807 — 809 (1994).

[7] G. Cerullo, S. De Silvestri, V. Magni,” Modo de lente Kerr de arranque automático- Bloqueo de un Láser Ti:Zafiro”, Opt. Lyt. 19, pp. 1040 — 1042 (1994).

[8] L. Dahlström,” Modelocking pasivo y Q-switching de láseres de alta potencia mediante el efecto óptico Kerr”, Opt. Comm. 5, pp. 157 — 162 (1972).

[9] E. G. Lariontsev y V. N. Serkin,” Posibilidad de utilizar el autoenfoque para aumentar el contraste y el estrechamiento de los pulsos de luz ultracortos”, Sov. J. Quant. Electron. 5, pp. 769 — 800 (1975).

[10] K. Sala, M. C. Richardson, N. R. Isenor,” Modelocking pasivo de Láseres con el modulador óptico de efectos Kerr”, IEEE J. Quant. Electrón. QE- 13, pp. 915 — 924 (1977).

[11] H. Kogelnik y T. Li,” Rayos Láser y Resonadores”, Appl. Opt. 5, pp. 1550 — 1566 (1966).

[12] H. Kogelnik, E. P. Ippen, A. Dienes y C. V. Shank,” Cavidades compensadas astigmáticamente para láseres de tinte CW”, IEEE J. Quantum Electron. QE-8, pp. 373 — 379 (1972).

[13] O. Svelto,” Principles of Lasers”, 3a edición, Plenum Press, Nueva York y Londres, (1989).

[14] H. A. Haus,” Campos y Olas en Optoelectrónica”, Prentice Hall 1984.

[15] F. K. Kneubühl y M. W. Sigrist,” Laser”, 3a Edición, Teubner Ver- lag, Stuttgart (1991).

[16] A. E. Siegman,” Láseres”, Libros de Ciencias Universitarias, Mill Valley, Califor- nia (1986).

[17] K. J. Blow y D. Wood,” Láseres modelocados con cavidades externas no lineales”, J. Opt. Soc. Am. B 5, pp. 629 — 632 (1988).

[18] K. J. Blow y B. P. Nelson,” Bloqueo de modo mejorado de un láser de centro F con una cavidad externa no lineal no solitón”, Opt. Lyt. 13, pp. 1026 —1028 (1988).

[19] P. N. Kean, X. Zhu, D. W. Crust, R. S. Grant, N. Langford y W. Sibbett,” Bloqueo de modo mejorado de láseres color-centro,” Opt. Lett. 14, pp. 39 — 41 (1989).

[20] J.Mark, L.Y.Liu, K.L.Hall, H.A.hausande.P.IPPEN,” Generación de pulsos de femtosegundos en un láser con un resonador externo no lineal”, Opt. Lett. 14, pp. 48 — 50 (1989).

[21] E. P. Ippen, H. A. Haus y L. Y. Liu,” Bloqueo de modo pulso aditivo”, J. Opt. Soc. Am. B 6, pp. 1736 — 1745 (1989).

[22] J. Goodberlet, J. Jacobson y J. G. Fujimoto, P. A. Schultz y T. Y. Fan,” Láser Nd:YAG bombeado por diodo bloqueado en modo de pulso aditivo-autoarrancador”, Opt. Lyt. 15, pp. 504-506 (1990).

[23] F. X. Kärtner, L. R. Brovelli, D. Kopf, M. Kamp, I. Calasso y U. Keller:” Control de la Dinámica Láser de Estado Sólido por Semiconductores De- vicios, Ingeniería Óptica, 34, pp. 2024 — 2036, (1995).

[24] K. Tamura,” Aditivo-pulso limitante”, Opt. Lett. 19, pp. 31 — 33 (1994).

[25] H. A. Haus, J. G. Fujimoto y E. P. Ippen,” Teoría Analítica del Pulso Addi- tivo y Bloqueo del Modo de Lente Kerr”, IEEE J. Quantum Electron. 28, pp. 2086 — 2095 (1992).

[26] H. A. Haus, J. G. Fujimoto y E. P. Ippen,” Estructuras de Bloqueo de Modo Pulso Aditivo”, J. Opt. Soc. Am. 8, pp. 2068 — 2076 (1991).