10.3: Compuerta óptica de frecuencia resuelta (FROG)
- Page ID
- 84983
Seguimos de cerca el bock del inventor de la RANA Rich Trebino. En la activación óptica resuelta en frecuencia, el pulso a caracterizar es cerrado por otro pulso ultracorto [5]. La activación no es una técnica simple de muestreo lineal, pero los pulsos se cruzan en un medio con una no linealidad instantánea (\(\chi (2)\)o\(\chi (3)\)) de la misma manera que en una medición de autocorrelación (Figuras 10.1 y 10.10). La rana-señal es una convolución del campo eléctrico desconocido\(E(t)\) con el campo gating-field\(g(t)\) (a menudo una copia del pulso desconocido en sí). Sin embargo, después de la interacción del pulso a medir y el pulso de puerta, la radiación óptica no lineal emitida no se pone en un simple fotodetector, sino que se detecta espectralmente resuelta. La forma general de la intensidad resuelta en frecuencia, o Espectrograma\(S_F (\tau, \omega)\) viene dada por
\[S_F (\tau, \omega) \propto \left|\int_{-\infty}^{\infty} E(t) \cdot g(t - \tau) e^{-j \omega t} dt \right|^2\label{eq10.3.1} \]
Imagen eliminada por consideraciones de derechos de autor.
Figura 10.10: El espectrograma de una forma de onda E (t) indica la intensidad y frecuencia en un intervalo de tiempo dado [5].
Las representaciones de señales, o formas de onda en general, por distribuciones de tiempo-frecuencia tienen una larga historia. Lo más notable es que las partituras musicales son una secuencia temporal de tonos que dan su frecuencia y volumen, ver Figura 10.11.

Las representaciones de tiempo-frecuencia son bien conocidas en la comunidad de radares, procesamiento de señales y mecánica cuántica [9] (Espectrograma, Wigner-Distribución, Husimi-Distribución,...), La Figura 10.12 muestra el espectrograma de pulsos gorjeados de manera diferente. Al igual que una partitura musical, el espectrograma muestra visualmente la frecuencia vs. tiempo.
Imagen eliminada por consideraciones de derechos de autor.
Figura 10.12: Al igual que una partitura musical, el espectrograma muestra visualmente la frecuencia vs. tiempo [5].
Tenga en cuenta que el pulso de puerta en la técnica de medición FROG no debe ser muy corto. De hecho si tenemos
\[g(t) \equiv \delta (t) \nonumber \]
entonces
\[S_F (\tau, \omega) = |E(\tau)|^2 \nonumber \]
y la información de la fase se pierde por completo. No hay necesidad de pulsos de puerta cortos. Una longitud de puerta del orden de la longitud del pulso es suficiente. Resuelve temporalmente los componentes lentos y espectralmente los componentes rápidos.
Polarización Puerta FROG
La Figura 10.13 muestra la configuración [6] [7]. FROG se basa en la generación de un pulso de puerta bien definido, eventualmente aún no conocido. Esto se puede lograr utilizando el pulso a medir y una interacción no lineal ultrarrápida. Por ejemplo, el efecto Kerr electrónico se puede utilizar para inducir una modulación de polarización ultrarrápida, que puede computar el pulso con una copia del mismo pulso.
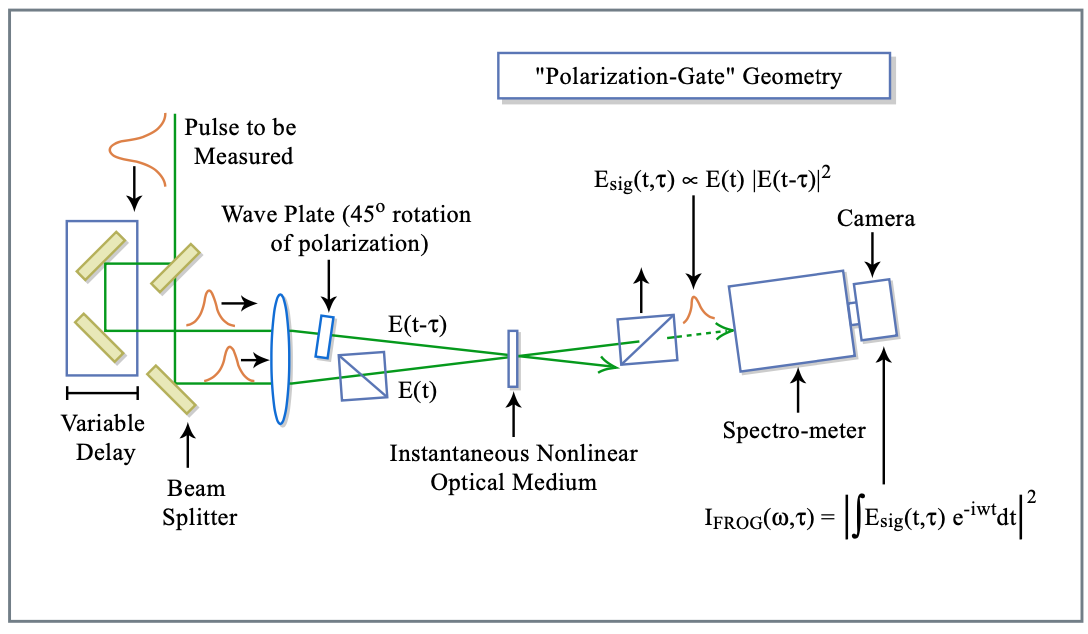
La señal analizada en la traza de FROG es, ver Figura 10.14,
\[E_{sig} (t, \tau) = E(t) |E(t - \tau)|^2\label{eq10.3.4} \]
Imagen eliminada por consideraciones de derechos de autor.
Figura 10.14: El pulso de señal refleja el color del pulso cerrado en ese momento\(2\tau/3\) [5]
Las trazas FROG generadas a partir de un PG-FROG para pulsos chirped son idénticas a la Figura 10.12. La Figura 10.15 muestra trazas FROG de pulsos más complicados
Imagen eliminada por consideraciones de derechos de autor.
Figura 10.15: Rastros de RANA de pulsos más complicados.
Algoritmo de inversión de
Los algoritmos de inversión de espectrogramas necesitan conocer la función de puerta\(g(t - \tau)\), que en el caso dado está relacionada con el pulso aún desconocido. Entonces, ¿cómo se llega de la traza de la FANA a la forma del pulso con respecto a la amplitud y fase? Si existe tal algoritmo, que produce soluciones, surge la cuestión de la singularidad de esta solución. Para obtener una idea de estos temas, nos damos cuenta, que el rastro de la FROG se puede escribir como
\[I_{FROG} (\tau, \omega) \propto \left|\int_{-\infty}^{\infty} E_{sig} (t, \tau) e^{-j \omega t} dt \right|^2 \nonumber \]
Escribir el campo de señal como una transformada de Fourier en la variable de tiempo, i.e.
\[E_{sig} (t, \tau) = \int_{-\infty}^{\infty} \hat{E}_{sig} (t, \Omega) e^{-j \Omega \tau} d \Omega \nonumber \]
rendimientos
\[I_{FROG} (\tau, \omega) \propto \left|\int_{-\infty}^{\infty} \hat{E}_{sig} (t, \Omega) e^{-j \omega t - j \Omega \tau} dt d\Omega \right|^2.\label{eq10.3.7} \]
Esta ecuación muestra que el rastro de rana es el cuadrado de magnitud de una transformada bidimensional de Fourier relacionada con el campo de señal\(E_{sig}(t,\tau)\). La inversión de la Ec. (\(\ref{eq10.3.7}\)) se conoce como el problema de recuperación de la fase 2D. Afortunadamente existen algoritmos para esta inversión [8] y se sabe que la magnitud (o magnitud cuadrada) de una transformada 2D-Fourier (FT) determina esencialmente de manera única también su fase, si se dan condiciones adicionales, como el soporte finito o la relación (\(\ref{eq10.3.4}\)). Esencialmente único significa, que hay ambigüedades pero no son densas en el espacio de función de posibles transformaciones 2D, es decir, tienen probabilidad cero de ocurrir.
Además, el pulso desconocido se\(E(t)\) puede obtener fácilmente del campo de señal modificado\(\hat{E}_{sig} (t,\Omega)\) porque
\ [\ begin {alinear*}\ hat {E} _ {sig} (t,\ Omega) &=\ int_ {-\ infty} ^ {\ infty} E_ {sig} (t,\ tau) e^ {j\ Omega\ tau} d
\ tau\ [4pt] &=\ int_ {-\ infty} ^ {\ infty} E (t) g (t -\ tau) e^ {-j\ Omega\ tau} d\ tau
\\[4pt] &= E(t) G^* (\Omega) e^{-j\Omega t} \end{align*} \nonumber \]
con
\[G(\Omega) = \int_{-\infty}^{\infty} g(\tau) e^{-\Omega \tau} d\tau. \nonumber \]
Así hay
\[E(t) \propto \hat{E}_{sig} (t, 0). \nonumber \]
La única condición es que la función de puerta se elija de tal manera que\(G(\Omega) \ne 0\). Esto es muy poderoso.
Algoritmo de Transformada
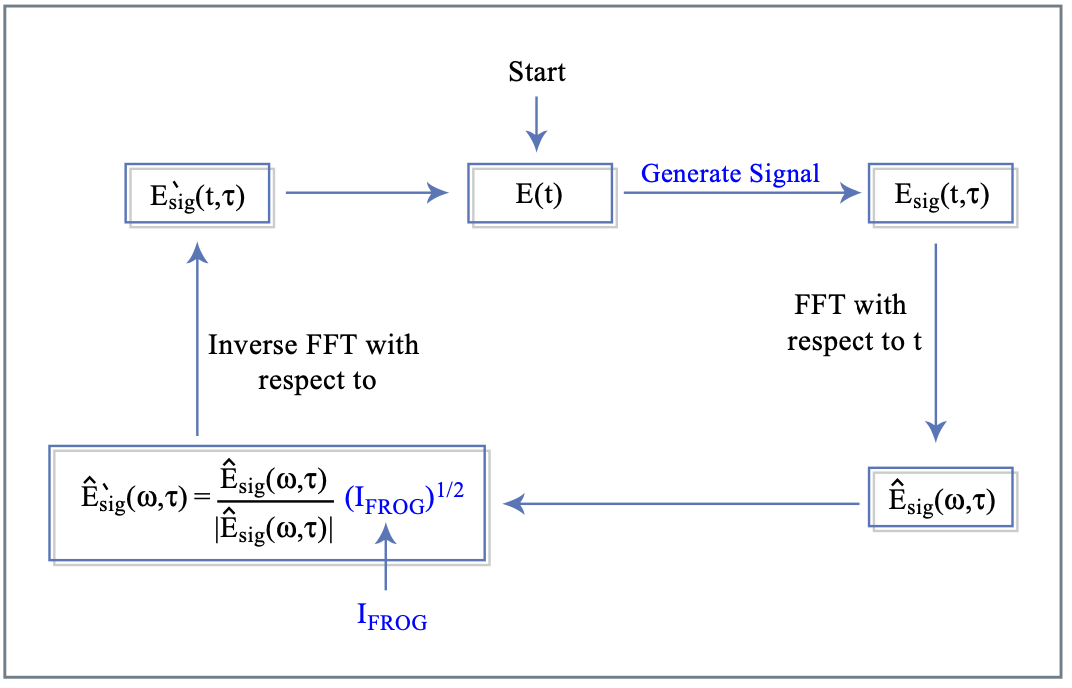
El algoritmo de transformada de Fourier también usado comúnmente en otros problemas de recuperación de fase se muestra esquemáticamente en la Figura 10.16
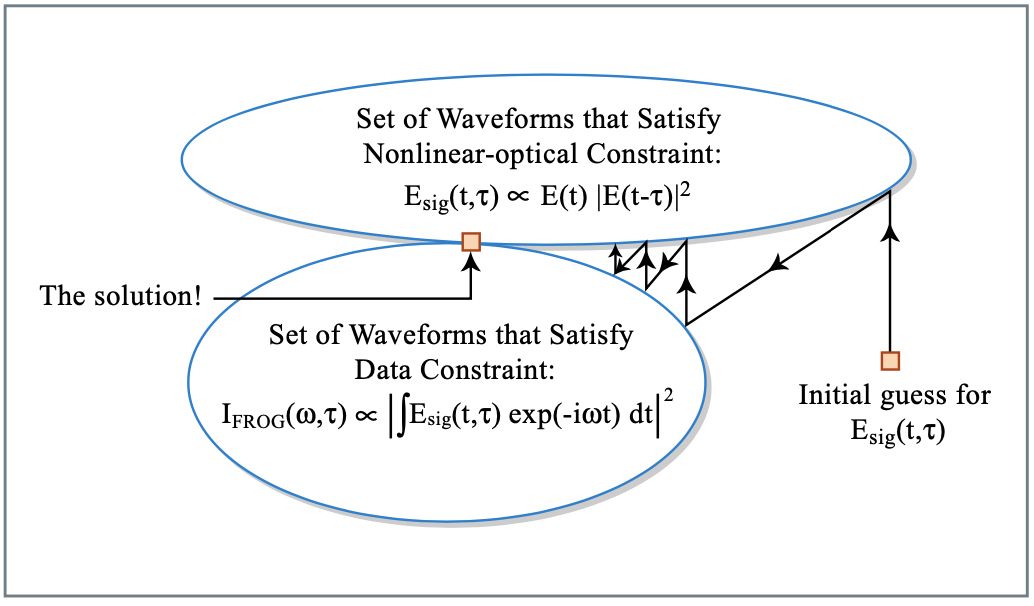
Proyecciones Generalizadas
El campo de señal\(E_{sig}(t, \tau)\) tiene que cumplir dos restricciones, las cuales definen conjuntos ver Figura 10.17. La intersección entre ambos conjuntos da como resultado rendimientos\(E(t)\). Al moverse al punto más cercano en un conjunto de restricciones y luego al otro produce convergencia a la solución, si los dos conjuntos o convexos. Desafortunadamente, las restricciones FROG no son convexas. Sin embargo, el algoritmo funciona sorprendentemente bien. Para mayor información consultar con referencia [5].
RANA Segunda Armónica
Hasta el momento solo discutimos PG-FROG. Sin embargo, si elegimos una\(\chi^{(2)}\) no linealidad, por ejemplo SHG, y establecemos el campo gating-field igual a una copia del pulso\(g(t) \equiv E(t)\), estamos midiendo en eq. (\(\ref{eq10.3.1}\)) la señal de autocorrelación espectralmente resuelta. Los marginales del rastro de ranas medido tienen las siguientes propiedades
\[\int_{-\infty}^{\infty} S_F (\tau, \omega) d\omega \propto \int_{-\infty}^{\infty} |E(t)|^2 \cdot |g(t - \tau)|^2 dt = I_{AC} (\tau). \nonumber \]
\[\int_{-\infty}^{\infty} S_F (\tau, \omega) d\tau \propto \left|\int_{-\infty}^{\infty} \hat{E} (\omega) \cdot \hat{G} (\omega - \omega')^2 d\omega' \right| = \left|\hat{E}_{2\omega} (\omega) \right|^2. \nonumber \]
Para el caso, donde\(g(t) \equiv E(t)\), obtenemos
\[\int_{-\infty}^{\infty} S_F (\tau, \omega) d\omega \propto I_{AC} (\tau). \nonumber \]
\[\int_{-\infty}^{\infty} S_F (\tau, \omega) d \tau \propto \left | \hat{E}_{2\omega} (\omega)\right |^2. \nonumber \]
La configuración para medir el rastro de ranas es idéntica a la configuración para medir la función de autocorrelación de intensidad (Figura 10.1) solo el fotodector para el segundo armónico es reemplazado por un espectrómetro (Figura 10.18).
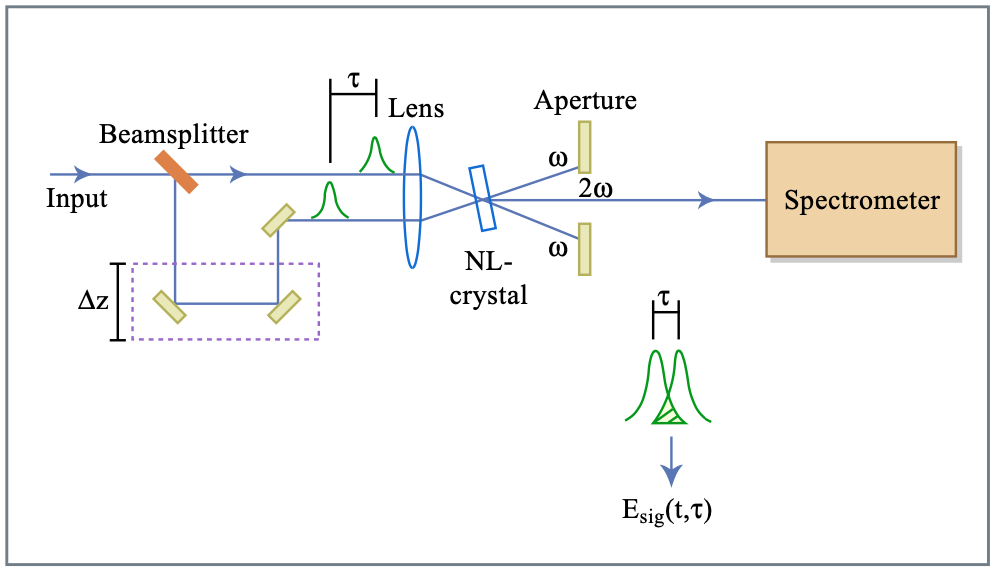
Figura por MIT OCW.
Dado que la función de autocorrelación de intensidad y el espectro integrado se pueden medir simultáneamente, esto da redundancia para verificar la corrección de todas las mediciones a través de los marginales (10.38, 10.39). La Figura 10.19 muestra la traza SHG-FROG de los pulsos más cortos medidos en la superficie con FROG.
Imagen eliminada debido a restricciones de derechos de autor. Por favor vea:
Baltuska, Pshenichnikov y Wiersma. Revista de Quantum Electronics 35 (1999): 459.
Figura 10.19: Medición de FROG de un pulso láser de 4.5 fs.
Geometrías Frog
La señal de rana Esig .también puede ser generada por una interacción no lineal diferente de SHG o PG, ver tabla 10.20 [5].
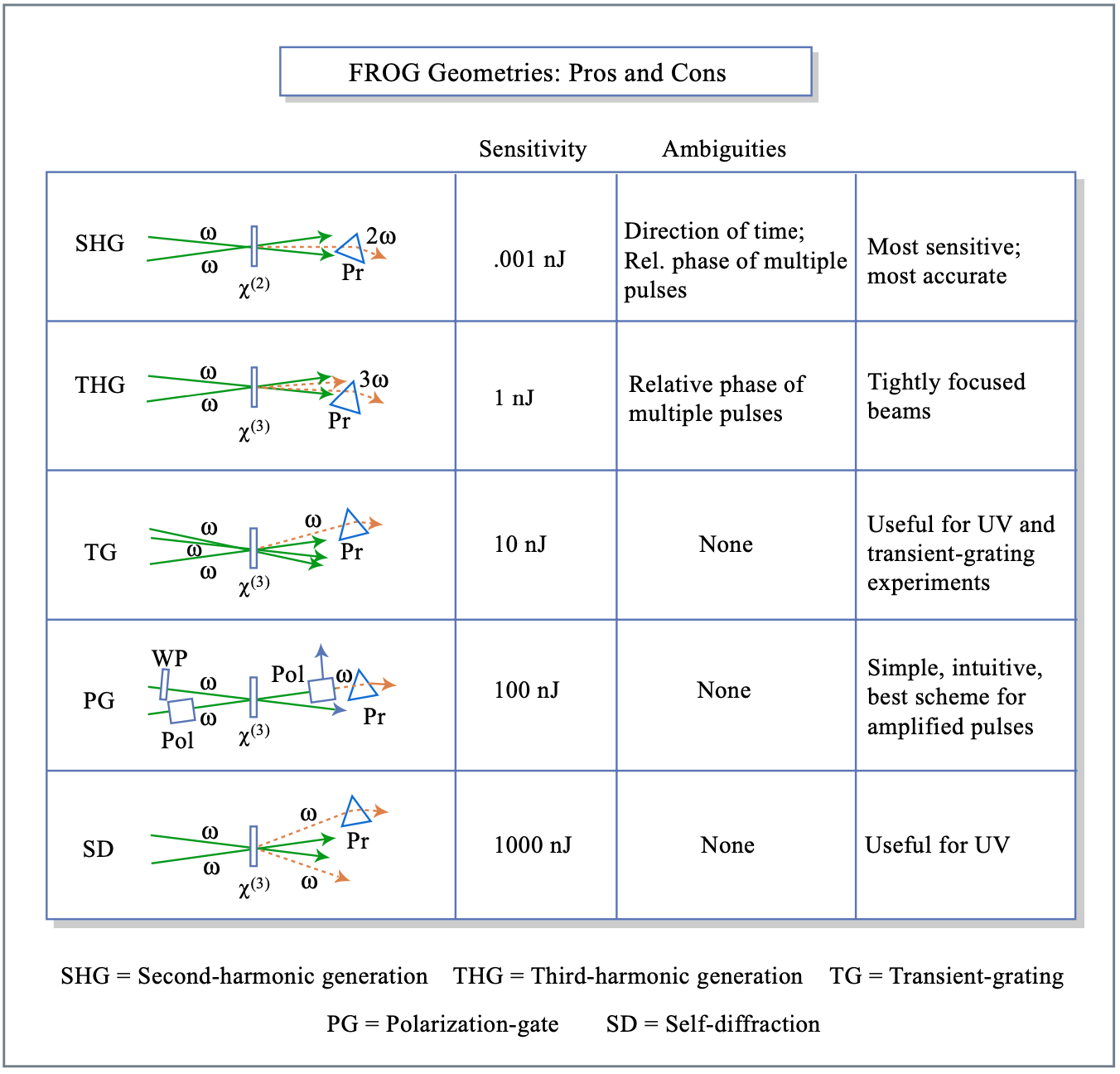
Figura por MIT OCW.


