1.4: Números Complejos
- Page ID
- 85938
En los circuitos de CA, parámetros como voltaje y corriente son vectores, es decir, tienen tanto una magnitud como un desplazamiento de fase o ángulo. Por ejemplo, un voltaje podría ser de “12 voltios en un ángulo de 30 grados” (o de manera más compacta\(12\angle 30^{\circ}\)). Esto se conoce como forma polar o forma de ángulo de magnitud. Como alternativa, un vector se puede romper en forma rectangular, es decir, sus componentes de ángulo recto.
Esto se puede visualizar como un triángulo rectángulo donde la magnitud es la hipotenusa, el ángulo es la rotación por encima o por debajo de la horizontal, el componente horizontal es el lado adyacente al ángulo y el componente vertical es el lado opuesto al ángulo. Esto se muestra en la Figura\(\PageIndex{1}\).
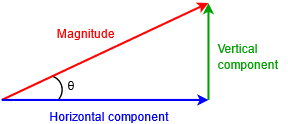
Correctamente, los vectores de voltaje y corriente son números complejos que se encuentran en un plano complejo que consiste en una parte real y una parte imaginaria. El eje horizontal es el eje numérico real y el eje vertical es el eje numérico imaginario. El eje imaginario denota valores multiplicados por el operador imaginario\(j\) (y a menudo referido como\(i\) fuera del análisis eléctrico). El\(j\) operador es la raíz cuadrada de −1. Un ejemplo de tal valor es\(3 + j4\), en otras palabras, 3 unidades a lo largo del eje real horizontal y 4 unidades arriba del eje imaginario vertical. Esto se representa en la Figura\(\PageIndex{2}\).
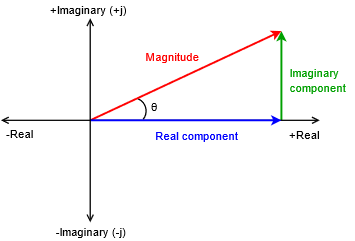
La conversión de una forma a otra se basa en relaciones trigonométricas básicas. Para mayor comodidad, las relaciones entre la magnitud, el ángulo, el componente real y el componente imaginario se reproducen a continuación:
\[\text{Magnitude } = \sqrt{\text{Real}^2 + \text{Imaginary}^2} \label{1.6a} \]
\[\theta = \tan^{−1} \frac{\text{Imaginary}}{\text{Real}} \label{1.6b} \]
\[\text{Real } = \text{ Magnitude } \cos \theta \label{1.6c} \]
\[j\text{Imaginary } = \text{ Magnitude } \sin \theta \label{1.6d} \]
Para sumar o restar cantidades complejas, primero ponerlas en forma rectangular y luego combinar los reales con los reales y los\(j\) términos con los\(j\) términos como en\((3 + j5) + (13 − j1) = 16 + j4\). Estos términos reales e imaginarios deben mantenerse separados. \(3 + j5\)no es igual a 8 (o incluso\(j8\)). Eso sería como decir que mover 3 pies a tu derecha y 5 pies hacia adelante te coloca en la misma ubicación que mover 8 pies a tu derecha (o 8 pies hacia adelante).
La forma directa de multiplicar o dividir valores complejos es ponerlos primero en forma polar y luego multiplicar o dividir las magnitudes. Los ángulos se suman para la multiplicación y se restan para la división. Por ejemplo, los\(12\angle 30^{\circ}\) tiempos\(2\angle 45^{\circ}\) son\(24\angle 75^{\circ}\) mientras se dividen los rendimientos\(6\angle −15^{\circ}\). La necesidad de números complejos se hará más evidente a medida que avanzamos por el material que viene. Es imperativo que hayas dominado la manipulación de valores complejos antes de pasar a capítulos posteriores.
Ejemplo\(\PageIndex{1}\)
Convertir\(15 + j20\) y\(1 k − j2 k\) en forma polar,\(10\angle 45^{\circ}\) y\(0.2\angle −30^{\circ}\) en forma rectangular.
Para las dos primeras conversiones, usa Ecuaciones\ ref {1.6a} y\ ref {1.6b}.
\[\text{Magnitude } = \sqrt{15^2 + 20^2} = 25 \nonumber \]
\[\theta = \tan^{−1} \left( \frac{20}{15} \right) = 53.1^{\circ} \nonumber \]
\[\text{Magnitude } = \sqrt{1 k^2 + (−2 k)^2} = 2.236 k \nonumber \]
\[\theta = \tan^{−1} \left( \frac{−2k}{1 k} \right) = −63.4^{\circ} \nonumber \]
Las respuestas para la primera parte son\(25\angle 53.1^{\circ}\) y\(2.236 k\angle −63.4^{\circ}\).
Para el segundo par de conversiones usa Ecuaciones\ ref {1.6c} y\ ref {1.6d}.
\[\text{Real } = 10 \cos 45^{\circ} = 7.07 \nonumber \]
\[j\text{Imaginary } = 10 \sin 45^{\circ} = j 7.07 \nonumber \]
\[\text{Real } = 0.2 \cos −30^{\circ} = 0.173 \nonumber \]
\[j\text{Imaginary } = 0.2 \sin −30^{\circ} = − j0.1 \nonumber \]
Las respuestas para la segunda parte son\(7.07 + j7.07\) y\(0.173 − j0.1\).
Ejemplo\(\PageIndex{2}\)
a) Sumar\(7 + j8 to + j6\), b) Restar\(5\angle 53.1^{\circ}\) de\(10\angle −45^{\circ}\), c) Dividir\(20\angle 90^{\circ}\) por\(4\angle −50^{\circ}\), d) Multiplicar\(90 + j75\) por\(6 + j10\).
a) Agregar real a real e imaginario a imaginario:\(7 + j14\).
b) Primero convertir los valores en rectangulares:\(3 + j4\) y\(7.07 − j7.07\). Ahora resta el primer par del segundo par:\(4.07 − j11.07\) (o\(11.8\angle −69.8^{\circ}\)).
c) Dividir las magnitudes y restar los ángulos:\(5\angle 140^{\circ}\).
d) Primero convertir los valores en polares:\(117.15\angle 39.8^{\circ}\) y\(11.66\angle 59^{\circ}\). Ahora multiplica las magnitudes y suma los ángulos:\(1.366 k\angle 98.8^{\circ}\).


