3.3: Impedancia paralela
- Page ID
- 85849
Quizás el primer orden del día es determinar valores de impedancia equivalentes para alguna colección de componentes paralelos. Recordemos que el recíproco de la reactancia es la susceptancia,
\[S = \dfrac{1}{X} \label{3.2} \]
y que el recíproco de impedancia es la admitancia,
\[Y = \dfrac{1}{Z} \label{3.3} \]
Las unidades son siemens para cada una. También vale la pena señalar que, debido a la división, los signos se revierten. Por ejemplo, una susceptancia capacitiva tiene un ángulo de +90 grados y si una admitancia compleja tiene un ángulo negativo, entonces la impedancia asociada es inductiva.
La “regla de conductancia” para las combinaciones paralelas estudiadas en el caso DC sigue siendo válida para el caso AC, aunque la generalizamos para impedancias:
\[Z_{total} = \dfrac{1}{\dfrac{1}{Z_1} + \dfrac{1}{Z_2} + \dfrac{1}{Z_3} + \dots + \dfrac{1}{Z_N}} \label{3.4} \]
Cada una de las impedancias individuales presentadas en la Ecuación\ ref {3.4} (es decir\(Z_1\)\(Z_2\),,, etc) puede representar una resistencia simple, una reactancia pura o una impedancia compleja. Además, el acceso directo a la regla producto-suma para dos componentes también sigue siendo válido para los componentes de CA:
\[Z_{total} = \dfrac{Z_1 \times Z_2}{Z_1+Z_2} \label{3.5} \]
Hay un caso especial donde la Ecuación\ ref {3.5} puede ser “problemática”, y ahí es cuando las dos impedancias consisten en una reactancia capacitiva pura y una reactancia inductiva pura, ambas de la misma magnitud. Los dos ítems se cancelarán efectivamente entre sí dejando un denominador de cero y un resultado indefinido. Si bien la combinación teórica “estalla” y se acerca al infinito, en realidad está limitada por resistencias asociadas como\(R_{coil}\), y llega a algún valor finito Esta situación se estudia con gran profundidad en el Capítulo 8, que abarca el concepto de resonancia.
Ejemplo\(\PageIndex{1}\)
Determinar la impedancia de la red mostrada en la Figura\(\PageIndex{1}\).
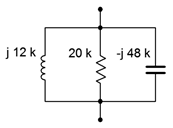
Ecuación\ ref {3.4} sería lo mejor aquí.
\[Z_{total} = \dfrac{1}{\dfrac{1}{Z_1} + \dfrac{1}{Z_2} + \dfrac{1}{Z_3}} \nonumber \]
\[Z_{total} = \dfrac{1}{\dfrac{1}{j 12 k\Omega} + \dfrac{1}{20 k \Omega} + \dfrac{1}{− j 48 k\Omega}} \nonumber \]
\[Z_{total} = 12.49E3\angle 51.3^{\circ} \Omega \nonumber \]
Este resultado podría ser un poco sorprendente para los de ojos afilados. Observe que la magnitud del total es mayor que la magnitud del componente más pequeño (el inductor at\(j12 k\Omega\)). Este nunca sería el caso si estos tres componentes fueran todos resistencias: el resultado tendría que ser menor que el elemento más pequeño del grupo.
La razón de esto es que la reactancia capacitiva cancela parcialmente la reactancia inductiva. Si se utiliza la regla producto-suma (Ecuación\ ref {3.5}) con estos dos componentes, el resultado es\(16E3\angle 90^{\circ}\) o\(j16 k\Omega\). Colocar eso en paralelo con la\(\Omega\) resistencia de 20 k (nuevamente usando la Ecuación\ ref {3.5}) conduce al resultado calculado anteriormente.
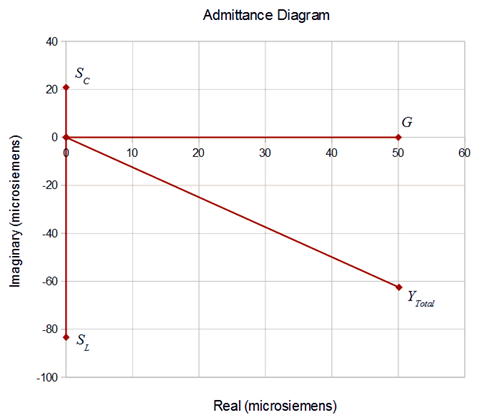
Un diagrama de admisión se ilustra en la Figura\(\PageIndex{2}\). La suma vectorial de la conductancia y susceptancias de los componentes se verifica muy bien.
Los valores de los componentes individuales son:
\[S_L = \dfrac{1}{j 12k \Omega} \approx − j 83.33E-6S \nonumber \]
\[S_C = \dfrac{1}{− j 48k \Omega} \approx j 20.83E-6S \nonumber \]
\[G = \dfrac{1}{20 k\Omega} = 50E-6 S \nonumber \]
\[Y_{total} = \dfrac{1}{12.49E3\angle 51.3^{\circ} \Omega} \approx 80.1E-6\angle −51.3^{\circ} S \nonumber \]
En forma rectangular\(Y_{total} = 50E−6 − j62.5E−6 S\).
Ejemplo\(\PageIndex{2}\)
Determinar la impedancia de la red mostrada en la Figura\(\PageIndex{3}\) a una frecuencia de 10 kHz. Repita esto para una frecuencia de 1 kHz.
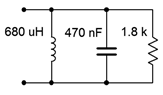
Primero, encuentra las reactancias a 10 kHz. Para el inductor encontramos:
\[X_L = j 2\pi f L \nonumber \]
\[X_L = j 2\pi 10 kHz680 \mu H \nonumber \]
\[X_L \approx j 42.73\Omega \nonumber \]
Y para el condensador:
\[X_C = − j \dfrac{1}{2 \pi f C} \nonumber \]
\[X_C = − j \dfrac{1}{2 \pi 10kHz 470 nF} \nonumber \]
\[X_C \approx − j 33.86\Omega \nonumber \]
Ahora usa la ecuación\ ref {3.4} para combinar los elementos.
\[Z_{total} = \dfrac{1}{\dfrac{1}{Z_1} + \dfrac{1}{Z_2} + \dfrac{1}{Z_3}} \nonumber \]
\[Z_{total} = \dfrac{1}{\dfrac{1}{j 42.73\Omega} + \dfrac{1}{1.8k \Omega} + \dfrac{1}{− j 33.86\Omega}} \nonumber \]
\[Z_{total} = 162.6\angle −84.8^{\circ} \Omega \nonumber \]
En forma rectangular esto es\(14.68 − j161.9 \Omega\). Como la reactancia del condensador es la más pequeña de los tres componentes, domina la impedancia equivalente a esta frecuencia. Al trabajar la fórmula de reactancia capacitiva a la inversa, se puede demostrar que la porción reactiva de se\(− j161.9 \Omega\) puede lograr a esta frecuencia usando una capacitancia de 98.3 nF. Eso significa que a 10 kHz, esta red paralela tiene la misma impedancia que una\(\Omega\) resistencia 14.68 en serie con un condensador de 98.3 nF. En cualquier otra frecuencia esto ya no será cierto, como se ilustrará momentáneamente.
A 1 kHz, la frecuencia se reduce en un factor de diez. Por lo tanto,\(X_L\) será diez veces menor, o aproximadamente\(j4.273 \Omega\). Además,\(X_C\) será diez veces mayor, o aproximadamente\(− j338.6 \Omega\). Ahora dominará la reactancia inductiva.
La nueva impedancia es:
\[Z_{total} = \dfrac{1}{\dfrac{1}{Z_1} + \dfrac{1}{Z_2} + \dfrac{1}{Z_3}} \nonumber \]
\[Z_{total} = \dfrac{1}{\dfrac{1}{j 4.273\Omega} + \dfrac{1}{1.8k \Omega} + \dfrac{1}{− j 338.6\Omega}} \nonumber \]
\[Z_{total} = 4.328\angle 89.9^{\circ} \Omega \nonumber \]
En forma rectangular esto es\(10.4E−3 + j4.328 \Omega\). El resultado es inductivo, lo contrario de lo que vimos a 10 kHz. Utilizando la fórmula de reactancia inductiva, se puede demostrar que a 1 kHz esta red paralela tiene la misma impedancia que una resistencia de 10.4 miliohmios en serie con un inductor de 689\(\mu\) H.


