4.3: Impedancia Serie-Paralelo
- Page ID
- 85811
Las reglas para combinar resistencias, capacitores e inductores en circuitos de CA serie-paralelo son similares a las establecidas para combinar resistencias en circuitos de CC. Obviamente, el primer ítem es determinar las reactancias de los capacitores e inductores. En ese punto, se pueden identificar series simples y combinaciones paralelas. Estas combinaciones se reducen cada una a una impedancia compleja. Una vez completado esto, se vuelve a examinar la red para ver si estas nuevas impedancias complejas pueden identificarse como partes de nuevos subcircuitos en serie o paralelos, y simplificarse. Este proceso se repite hasta que nos quedamos con una sola impedancia compleja. Nuevamente, es útil recordar que los ángulos de fase de los componentes reactivos a veces pueden llevar a resultados sorprendentes, como un subcircuito en serie que tiene una magnitud de impedancia menor que su componente más grande, algo que nunca sucedería con una red compuesta por solo resistencias. La importancia del uso de cálculos vectoriales no puede ser sobrevalorada.
Comencemos con una red RLC serie-paralelo relativamente simple donde ya se han encontrado los valores de reactancia.
Ejemplo\(\PageIndex{1}\)
Determinar la impedancia equivalente de la red mostrada en la Figura\(\PageIndex{1}\).
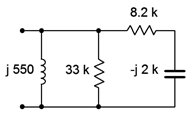
Mirando desde el lado izquierdo, observamos que el inductor y la\(\Omega\) resistencia de 33 k están en paralelo ya que ambos están atados a los mismos dos nodos. Además, podemos ver que el condensador está en serie con la\(\Omega\) resistencia de 8.2 k. Esta combinación en serie es, a su vez, en paralelo con los otros dos componentes paralelos. Así, tendría sentido encontrar primero la combinación de series.
\[Z_{series} = R+(− jX_C ) \nonumber \]
\[Z_{series} = 8.2 k\Omega − j 2k \Omega \nonumber \]
\[Z_{series} = 8440\angle −13.7^{\circ} \Omega \nonumber \]
Ahora colocamos esta nueva impedancia compleja en paralelo con el inductor y la\(\Omega\) resistencia de 33 k.
\[Z_{total} = \frac{1}{\frac{1}{Z_1} + \frac{1}{Z_2} + \frac{1}{Z_3}} \nonumber \]
\[Z_{total} = \frac{1}{\frac{1}{j 550 \Omega} + \frac{1}{33 k\Omega} + \frac{1}{8440\angle −13.7^{\circ} \Omega}} \nonumber \]
\[Z_{total} = 556.8\angle 85.4^{\circ} \Omega \nonumber \]
Claramente, el inductor domina aquí. La resistencia paralela es aproximadamente dos órdenes de magnitud mayor que la reactancia inductiva y tiene un impacto mínimo en una combinación paralela. Además, la impedancia compleja derivada de la combinación de capacitor/resistencia también es considerablemente mayor, y dado que tiene un ángulo de fase negativo (capacitivo), cancela parcialmente la reactancia inductiva. Esto nos deja con una magnitud un poco mayor que la de la reactancia inductiva sola, y con un ángulo de fase desplazado hacia el lado resistivo.
Las combinaciones en serie y paralelas pueden ser mucho más complicadas que las de la red anterior. Las redes de escalera, por ejemplo, cuentan con un conjunto de secciones que cargan otras secciones, lo que resulta en series repetidas y luego simplificaciones paralelas. Ante esta situación, lo mejor es comenzar a trabajar al final más alejado de los nodos de interés. El siguiente ejemplo ilustrará esto a una escala modesta.
Ejemplo\(\PageIndex{2}\)
Determinar la impedancia equivalente de la red mostrada en la Figura\(\PageIndex{2}\).
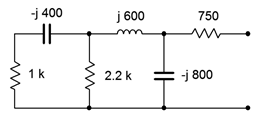
Mirando hacia adentro desde el lado derecho, vemos de inmediato la\(\Omega\) resistencia 750. Esto está en serie con el subcircuito compuesto por los cinco componentes restantes. Este subcircuito puede ser visto como el\(−j800 \Omega \) condensador en paralelo con otro subcircuito que contiene los otros cuatro componentes. Este subcircuito de cuatro componentes consiste en el inductor en serie con otro subcircuito que consiste en las dos resistencias finales y el condensador. Este subcircuito de tres elementos consiste en la\(\Omega\) resistencia de 2.2 k en paralelo con la combinación en serie de la\(\Omega\) resistencia de 1 k y el\(−j400 \Omega \) condensador.
La forma más sensata de abordar esto es comenzar por el extremo izquierdo con la simple combinación de series RC y luego trabajar a la derecha, hacia los nodos de interés. Numeraremos los componentes de izquierda a derecha para su identificación.
\[Z_{left2} = R_1+(− jX_{C1}) \nonumber \]
\[Z_{left2} = 1k \Omega − j 400 \Omega \nonumber \]
\[Z_{left2} = 1077\angle −21.8^{\circ} \Omega \nonumber \]
Ahora colocamos esta impedancia compleja en paralelo con la\(\Omega\) resistencia de 2.2 k. Esto crea un subcircuito de tres elementos que está en serie con el inductor.
\[Z_{left3} = \frac{1}{\frac{1}{R_2} + \frac{1}{Z_{left2}}} \nonumber \]
\[Z_{left3} = \frac{1}{\frac{1}{2.2 k\Omega} + \frac{1}{1077\angle −21.8^{\circ} \Omega}} \nonumber \]
\[Z_{left3} = 734.7\angle −14.7^{\circ} \Omega \nonumber \]
\[Z_{left4} = Z_{left3} +jX_L \nonumber \]
\[Z_{left4} = 734.7\angle −14.7^{\circ} \Omega +j 600\Omega \nonumber \]
\[Z_{left4} = 822.5\angle 30.2 ^{\circ} \Omega \nonumber \]
Este grupo de cuatro está en paralelo con el segundo condensador de\(−j800 \Omega \). Finalmente, llegamos al valor total equivalente colocando el grupo resultante de cinco en serie con la\(\Omega\) resistencia 750.
\[Z_{left5} = \frac{1}{\frac{1}{X_{C2}} + \frac{1}{Z_{left4}}} \nonumber \]
\[Z_{left5} = \frac{1}{\frac{1}{− j 800 \Omega} + \frac{1}{822.5\angle 30.2^{\circ} \Omega}} \nonumber \]
\[Z_{left5} = 813.4\angle −31.3^{\circ} \Omega \nonumber \]
\[Z_{total} = Z_{left5} +R_3 \nonumber \]
\[Z_{total} = 813.4\angle −31.3^{\circ} \Omega +750 \Omega \nonumber \]
\[Z_{total} = 1506\angle −16.3^{\circ} \Omega \nonumber \]
En forma rectangular esto es 1443\(−j422.3 \Omega \), lo que significa que esta red es equivalente a una\(\Omega\) resistencia 1443 en serie con una reactancia capacitiva de\(−j422.3 \Omega \).
Las técnicas de simplificación serie-paralelo no funcionarán para todos los circuitos. Algunas redes como las configuraciones delta o puente requieren otras técnicas que se abordarán en capítulos posteriores.


