5.5: Teorema de transferencia de potencia máxima
- Page ID
- 85826
El concepto de máxima transferencia de potencia en circuitos resistivos de CC se presentó en trabajos anteriores. Si bien maximizar la potencia de carga no es un objetivo de todos los diseños de circuitos, es un objetivo de una parte de ellos y por lo tanto merece una mirada más cercana. En resumen, dada una fuente de voltaje de CA con impedancia interna, como se ve en la Figura\(\PageIndex{1}\), una pregunta útil para hacer es “¿Qué valor de impedancia de carga producirá la cantidad máxima de potencia en la carga?” En el caso de CC, se descubrió que la resistencia de carga debe ser igual a la resistencia de la fuente para lograr la máxima potencia de carga. En el caso de AC las cosas parecen ser mucho más complicadas por la posible presencia de reactancias tanto en la fuente como en la carga.
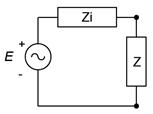
Como actualización del estudio previo, considere el circuito básico representado en la Figura\(\PageIndex{1}\) con fuente\(E\), resistencia interna de fuente\(Z_i\) e impedancia de carga\(Z\). Por el momento, ignoraremos las porciones reactivas y solo describiremos la potencia de carga en términos de la porción resistiva de la carga,\(R\). Para facilitar el trabajo, podemos normalizar la resistencia de origen\(R_i\) a 1\(\Omega\). Al hacer esto,\(R\) también se convierte en un valor normalizado, es decir, ya no representa un valor de resistencia simple sino que representa una relación en comparación con\(R_i\). De esta manera el análisis funcionará para cualquier conjunto de valores fuente. Tenga en cuenta que el valor de\(E\) escalará igualmente la potencia en ambos\(R_i\) y\(R\), por lo que no se necesita un valor preciso, y por lo tanto, también podemos elegir 1 voltio por conveniencia.
La potencia en la carga se puede determinar usando\(I^2 R\) donde\(I = E / (R_i+R)\), cediendo
\[P = \left( \frac{E}{R_i+R} \right)^2 R \nonumber \]
Usando nuestros valores normalizados de 1 voltio y 1\(\Omega\),
\[P = \left( \frac{1}{1+R} \right)^2 R \nonumber \]
Después de expandirnos llegamos a:
\[P = \frac{R}{R^2 + 2 R+1} \label{5.1} \]
Ahora tenemos una ecuación que describe la potencia de carga en términos de la resistencia de carga. Antes de ir más lejos, echa un vistazo a lo que te dice esta ecuación, en general. Es obvio que la potencia máxima no ocurrirá en los extremos. Si\(R = 0\) o\(R = \infty \) (es decir, carga en cortocircuito o abierta) la potencia de carga es cero. El caso de maximización ocurre en algún lugar en el medio. Para encontrar el valor preciso que produce la máxima potencia de carga, la prueba se puede dividir en dos porciones. El primero implica graficar la función y el segundo requiere cálculo diferencial para resolver un valor preciso. Procederemos con la porción gráfica que nos llevará a la respuesta. La prueba más rigurosa de la segunda parte se detalla en el Apéndice C.
La curva de la Ecuación\ ref {5.1} se traza en la Figura\(\PageIndex{2}\). La resistencia de carga normalizada se establece a lo largo de la horizontal y la potencia normalizada (es decir, para una fuente de 1 voltio) se establece a lo largo de la vertical.
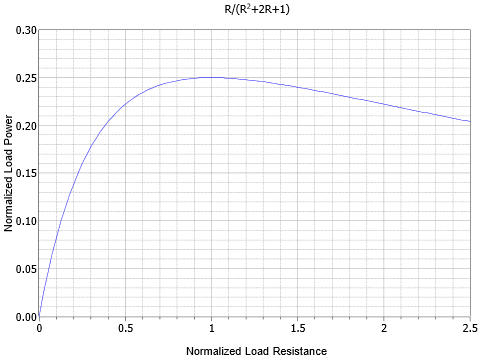
Un examen de la curva de potencia muestra que el pico ocurre en\(R = 1\). En otras palabras, la carga debe ser igual a la resistencia de la fuente. Así, podemos decir que si no hay reactancias involucradas, la potencia de carga máxima se produce cuando la resistencia de carga es igual a la resistencia de la fuente. No importa si la fuente es CC o CA.
La gráfica mostrada en la Figura\(\PageIndex{2}\) es asimétrica pero el concepto de relaciones de resistencia es clave aquí. Esto es más fácil de ver si trazamos la curva de potencia completada usando un eje horizontal logarítmico y también escalamos el eje vertical al 100%, como se muestra en la Figura\(\PageIndex{3}\). El pico es más aparente y la curva es simétrica en forma más que asimétrica. Esto refuerza la idea de que la proporción de las resistencias es lo que importa.
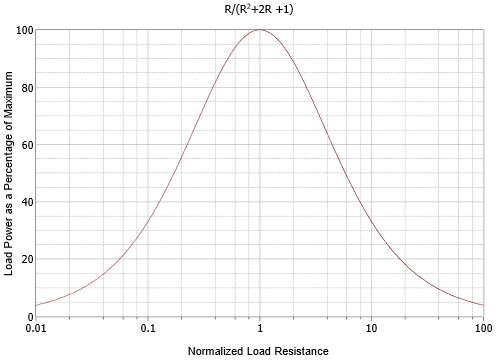
En este punto podemos dirigir nuestra atención a la posible presencia de reactancias tanto en la fuente como en la carga. Resulta que esto no es tan complicado como podría parecer. La clave es que solo las resistencias disipan la potencia, no inductores o condensadores 1. La potencia de carga es proporcional a\(i_{load}^2\), por lo que nuestro objetivo inmediato es maximizar la corriente de carga para cualquier conjunto de resistencias de fuente y carga.
Podemos modificar la ecuación de potencia original agregando un nuevo término,\(X\), que representa la reactancia neta en el circuito. En otras palabras,\(X\) es igual a la suma de las reactancias en la impedancia de la fuente y la impedancia de carga. La potencia en la carga aún se determina utilizando\(I^2 R\), sin embargo, ahora debemos incluir el\(X\) término al calcular la corriente:
\[I = \frac{E}{\sqrt{((R_i+R)^2+X^2 )} \nonumber \]
Esto lleva a una nueva expresión de potencia de carga:
\[P = \left( \frac{E}{\sqrt{((R_i+R)^2+X^2 ) \right)^2 R \label{5.2} \]
Una mirada superficial a la Ecuación\ ref {5.2} muestra que para maximizar\(P\),\(X\) debe ser cero. Una gráfica normalizada de esta ecuación se muestra en la Figura\(\PageIndex{4}\) para\(R = R_i\).
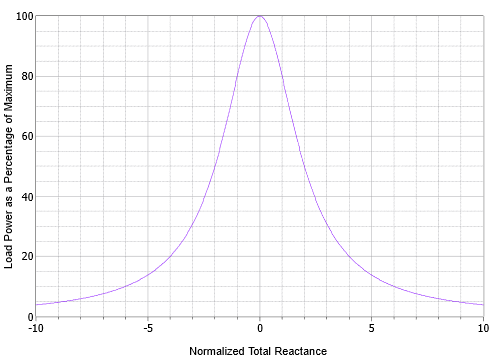
Un solo pico es evidente cuando\(X\) es 0. Esto se puede lograr estableciendo la reactancia de carga igual en magnitud a la reactancia de la fuente pero con el signo opuesto. De esta manera, las reactancias se cancelarán, dejando un circuito puramente resistivo con un valor mínimo, y produciendo así la corriente máxima para ese conjunto de resistencias.
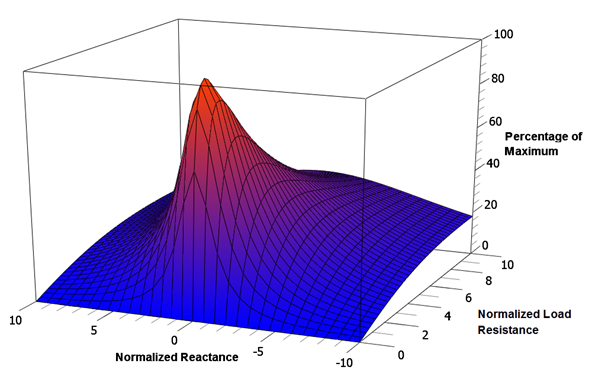
Aquí están involucradas dos variables, por lo que para aclarar aún más la situación, se muestra una gráfica de superficie 3D de potencia normalizada en la Figura\(\PageIndex{5}\). El eje vertical representa el porcentaje de potencia máxima mientras que los ejes frontal y lateral son la reactancia total normalizada y la resistencia a la carga, respectivamente. Un solo pico es evidente aquí y coincide con\(X = 0\) y\(R = 1\). Esto se ve más fácilmente al ver la superficie desde la parte posterior como se muestra en la Figura\(\PageIndex{6}\). Tenga en cuenta que el isocontorno más alto circunda la intersección de\(X = 0\) y\(R = 1\) (es decir,\ R_ {load} = R_i\)).
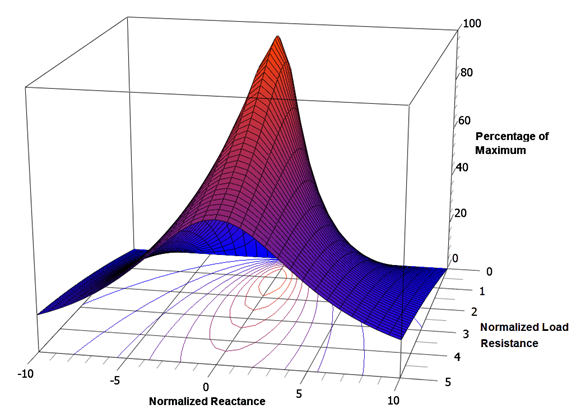
En suma, hemos verificado que las porciones resistivas de la fuente y la impedancia de carga deben ser idénticas y que las porciones reactivas deben ser de la misma magnitud pero de signo opuesto. Esta configuración también se conoce como el conjugado complejo. Por último, podemos afirmar:
\[\text{Maximum load power will be achieved when the load impedance is equal to the complex conjugate of the internal impedance of the driving source.} \nonumber \]
Ningún otro valor de impedancia de carga producirá una mayor potencia de carga. Podemos imaginar dos casos generales, uno con una impedancia de fuente inductiva y otro con una impedancia de fuente capacitiva. Estos se muestran con las cargas adecuadas en la Figura\(\PageIndex{7}\).
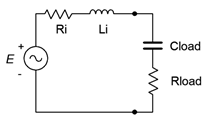
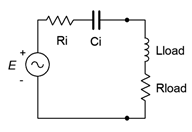
Para lograr la máxima potencia de carga en estos circuitos,\(R_{load} = R_i\) y\(|jX_L| = |−jX_C|\). Tenga en cuenta que\(X_L\) y\(X_C\) no tienen que tener la misma magnitud que\(R_i\).
Si bien el uso del conjugado complejo produce la máxima potencia de carga, no produce la mayor corriente de carga o voltaje de carga posible. De hecho, esta condición produce un voltaje de carga y una corriente de carga que son la mitad de sus máximos. Su producto, sin embargo, está al máximo. Además, la eficiencia a la potencia de carga máxima es solo del 50% (es decir, solo la mitad de toda la energía generada va a la carga y la otra mitad se desperdicia internamente). Valores\(R\) mayores que\(R_i\) lograrán mayor eficiencia pero con una potencia de carga reducida. A veces favorecemos la eficiencia sobre la potencia de carga máxima.
Como cualquier red lineal de un solo puerto puede reducirse a algo así como Figura\(\PageIndex{7}\) usando el teorema de Thévenin, combinar los dos teoremas nos permite determinar las condiciones de potencia máxima para cualquier impedancia en un circuito complejo.
Ejemplo\(\PageIndex{1}\)
Considera el circuito de la Figura\(\PageIndex{8}\). ¿Cuál es la potencia generada en la carga si es igual a 40\(\Omega\)? Además, ¿es esa la potencia máxima que se puede alcanzar, y de no ser así, cuál es la potencia máxima de carga y qué valor de carga se necesitaría?
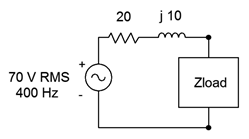
Para encontrar la potencia de carga, primero encuentra la corriente circulante, luego usa la ley de potencia. La impedancia total vista por la fuente es\(20 + j10 \Omega + 40 \Omega\), o\(60 + j10 \Omega\).
\[i = \frac{E}{Z_{total}} \nonumber \]
\[i = \frac{70V}{60\Omega +j 10\Omega} \nonumber \]
\[i = 1.151\angle −9.5^{\circ} A \nonumber \]
Como el voltaje y la corriente están en fase para una resistencia, podemos ignorar el ángulo para el cálculo de potencia.
\[P_{load} = i^2 \times R_{load} \nonumber \]
\[P_{load} = (1.151A)^2 \times 40\Omega \nonumber \]
\[P_{load} \approx 53W \nonumber \]
Esta no es la potencia de carga máxima que se puede lograr porque esta carga no es el conjugado complejo de la impedancia de la fuente. La carga requerida para la potencia de carga máxima se muestra en la Figura\(\PageIndex{9}\).
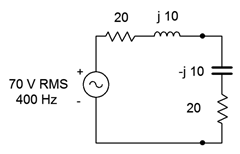
Repetiremos el proceso para encontrar la nueva potencia de carga.
\[i = \frac{E}{Z_{total}} \nonumber \]
\[i = \frac{70 V}{40\Omega} \nonumber \]
\[i = 1.75 \angle 0^{\circ} A \nonumber \]
\[P_{load} = i^2 \times R_{load} \nonumber \]
\[P_{load} = (1.75 A)^2 \times 20 \Omega \nonumber \]
\[P_{load} = 61.25W \nonumber \]
Un método alternativo señala que la impedancia total del nuevo circuito es puramente resistiva y que las resistencias de fuente y carga son idénticas. Por lo tanto, la fuente de voltaje debe dividirse uniformemente entre ellos. En este caso eso son 35 voltios RMS cada uno.
\[P_{load} = \frac{v_R^2}{R_{load}} \nonumber \]
\[P_{load} = \frac{(35 V)^2}{20\Omega} \nonumber \]
\[P_{load} = 61.25W \nonumber \]
Ejemplo\(\PageIndex{2}\)
Para el circuito de la Figura\(\PageIndex{10}\), determinar el valor de\(Z_{load}\) que logrará la máxima potencia de carga y también determinar esa potencia. La fuente de corriente es\(0.1\angle 0^{\circ}\) amperios RMS a 50 kHz.
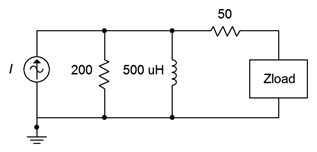
El primer trabajo es determinar la reactancia inductiva a 50 kHz. Recordando eso\(X_L = j2\pi fL\), esto funciona para\(j157 \Omega\). Ahora necesitamos encontrar el equivalente Thévenin. Para encontrarlo\(Z_{th}\) abrimos la fuente actual y miramos hacia atrás desde la carga. Vemos la\(\Omega\) resistencia 50 en serie con la combinación paralela de la\(\Omega\) resistencia 200 y el inductor. La combinación paralela es:
\[Z = \frac{R \times jX_L}{R +jX_L} \nonumber \]
\[Z = \frac{200 \Omega \times ( j 157 \Omega )}{200\Omega +j 157\Omega} \nonumber \]
\[Z = 76.3+j 97.2\Omega \nonumber \]
Por lo tanto,\(Z_{th} = 126.3 + j97.2 \Omega\). El conjugado complejo es\(126.3 − j97.2 \Omega\). La fórmula de reactancia capacitiva se puede usar para determinar el valor de capacitancia apropiado para lograr\(−j97.2 \Omega\).
\[C = \frac{1}{2 \pi f X_C} \nonumber \]
\[C = \frac{1}{2\pi 50 kHz 97.2\Omega} \nonumber \]
\[C = 32.8 nF \nonumber \]
El circuito resultante se muestra en la Figura\(\PageIndex{11}\).
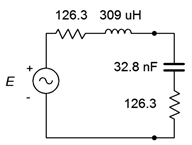
Para encontrar la potencia de carga que necesitamos encontrar\(E_{th}\). El voltaje de salida de circuito abierto es el potencial que aparece a través del par inductor/resistor en la Figura\(\PageIndex{10}\). Esto se debe a que no hay corriente que fluya a través de la\(\Omega\) resistencia 50, y por lo tanto no hay voltaje a través de ella. \(E_{th}\)se puede encontrar a través de la ley de Ohm ya que ya conocemos la impedancia de la rama paralela.
\[E_{th} = i\times Z \nonumber \]
\[E_{th} = 0.1\angle 0^{\circ} A\times (76.3+j 97.2\Omega ) \nonumber \]
\[E_{th} = 12.4\angle 51.9^{\circ} V \nonumber \]
Nuevamente, usando el conjugado complejo, la fuente de voltaje se divide uniformemente entre los componentes resistivos. Como la fuente de corriente se especificó como RMS, también lo será el voltaje equivalente.
\[P_{load} = \frac{v_R^2}{R_{load}} \nonumber \]
\[P_{load} = \frac{(6.2 V)^2}{126.3\Omega} \nonumber \]
\[P_{load} = 304.4mW \nonumber \]
Esto representa la potencia de carga máxima que se puede lograr en este circuito. No olviden, sin embargo, que una cantidad igual de energía es disipada por la fuente. Esto produce una eficiencia de apenas el 50%.
En suma, podemos decir que la potencia de carga máxima se logra cuando la impedancia de carga es igual al conjugado complejo de la impedancia interna de la circuitería que impulsa la carga. Por lo general, esto requiere la aplicación de un equivalente Thévenin o Norton. Por último, aunque la transferencia máxima de potencia es un resultado deseado en algunas situaciones, no es deseable en todas las situaciones. El motivo es uno de eficiencia. A la potencia de carga máxima, la eficiencia es de solo 50%. En contraste, para impedancias de carga que son mayores que la impedancia de la fuente, la potencia de carga disminuirá, sin embargo, la eficiencia aumentará. Una mayor eficiencia es particularmente importante cuando se trata de minimizar el calor y prolongar la vida útil de la batería.
Referencias
1 La alimentación en los circuitos de CA se examina con gran detalle en el Capítulo 7.


