5.6: Conversiones Delta-Y (Pi-T)
- Page ID
- 85848
Ciertas configuraciones de componentes, como las redes puenteadas, no se pueden reducir a una sola impedancia usando técnicas básicas de conversión serie-paralelo. Un método de simplificación consiste en convertir secciones en formas más convenientes. Las configuraciones en cuestión son redes con tres puntos de conexión externos. Debido a la manera en que dibujaron, se les conoce como redes delta y redes Y 1. Estas configuraciones se muestran en la Figura\(\PageIndex{1}\). Tenga en cuenta que la designación terminal de la versión delta está al revés en comparación con las de la configuración Y.
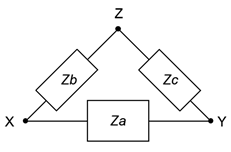
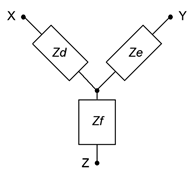
Estas redes se pueden redibujar sin ángulos. De esta forma se les conoce como redes pi (también llamadas “\(\pi\)”) y redes T (también llamadas “tee”) redes. Estas configuraciones se muestran en la Figura\(\PageIndex{2}\).
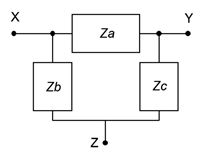
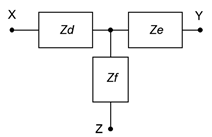
Es posible convertir de un lado a otro entre las redes delta e Y en muchos casos. Es decir, para una red delta dada, puede existir una red Y tal que las impedancias vistas entre los terminales X, Y y Z sean idénticas, y viceversa. En consecuencia, una configuración puede reemplazar a otra para simplificar un circuito más grande. A diferencia de la versión DC, ciertas redes de CA no se pueden convertir utilizando la siguiente técnica (ver el problema de Desafío final para una investigación de esto).
\(\Delta\)-Y Conversión
Un circuito equivalente verdadero presentaría la misma impedancia entre dos terminales cualesquiera que el circuito original. Considere los circuitos de Figura\(\PageIndex{1}\) para el caso descargado (es decir, solo estas redes sin nada más conectado a ellas). Las impedancias equivalentes vistas entre cada par de terminales para el delta y la Y respectivamente son:
\[Z_{XY} = Z_a || (Z_b+Z_c) = Z_d + Z_e \label{5.3} \]
\[Z_{XZ} = Z_b || (Z_a+Z_c) = Z_d + Z_f \label{5.4} \]
\[Z_{ZY} = Z_c || (Z_b+Z_a) = Z_e + Z_f \label{5.5} \]
Supongamos que tenemos la red delta y estamos buscando el equivalente de la red Y. Comenzamos por enfocarnos en el conjunto final de términos para cada una de las tres expresiones (e.g.,\(Z_{XY} = Z_d + Z_e\)). Tenga en cuenta que tenemos tres ecuaciones con tres incógnitas (\(Z_d\),\(Z_e\) y\(Z_f\)). Así, se pueden resolver mediante un proceso de eliminación de término. Si restamos la Ecuación\ ref {5.5} de la Ecuación\ ref {5.3}, podemos eliminar la segunda impedancia (\(Z_e\)) y llegar a una diferencia entre la primera y la tercera impedancia desconocida s (\(Z_d − Z_f\)). Esta cantidad puede entonces ser añadida a la Ecuación\ ref {5.4} para eliminar la tercera impedancia (\(Z_f\)), dejando solo la primera impedancia desconocida (\(Z_d\)).
\[(Z_d + Z_e) − (Z_e + Z_f) = (Z_d − Z_f) = Z_a || (Z_b+Z_c) − Z_b || (Z_a+Z_c) \nonumber \]
\[(Z_d + Z_f) + (Z-d − Z_f) = 2Z_d = 2( Z_b || (Z_a+Z_c) + Z_a || (Z_b+Z_c) − Z_c || (Z_a+Z_b) ) \nonumber \]
Por lo tanto,
\[Z_d = Z_b || (Z_a+Z_c) + Z_a || (Z_b+Z_c) − Z_c || (Z_a+Z_b) \nonumber \]
que, tras simplificar 2, es:
\[Z_d = \frac{Z_a Z_b}{Z_a+Z_b+Z_c} \label{5.6} \]
Del mismo modo, podemos demostrar que
\[Z_e = \frac{Z_a Z_c}{Z_a+Z_b+Z_c} \label{5.7} \]
\[Z_f = \frac{Z_bZ_c}{Z_a+Z_b+Z_c} \label{5.8} \]
Tenga en cuenta que si las magnitudes y ángulos de tres impedancias originales son idénticas, las magnitudes de las impedancias equivalentes Y serán todas un tercio de la magnitud original, y con el ángulo de fase original.
\(\Delta\)Conversión Y
Para el proceso inverso de convertir de Y a delta, comience por anotar las similitudes de las expresiones para\(Z_d\),\(Z_e\) y\(Z_f\) (es decir, Ecuaciones\ ref {5.6} a través de\ ref {5.8}). Si dos de estas expresiones están divididas, una sola ecuación para\(Z_a\),\(Z_b\) o\(Z_c\) resultará. Por ejemplo, usando Ecuaciones\ ref {5.6} y\ ref {5.7}:
\[\frac{Z_d}{Z_e} = \frac{\frac{Z_a Z_b}{Z_a+Z_b+Z_c}}{\frac{Z_a Z_c}{Z_a+Z_b+Z_c}} \nonumber \]
\[\frac{Z_d}{Z_e} = \frac{Z_a}{Z_b}\frac{Z_a}{Z_c} \nonumber \]
\[\frac{Z_d}{Z_e} = \frac{Z_b}{Z_c} \nonumber \]
Por lo tanto,
\[\frac{Z_b}{Z_c} = \frac{Z_d}{Z_e} \nonumber \]
\[Z_b = \frac{Z_c Z_d}{Z_e} \nonumber \]
Este proceso se puede repetir para Ecuaciones\ ref {5.6} y\ ref {5.8} para obtener una expresión para\(Z_a\). Las dos expresiones para\(Z_a\) y luego\(Z_b\) pueden ser sustituidas en la Ecuación\ ref {5.6} para obtener una expresión para\(Z_c\) que utilice solamente\(Z_d\),\(Z_e\) y\(Z_f\). Se sigue un proceso similar\(Z_a\) y\(Z_b\) resulta en:
\[Z_a = \frac{Z_d Z_e + Z_e Z_f + Z_d Z_f}{Z_f} \label{5.9} \]
\[Z_b = \frac{Z_d Z_e+Z_e Z_f +Z_d Z_f}{Z_e} \label{5.10} \]
\[Z_c = \frac{Z_d Z_e+Z_e Z_f +Z_d Z_f}{Z_d} \label{5.11} \]
Si la red Y consta de tres impedancias idénticas, entonces los valores del equivalente delta serán tres veces la magnitud original, la inversa de la situación al convertir de delta a Y.
En suma, las ecuaciones\ ref {5.6},\ ref {5.7} y\ ref {5.8} se pueden usar para convertir una red delta en una red Y, y las ecuaciones\ ref {5.9},\ ref {5.10} y\ ref {5.11} se pueden usar para convertir una red Y en una red delta. A continuación se muestran ejemplos de cómo aplicar esta técnica para domar redes serie-paralelo intratables hasta ahora.
Ejemplo\(\PageIndex{1}\)
Convertir la red de Figure\(\PageIndex{3}\) en su equivalente de configuración delta.
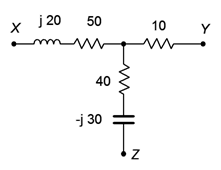
Refiriéndose de nuevo a la Figura\(\PageIndex{2}\), utilice la Ecuación\ ref {5.9} para determinar\(Z_a\).
\[Z_a = \frac{Z_d Z_e + Z_e Z_f +Z_d Z_f}{Z_f} \nonumber \]
\[Z_a = \frac{(50 +j 20\Omega )(10\Omega )+(10\Omega )(40 − j 30\Omega )+(50 +j 20\Omega )(40 − j30\Omega )}{(40 − j 30\Omega )} \nonumber \]
\[Z_a = 65.6 +j 29.2\Omega \nonumber \]
\(Z_b\)y se\(Z_c\) puede determinar de manera similar usando las ecuaciones\ ref {5.10} y\ ref {5.11}:
\[Z_b = 350 − j80 \Omega \nonumber \]
\[Z_c = 54.8 − j37.9 \Omega \nonumber \]
El equivalente se muestra en la Figura\(\PageIndex{4}\).
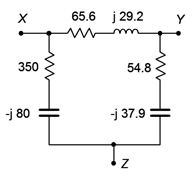
Recuerde, una impedancia compleja siempre se puede expresar en forma rectangular. La forma rectangular se puede expresar directamente como una combinación en serie de una resistencia y una reactancia inductiva o capacitiva. Incluso si las impedancias originales de una red están en forma paralela (o incluso una forma más compleja), el equivalente se puede expresar como una combinación en serie.
Ejemplo\(\PageIndex{2}\)
Determinar\(v_a\) en el circuito de la Figura\(\PageIndex{5}\). Supongamos que la fuente tiene un ángulo de fase de cero grados.
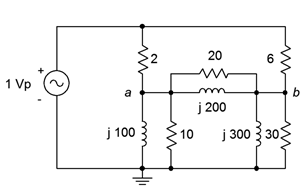
Este circuito no puede simplificarse suficientemente utilizando técnicas básicas serie-paralelo debido a la sección del puente. Los componentes entre y por debajo de los nodos\(a\) y\(b\) comprenden una red delta, como se muestra en la Figura\(\PageIndex{6}\). Si esta red es reemplazada por un equivalente Y, el circuito resultante se reduce a un simple sistema serie-paralelo.
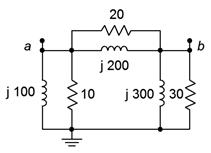
Antes de continuar, sería útil determinar la impedancia de cada una de las secciones paralelas. Para el par más a la izquierda:
\[Z_{left2} = \frac{R \times jX_L}{R +jX_L} \nonumber \]
\[Z_{left2} = \frac{10\Omega \times j 100 \Omega}{10\Omega +j 100 \Omega} \nonumber \]
\[Z_{left2} = 9.9+j 0.99\Omega \nonumber \]
De manera similar, se determina que el par superior es\(19.8 + j1.98 \Omega \) y el par más a la derecha es\(29.7 + j2.97 \Omega \). Refiriéndose de nuevo a la Figura\(\PageIndex{2}\), podemos usar la Ecuación\ ref {5.6} para determinar\(Z_d\).
\[Z_d = \frac{Z_a Z_b}{Z_a + Z_b + Z_c} \nonumber \]
\[Z_d = \frac{(19.8+j 1.98\Omega ) \times (9.9+j 0.99\Omega )}{(19.8+j 1.98\Omega )+(9.9+j 0.99\Omega )+(29.7+j 2.97\Omega ) } \nonumber \]
\[Z_d = 3.3+j 0.33\Omega \nonumber \]
Asimismo, podemos utilizar las Ecuaciones\ ref {5.7} y\ ref {5.8} para determinar\(Z_e\) y\(Z_f\).
\[Z_e = 9.9 + j0.99 \Omega \nonumber \]
\[Z_f = 4.95 + j0.495 \Omega \nonumber \]
El intercambio de la red Y equivalente en el circuito original nos lleva al circuito de la Figura\(\PageIndex{7}\) (la red Y se muestra en azul). Este circuito se puede simplificar directamente para encontrar\(v_a\).
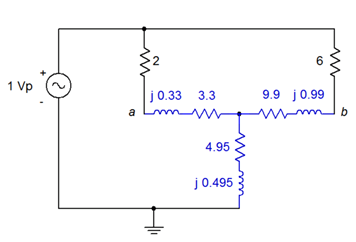
En este circuito equivalente,\(v_a\) es simplemente el voltaje de la fuente de\(1\angle 0^{\circ}\) menos el voltaje a través de la\(\Omega\) resistencia 2. El objetivo inmediato, entonces, es encontrar la corriente a través de esa resistencia. Esto se puede lograr a través de un divisor de corriente una vez que se conoce la corriente fuente. Para encontrar la corriente fuente, necesitamos encontrar la impedancia total de la red. En el lado superior izquierdo,\(Z_d\) está en serie con la 2\(\Omega\) resistencia para un total de\(5.3 + j0.33 \Omega \). Esto es en paralelo con el total del lado superior derecho de\(15.9 + j0.99 \Omega \).
\[Z_{upper} = \frac{Z_{upperleft} \times Z_{upperright}}{Z_{upperleft} +Z_{upperright}} \nonumber \]
\[Z_{upper} = \frac{(5.3 +j0.33\Omega ) \times (15.9 +j 0.99\Omega )}{(5.3 +j 0.33\Omega ) +(15.9 +j 0.99\Omega )} \nonumber \]
\[Z_{upper} = 3.975 +j 0.2475\Omega \nonumber \]
Esto está en serie con la sección inferior de\(4.95 + j0.495 \Omega \) para un total de\(8.956\angle 4.76^{\circ} \Omega \). Usando la ley de Ohm, encontramos la fuente actual:
\[i_{source} = \frac{E}{Z_{total}} \nonumber \]
\[i_{source} = \frac{1\angle 0^{\circ} V}{8.956\angle 4.76^{\circ} \Omega} \nonumber \]
\[i_{source} = 0.1117\angle −4.76^{\circ} A \nonumber \]
Ahora para el divisor de corriente y también la ley de Ohm para la\(\Omega\) resistencia 2.
\[i_{2\Omega} = i_{source} \frac{Z_{upperright}}{Z_{upperright} +Z_{upperleft}} \nonumber \]
\[i_{2\Omega} = 0.1117\angle −4.76^{\circ} A \frac{15.9+j 0.99\Omega}{ (15.9+j 0.99\Omega )+(5.3+j 0.33\Omega ) } \nonumber \]
\[i_{2\Omega} = 83.7E-3\angle −4.76^{\circ} A \nonumber \]
\[v_{2\Omega} = i 2\Omega \times R \nonumber \]
\[v_{2\Omega} = 83.7E-3\angle −4.76^{\circ} A \times 2\Omega \nonumber \]
\[v_{2\Omega} = 0.1675\angle −4.76^{\circ} V \nonumber \]
Finalmente, restamos ese potencial de la fuente para encontrar\(v_a\).
\[v_a = E −v_{2\Omega} \nonumber \]
\[v_a = 1\angle 0^{\circ} V −0.1675\angle −4.76^{\circ} V \nonumber \]
\[v_a = 0.833 \angle 0.95^{\circ} V \nonumber \]
Referencias
1 En algunas fuentes se utiliza la letra griega mayúscula delta (\(\Delta\)) en lugar de deletrear “delta” y la letra Y se deletrea como “wye”. Así, puede encontrarse con la discusión de las redes “\(\Delta\)-Y”, “\(\Delta\)-wye” o “delta-wye”. Todo son las mismas cosas.
2 Este proceso, aunque no particularmente difícil, es algo tedioso. Se trata, como dicen, “dejado como ejercicio para el alumno”.


