8.3: Resonancia paralela
- Page ID
- 85921
Si los tres componentes RLC se colocan en paralelo, como en la Figura\(\PageIndex{1}\), puede resultar un circuito resonante paralelo. Normalmente, sería impulsado por una fuente de corriente como se muestra, aunque esto no es un requisito para la resonancia. La resonancia paralela es un poco más complicada que la resonancia en serie debido a que la resistencia de la bobina en serie no puede agruparse con la resistencia restante del circuito como puede hacerlo con la caja en serie. En otras palabras, la realidad práctica es que tenemos un circuito serie-paralelo donde el inductor es, de hecho, una combinación en serie de la inductancia y la resistencia de la bobina. Resulta que por lo general esta resistencia no puede ser ignorada, aunque sea muy pequeña. Para paliar este problema, es posible encontrar un equivalente paralelo para la reactancia inductiva en serie y la resistencia de bobina asociada. Es decir, necesitamos una serie para transformar en paralelo.
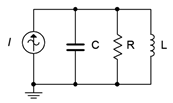
Transformación de inductores serie a paralelo
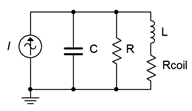
Primero, echemos un vistazo a lo que tenemos en términos prácticos. Un circuito resonante paralelo realista se ilustra en la Figura\(\PageIndex{2}\). Este circuito agrega la resistencia interna de la bobina del inductor al circuito ideal que se muestra en la Figura\(\PageIndex{1}\). Lo que nos gustaría hacer es derivar un medio para encontrar el equivalente paralelo del inductor con su resistencia de bobina. Ciertamente, esto debería ser posible de hacer. Después de todo, es un ejercicio trivial hacer lo contrario; es decir, tomar una combinación paralela de inductor y resistencia y encontrar su equivalente en serie (es decir, expresar la impedancia resultante en forma rectangular). Después de completar el proceso deberíamos tener un circuito equivalente como el que se muestra en la Figura\(\PageIndex{3}\). En este circuito equivalente,\(R\) y\(C\) son los valores del circuito original mientras\(L_{(p)}\) y\(R_{coil(p)}\) son los valores transformados equivalentes paralelos derivados del inductor original. En esta versión, es fácil de combinar\(R\) en paralelo con\(R_{coil(p)}\) para crear una sola resistencia y así enrollar de nuevo en nuestro circuito ideal de Figura\(\PageIndex{1}\).
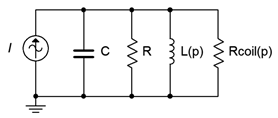
Para la transformada equivalente, consulte la Figura\(\PageIndex{4}\). Comenzamos con una práctica bobina que consiste en una combinación en serie de resistencia y reactancia inductiva,\(R_s + jX_s\). Encontraremos el equivalente paralelo,\(R_p || jX_p\).
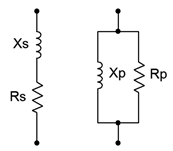
Comenzamos con la regla de conductancia/resistencia recíproca:
\[R_s+jX_s = \frac{1}{\frac{1}{R_p} + \frac{1}{jX_p}} \\ \frac{1}{R_s+jX_s} = \frac{1}{R_p} + \frac{1}{jX_p} \label{8.14} \]
El siguiente paso es aislar las partes reales e imaginarias de la versión en serie. Podemos hacer esto multiplicando el término izquierdo de la Ecuación\ ref {8.10} por el conjugado complejo para llegar a un equivalente:
\[\frac{1}{R_s+jX_s} \frac{R_s − jX_s}{R_s − jX_s} = \frac{R_s}{R_s^2+X_s^2} + \frac{− jX_s}{R_s^2+X_s^2} \nonumber \]
Sustituyendo este equivalente de nuevo en la Ecuación\ ref {8.14} rinde,
\[\frac{R_s}{R_s^2+X_s^2} + \frac{−jX_s}{R_s^2+X_s^2} = \frac{1}{R_p} + \frac{1}{jX_p}\nonumber \]
Por lo tanto,
\[\frac{1}{R_p} = \frac{R_s}{R_s^2+X_s^2} \nonumber \]
\[\frac{1}{jX_p} = \frac{− jX_s}{R_s^2+X_s^2} \nonumber \]
Tomando los resultados recíprocos en:
\[R_p = \frac{R_s^2+X_s^2}{R_s} \label{8.15} \]
\[jX_p = j\frac{R_s^2+X_s^2}{X_s} \label{8.16} \]
Para\(Q\) bobinas altas (\(Q_{coil} \geq 10\))\(X_s \gg R_s\), por lo que podemos aproximar estas como:
\[R_p \approx \frac{X_s^2}{R_s} = Q_{coil} X_s = Q_{coil}^2 R_s \label{8.17} \]
\[jX_p \approx j \frac{X_s^2}{X_s} = jX_s \label{8.18} \]
Así, para un alto\(Q_{coil}\), la reactancia equivalente paralela no cambia desde el valor de la serie y la resistencia equivalente paralela es la resistencia en serie multiplicada por la\(Q\) de la bobina al cuadrado. Curiosamente, la Ecuación\ ref {8.17} muestra que una más pequeña\(R_S\) (que produce una proporcionalmente mayor\(Q_{coil}\)) da como resultado una mayor\(R_P\). Así, el inductor ideal que no tendría resistencia de bobina resulta en una\(R_p\) de infinito. Debido a esta “inversión” resistiva de la transformada serie-paralelo, el circuito paralelo\(Q\) se define como:
\[Q_{parallel} = \frac{R_T}{X_L} \label{8.19} \]
Dónde
\(Q_{parallel}\)es el\(Q\) del circuito resonante paralelo (es decir,\(Q_{circuit}\) para paralelo),
\(R_T\)es la resistencia paralela total\((R_p || R)\),
\(X_L\)es la reactancia a\(f_0\).
Con base en la Ecuación\ ref {8.19} y el desarrollo de la Ecuación\ ref {8.13}, se puede demostrar que:
\[Q_{parallel} = R_T \sqrt{C}{L} \label{8.20} \]
Para\(Q\) circuitos superiores (\(Q_{parallel} \geq 10\)),\(f_0\) se encuentra como en el caso de serie (repitiendo):
\[f_0= \frac{1}{2 \pi \sqrt{LC}} \label{8.2} \]
Para\(Q\) circuitos inferiores, se\(f_0\) reducirá ligeramente debido a que la resistencia transformada depende de la frecuencia. Más sobre esto en una próxima sección.
Impedancia de resonancia paralela
En la Figura se muestra una gráfica de impedancia paralela\(\PageIndex{5}\). El efecto es el inverso del caso de la serie. A bajas frecuencias, la pequeña reactancia inductiva da como resultado una magnitud de baja impedancia con un ángulo de fase positivo (inductivo). A altas frecuencias, la pequeña reactancia capacitiva da como resultado una magnitud de baja impedancia con un ángulo de fase negativo (capacitivo). En resonancia los valores reactivos se cancelan. Esto deja solo el valor resistivo paralelo que produce el pico característico en impedancia. El ángulo de fase es cero, correspondiente a un factor de potencia de unidad.
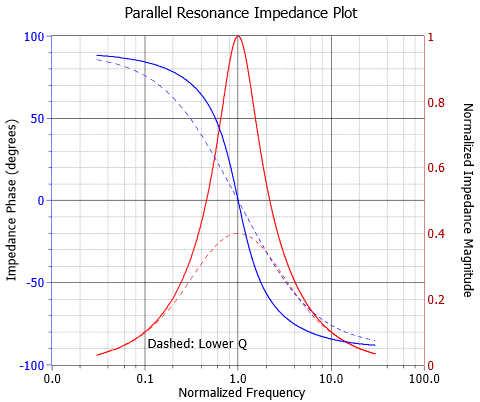
Si el circuito resonante paralelo es accionado por una fuente de corriente, entonces el voltaje producido a través del circuito resonante (a veces denominado circuito de tanque) hará eco de la forma de la magnitud de la impedancia. En otras palabras, discriminará efectivamente las frecuencias altas y bajas y mantendrá solo esas señales en las proximidades de la frecuencia resonante. Este es un método para hacer un filtro de paso de banda. Las frecuencias de media potencia inferior y superior,\(f_1\) y\(f_2\), se encuentran de la misma manera que en la resonancia en serie.
Repetición para mayor comodidad:
\[BW = f_2 − f_1 \label{8.3} \]
\[Q_{circuit} = \frac{f_0}{BW} \label{8.4} \]
\[f_0 = \sqrt{f_1 f_2} \label{8.5} \]
\[\frac{f_0}{f_1} = \frac{f_2}{f_0} \label{8.6} \]
\[k_0 = \frac{1}{2Q_{circuit}} +\sqrt{\frac{1}{4{Q_{circuit}}^2} +1} \label{8.7} \]
\[f_1 = \frac{f_0}{k_0} \label{8.8} \]
\[f_2 = f_0\times k_0 \label{8.9} \]
Para\(Q\) circuitos superiores (\(Q_{circuit} \geq 10\)), podemos aproximar la simetría, y así
\[f_1 \approx f_0 − \frac{BW}{2} \label{8.10} \]
\[f_2 \approx f_0+ \frac{BW}{2} \label{8.11} \]
Por último, vale la pena repetir que para\(Q\) valores relativamente bajos habrá algún desplazamiento de las frecuencias resonantes y de media potencia a partir de las ecuaciones presentadas anteriormente.
Hay algunas similitudes entre la resonancia paralela y la de serie. Al igual que las series, a medida que\(Q\) aumenta el paralelo, la curva de impedancia se vuelve más aguda y el cambio de fase es más abrupto. Además, también vemos un aparente efecto de “\(Q\)amplificación” en circuitos resonantes paralelos, sin embargo, aquí serán las corrientes reactivas las que se incrementarán con relación a la corriente fuente en lugar de las tensiones de los componentes en serie.
Tenga en cuenta que la resistencia paralela puede ser utilizada para bajar el sistema\(Q\) y así ampliar el ancho de banda, sin embargo, el sistema nunca\(Q\) puede ser mayor que el\(Q\) del propio inductor. El inductor establece el límite superior en el sistema\(Q\) y por lo tanto, qué tan estrecho puede ser el ancho de banda. En otras palabras,\(Q_{circuit} \leq Q_{coil}\). Esta es la misma situación que vimos para la resonancia en serie.
Ejemplo\(\PageIndex{1}\)
Para el circuito de la Figura\(\PageIndex{6}\), determinar la frecuencia resonante, las frecuencias de esquina de\(f_1\) y\(f_2\), el ancho de banda y el sistema\(Q\). También encuentra el voltaje del circuito a la frecuencia resonante. \(R_{coil} = 100 \Omega \).
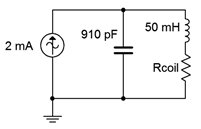
Primero, asumiremos que se trata de un\(Q (\geq 10)\) circuito alto.
\[f_0= \frac{1}{2\pi \sqrt{LC}} \nonumber \]
\[f_0= \frac{1}{2 \pi \sqrt{50 mH910 pF}} \nonumber \]
\[f_0=23.6 kHz \nonumber \]
\[X_L = 2\pi f L \nonumber \]
\[X_L = 2\pi 23.6kHz 50 mH \nonumber \]
\[X_L = 7.41k \Omega \nonumber \]
\[Q_{coil} = \frac{X_L}{R_{coil}} \nonumber \]
\[Q_{coil} = \frac{7.41k \Omega}{100 \Omega} \nonumber \]
\[Q_{coil} = 74.1 \nonumber \]
El equivalente paralelo de la resistencia de la bobina es:
\[R_p = R_{coil} Q_{coil}^2 \nonumber \]
\[R_p = 100\Omega 74.1^2 \nonumber \]
\[R_p = 549.5 k\Omega \nonumber \]
No hay otra resistencia en paralelo con el inductor y el condensador, por lo tanto la resistencia paralela equivalente\(R_p\),, es la resistencia total del circuito,\(R_T\). En consecuencia, el\(Q\) del circuito debe ser el mismo que\(Q_{coil}\). Podemos verificar esto de la siguiente manera:
\[Q_{parallel} = \frac{R_T}{X_L} \nonumber \]
\[Q_{parallel} = \frac{549.5 k \Omega}{7.41 k\Omega} \nonumber \]
\[Q_{parallel} = 74.1 \nonumber \]
Se cumple nuestra suposición inicial de circuito\(Q\) alto.
\[BW = \frac{f_0}{Q_{parallel}} \nonumber \]
\[BW = \frac{23.6 kHz}{74.1} \nonumber \]
\[BW = 318 Hz \nonumber \]
\[f_1 \approx f_0 − \frac{BW}{2} \nonumber \]
\[f_1 \approx 23.6 kHz − \frac{318Hz}{2} \nonumber \]
\[f_1 \approx 23.44 kHz \nonumber \]
\[f_2 \approx f_0 + \frac{BW}{2} \nonumber \]
\[f_2 \approx 23.6 kHz + \frac{318 Hz}{2} \nonumber \]
\[f_2 \approx 23.76 kHz \nonumber \]
Para encontrar el voltaje del circuito en\(f_0\), simplemente multiplique la impedancia resonante de 549.5 k\(\Omega \) por la fuente de 2 mA. Esto produce aproximadamente 1100 voltios.
Simulación por Computadora
El circuito de Ejemplo\(\PageIndex{1}\) se captura en un simulador como se muestra en la Figura\(\PageIndex{7}\).
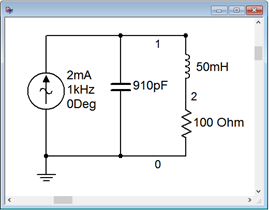
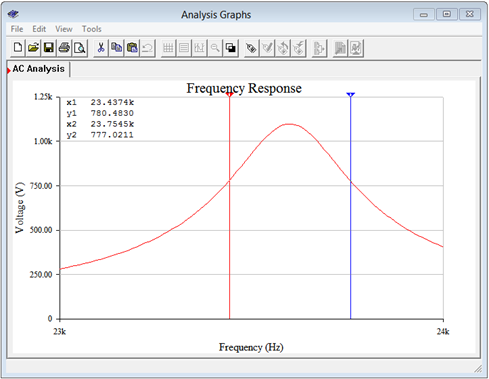
Se ejecuta un análisis de dominio de frecuencia o CA en el circuito, trazando la magnitud de la tensión de la fuente (nodo 1) de 2 kHz a 200 kHz. Esto nos dará aproximadamente un factor de diez a cada lado de la frecuencia resonante. El resultado se muestra en la Figura\(\PageIndex{8}\). La gráfica muestra un pico claro y agudo en la región baja de 20 kHz. Tenga en cuenta que el voltaje pico es de poco más de 1000 voltios, como se predijo. La figura\(\PageIndex{9}\) muestra una versión ampliada de esta gráfica para que podamos verificar con precisión el voltaje pico junto con\(f_1\) y\(f_2\).
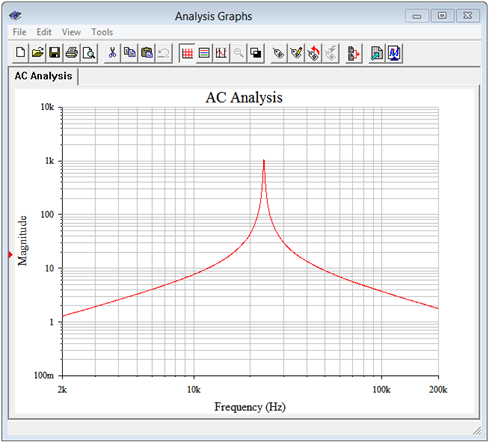
La figura\(\PageIndex{9}\) muestra que el pico es de hecho aproximadamente 1100 voltios. Las\(f_2\) frecuencias\(f_1\) y se encuentran en 0.707 veces este pico, o unos 778 voltios. Para esta tarea se emplean dos cursores de medición. Los valores Y son los voltajes en la intersección del cursor con la curva y los valores X son las frecuencias correspondientes. Podemos ver que los resultados están muy de acuerdo con los cálculos. A niveles de aproximadamente 777 a 780 voltios obtenemos\(f_1\) y\(f_2\) valores de aproximadamente 23.44 kHz y 23.75 kHz, respectivamente.
Ejemplo\(\PageIndex{2}\)
Para el circuito de la Figura\(\PageIndex{10}\), determinar la frecuencia resonante, las frecuencias de esquina de\(f_1\) y\(f_2\), el ancho de banda y el sistema\(Q\). También encuentra el voltaje del circuito a la frecuencia resonante. \(R_{coil} = 100 \Omega \).
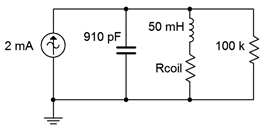
Este circuito es idéntico al del ejemplo anterior con la excepción de una resistencia de\(\Omega \) carga añadida de 100 k. Esto debería bajar el sistema\(Q\) y así ampliar el ancho de banda. También se reducirá la impedancia máxima, lo que provocará una disminución en el voltaje del sistema en resonancia. Algunos parámetros no cambiarán. Incluyen:
\[f_0 = 23.6 kHz \nonumber \]
\[X_L = 7.41 k \Omega \nonumber \]
\[Q_{coil} = 74.1 \nonumber \]
\[R_p = 549.5 k \Omega \nonumber \]
Asumiremos que se trata de un\(Q (\geq 10)\) circuito alto.
Rp está en paralelo con la resistencia de carga de\(R\) producir una resistencia paralela efectiva de\(549.5 k\Omega || 100 k\Omega \), o 84.6 k\(\Omega \).
\[Q_{parallel} = \frac{R_T}{X_L} \nonumber \]
\[Q_{parallel} = \frac{84.6 k \Omega}{7.41k \Omega} \nonumber \]
\[Q_{parallel} = 11.4 \nonumber \]
El circuito\(Q\) está muy reducido pero aún se cumple nuestra suposición inicial\(Q\) de circuito alto. Ahora podemos encontrar el ancho de banda y las frecuencias de esquina.
\[BW = \frac{f_0}{Q_{parallel}} \nonumber \]
\[BW = \frac{23.6 kHz}{11.4} \nonumber \]
\[BW = 2.07kHz \nonumber \]
\[f_1 \approx f_0 − \frac{BW}{2} \nonumber \]
\[f_1 \approx 23.6 kHz − \frac{2.07kHz}{2} \nonumber \]
\[f_1 \approx 22.56 kHz \nonumber \]
\[f_2 \approx f_0 + \frac{BW}{2} \nonumber \]
\[f_2 \approx 23.6 kHz + \frac{2.07kHz}{2} \nonumber \]
\[f_2 \approx 24.64 kHz \nonumber \]
El voltaje del circuito a\(f_0\) se reduce a 84.6 k\(\Omega \) por 2 mA, o 169.2 voltios.
Simulación por Computadora
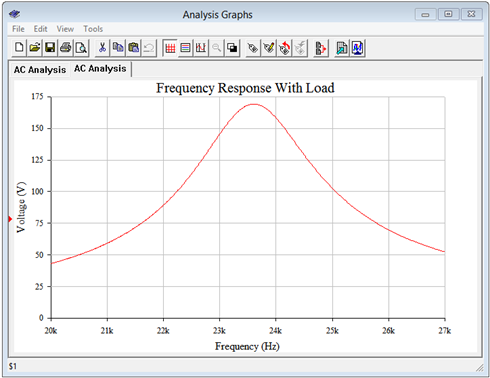
Los resultados de la simulación siguen los del Ejemplo\(\PageIndex{1}\) y se muestran en la Figura\(\PageIndex{11}\). Los resultados concuerdan con los valores calculados. El voltaje pico se ha reducido a aproximadamente 170 voltios, y\(f_1\) y\(f_2\) (encontrado a 0.707 veces el pico, o aproximadamente 120 voltios) son aproximadamente 22.5 kHz y 24.6 kHz, respectivamente.
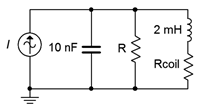
Ejemplo\(\PageIndex{3}\)
Considera el circuito de la Figura\(\PageIndex{12}\) con los siguientes parámetros:\(L\) = 2 mH,\(C\) = 10 nF, y\(Q_{coil}\) = 25. Determinar la frecuencia resonante y un valor para\(R\) tal que el ancho de banda del sistema sea de 3 kHz.
Como de costumbre, asumiremos que se trata de un\(Q (\geq 10)\) circuito alto. Esto ciertamente es cierto para la bobina, aunque tenemos que determinar la frecuencia resonante para determinar la\(Q\) del circuito.
\[f_0 = \frac{1}{2\pi \sqrt{ LC}} \nonumber \]
\[f_0 = \frac{1}{2\pi \sqrt{2mH 10 nF}} \nonumber \]
\[f_0 = 35.59 kHz \nonumber \]
\[Q_{parallel} = \frac{f_0}{BW} \nonumber \]
\[Q_{parallel} = \frac{35.59 kHz}{3 kHz} \nonumber \]
\[Q_{parallel} = 11.86 \nonumber \]
Tenemos alto\(Q\) y podemos continuar 1. En última instancia, necesitamos determinar la resistencia paralela total requerida para lograrlo\(Q\). Antes de que podamos hacer eso tenemos que determinar\(X_L\).
\[X_L = 2\pi f L \nonumber \]
\[X_L = 2\pi 35.59 kHz 2mH \nonumber \]
\[X_L = 447 \Omega \nonumber \]
\[R_T = Q_{parallel} \times X_L \nonumber \]
\[R_T = 11.86\times 447\Omega \nonumber \]
\[R_T = 5.3k \Omega \nonumber \]
\(R_T\)es la combinación paralela de\(R\) y\(R_p\) (el equivalente paralelo de\(R_{coil}\)), así que primero tenemos que encontrar\(R_{coil}\).
\[R_{coil} = \frac{X_L}{Q_{coil}} \nonumber \]
\[R_{coil} = \frac{447\Omega}{25} \nonumber \]
\[R_{coil} = 17.9\Omega \nonumber \]
La resistencia equivalente paralela de\(R_{coil}\) es:
\[R_p = R_{coil} Q_{coil}^2 \nonumber \]
\[R_p = 17.9\Omega 25^2 \nonumber \]
\[R_p = 11.18 k\Omega \nonumber \]
Usando la regla de conductancia, podemos encontrar el valor requerido de\(R\).
\[R = \frac{1}{\frac{1}{R_T} − \frac{1}{R_p}} \nonumber \]
\[R = \frac{1}{\frac{1}{5.3k \Omega} − \frac{1}{11.18 k \Omega}} \nonumber \]
\[R = 10.08 k\Omega \nonumber \]
Por lo tanto, necesitamos usar una\(\Omega \) resistencia de 10.08 k para bajar el circuito\(Q\) lo suficiente para lograr un ancho de banda de 3 kHz. Sin esta resistencia, el ancho de banda será menor a la mitad de lo que se requiere.
Simulación por Computadora
La figura\(\PageIndex{13}\) muestra el diseño terminado del ejemplo anterior capturado en un simulador. Se utiliza una fuente de corriente de 1 mA para mayor comodidad de cálculo.
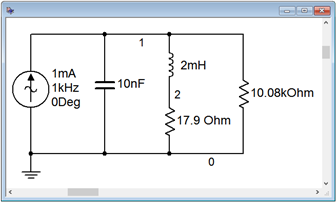
Dado que\(R_T\) es 5.3 k\(\Omega \), la fuente de corriente de 1 mA debe producir 5.3 voltios a la frecuencia de resonancia de 35.59 kHz. Los resultados de un análisis AC se muestran en la Figura\(\PageIndex{14}\).
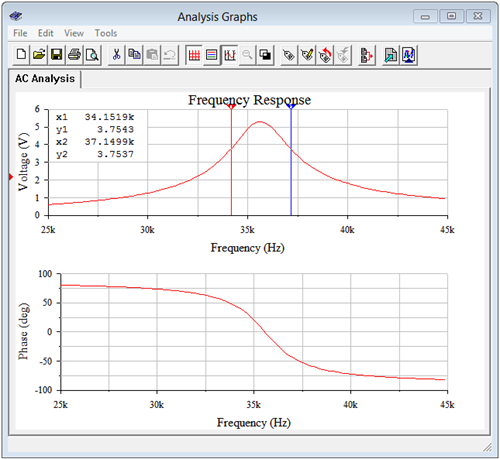
En primer lugar, el\(f_0\) de aproximadamente 35.6 kHz se verifica tanto por el pico en voltaje como por el ángulo de fase que alcanza\(0^{\circ}\) a esta frecuencia, indicando esta última cancelación perfecta entre el inductor y el condensador (es decir, la impedancia del circuito es puramente resistiva y logrando factor de potencia unitaria). Los cursores se utilizan para obtener valores precisos para\(f_1\) y\(f_2\). Estas frecuencias se alcanzan a 0.707 del pico de 5.3 voltios, o alrededor de 3.75 voltios. Las frecuencias son aproximadamente 34.15 kHz y 37.15 kHz, logrando el ancho de banda deseado de 3 kHz.
Resonancia paralela de Q baja
Hay algunos cambios en los cómputos cuando\(Q_{parallel}\) es bajo. Generalmente, esto significa valores por debajo de 10, aunque podríamos pensar en valores entre 5 y 10 como una región de transición donde entran en juego desviaciones de dos puntos porcentuales o menos. Una vez que el circuito\(Q\) cae por debajo de 5, las desviaciones de las\(Q\) ecuaciones altas crecen rápidamente y rápidamente se elevan a porcentajes de dos dígitos. El principal punto de interés aquí es el cambio en\(f_0\).
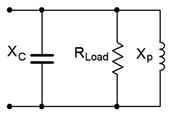
Estas desviaciones son causadas por el hecho de que las aproximaciones utilizadas para las Ecuaciones\ ref {8.17} y\ ref {8.18} ya no son ciertas. Es decir, con\(Q_{coil}\) valores bajos, ya no podemos asumir que el transformado\(X_L\) es lo mismo que el original\(X_L\) (es decir,\(X_p\) y\(X_s\) en la Figura\(\PageIndex{4}\)). Dado este hecho, podemos volver a visitar el circuito RLC paralelo básico, pero esta vez usando el valor exacto de la transformada de inductor serie a paralelo. Esto se muestra en la Figura\(\PageIndex{15}\). \(R_{Load}\)es la resistencia combinada de la red paralela mientras que\(X_p\) es el valor equivalente obtenido de la Ecuación\ ref {8.16} (ligeramente modificada y repetida por conveniencia):
\[X_p = \frac{X^2+R^2}{X} \nonumber \]
\(X\)y\(R\) en esta ecuación están los valores originales de la serie para el inductor. At\(f_0\), las magnitudes de las reactancias son iguales, o\(X_C = X_p\), por lo tanto,
\[X_C = \frac{X^2+R^2}{X} \nonumber \]
Expansión de los rendimientos:
\[\frac{1}{2\pi f_0C} = \frac{(2\pi f_0 L)^2+R^2}{2\pi f_0 L} \nonumber \]
Ahora reorganice y simplifique.
\[\frac{2 \pi f_0 L}{2\pi f_0C} = (2\pi f_0 L)^2+R^2 \nonumber \]
\[\frac{L}{C} = (2\pi f_0 L)^2+R^2 \nonumber \]
\[(2\pi f_0 L)^2 = \frac{L}{C} −R^2 \nonumber \]
\[2\pi f_0 L = \sqrt{ \frac{L}{C} −R^2} \nonumber \]
\[2\pi f_0 = \sqrt{ \frac{1}{LC} − \frac{R^2}{L^2}} \nonumber \]
\[2\pi f_0 = \frac{1}{\sqrt{ LC}} \sqrt{1 − \frac{C R^2}{L}} \nonumber \]
Y finalmente llegamos a:
\[f_0 = \frac{1}{2\pi \sqrt{ LC}} \sqrt{1 − \frac{C R^2}{L}} \label{8.21} \]
Si se desea, podemos tratar el primer término como la frecuencia resonante de serie ordinaria y el segundo término como un coeficiente fraccionario, como en:
\[f_0 = f_{series} k_p \label{8.22} \]
Dónde
\[k_p = \sqrt{1 − \frac{C R^2}{L}} \label{8.23} \]
Usando la ecuación\ ref {8.20}, también se\(k_p\) puede expresar como:
\[k_p = \sqrt{ 1 − \frac{1}{Q^2}} \label{8.24} \]
Examinar la ecuación\ ref {8.23} podría generar cierta preocupación, a saber, ¿qué sucede si el segundo término es mayor o igual a 1? Recuerde, la definición que estamos usando para la resonancia es la frecuencia a la que se cancelan las reactancias, lo que significa que el ángulo de fase es\(0^{\circ}\) (factor de potencia unitaria). Si el segundo término es mayor o igual a 1, el desplazamiento de fase nunca llegará\(0^{\circ}\), y por esa definición, ya no tenemos realmente un circuito resonante.
Exploraremos la realidad de esta situación iniciando con un simple circuito\(Q\) paralelo alto y luego investigaremos los cambios en la respuesta de magnitud y fase a medida\(Q\) que disminuye el. Comenzamos con el circuito de Figura\(\PageIndex{16}\).
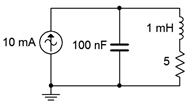
Suponiendo que tenemos circuito alto\(Q\), la frecuencia resonante es:
\[f_0= \frac{1}{2\pi \sqrt{ LC}} \nonumber \]
\[f_0= \frac{1}{2 \pi \sqrt{1 mH100 nF}} \nonumber \]
\[f_0=15.92 kHz \nonumber \]
\[X_L = 2\pi f L \nonumber \]
\[X_L = 2\pi 15.92 kHz 1mH \nonumber \]
\[X_L = 100\Omega \nonumber \]
\[Q_{coil} = \frac{X_L}{R_{coil}} \nonumber \]
\[Q_{coil} = \frac{100\Omega}{5\Omega} \nonumber \]
\[Q_{coil} = 20 \nonumber \]
No hay otras resistencias en el circuito, por lo tanto\(Q_{circuit} = Q_{coil}\) y nuestra suposición inicial es correcta. El circuito se captura en un simulador y se realiza un análisis de CA. Las gráficas resultantes se muestran en la Figura\(\PageIndex{17}\).
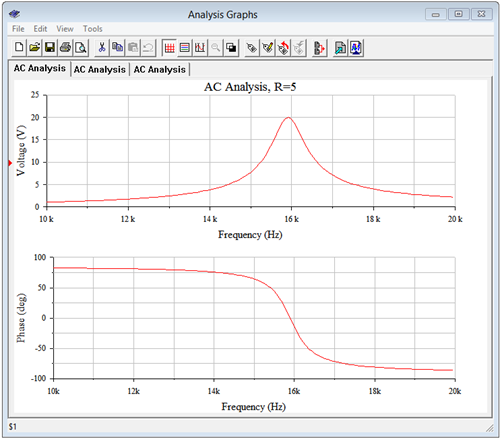
La frecuencia resonante parece estar poco por debajo de 16 kHz, como se predijo. La medición basada en Cursor de la frecuencia a la que se cruza la fase\(0^{\circ}\) produce 15.89 kHz. Esto resulta estar aún más cerca de lo que parece. A pesar del circuito alto\(Q\),\(k_p\) se calculó y como se esperaba está muy cerca de la unidad, es decir, 0.99875. Cuando se multiplica por el ideal\(f_0\) (es decir, usando la Ecuación\ ref {8.22}), llegamos a 15.90 kHz. Partiendo cabellos quizás, pero es bueno saber que la desviación se está encogiendo.
A continuación, la resistencia de la bobina se eleva a 50\(\Omega \), produciendo una\(Q\) de solo 2. La simulación se ejecuta por segunda vez. \(k_p\)cae a 0.866 con esta bajada\(Q\) y debería producir una\(f_0\) de aproximadamente 13.77 kHz. Las parcelas se muestran en la Figura\(\PageIndex{18}\), y se amplían para una mejor visualización. De la gráfica inferior es obvio que la frecuencia donde alcanza la curva\(0^{\circ}\) está justo por debajo de 14 kHz. La medición precisa produce 13.78 kHz, justo en línea con el cálculo teórico.
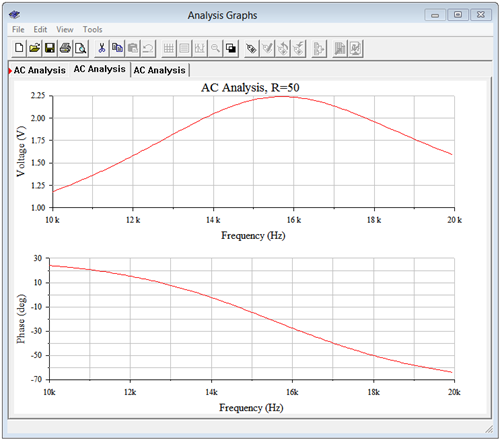
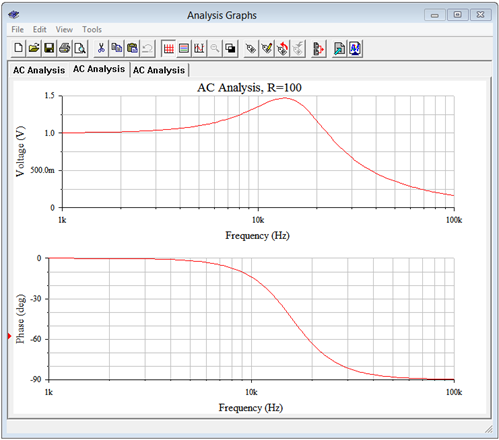
Finalmente, la resistencia de la bobina se incrementa a 100\(\Omega \). Esto baja el circuito\(Q\) a 1 y lo que es más importante,\(k_p\) baja a 0. Las gráficas de simulación resultantes se muestran en la Figura\(\PageIndex{19}\). A primera vista la gráfica de fases se ve similar a la de la Figura\(\PageIndex{17}\), sin embargo, observe que la escala de fase ha cambiado con\(0^{\circ}\) como máximo. De hecho, el desplazamiento de fase nunca alcanza del todo\(0^{\circ}\). Al respecto todavía podemos decir que la\(k_p\) ecuación sigue siendo un predictor preciso.
Definición alternativa para frecuencia resonante paralela
En lugar de definir la frecuencia resonante paralela como el punto donde el factor de potencia es la unidad, es decir, donde\(X_L\) y\(X_C\) tienen la misma magnitud, se puede definir en términos de la frecuencia donde la magnitud de la impedancia es máxima. Para los\(Q\) circuitos altos las dos definiciones producen esencialmente la misma frecuencia, sin embargo, a medida que el circuito\(Q\) disminuye en los dígitos individuales, la frecuencia de impedancia máxima comienza a desviarse tanto de la\(Q\) idealización alta como de la definición general del factor de potencia de unidad. De hecho, la frecuencia de máxima magnitud se sitúa entre las dos. Nos referiremos a esta frecuencia como\(f_{Z-max}\) para evitar confusiones. La fórmula es 2:
\[f_{\text{Z-max}} = f_0 \sqrt{\sqrt{\frac{2}{Q_{circuit}^2} +1} − \frac{1}{Q_{circuit}^2}} \label{8.25} \]
Esta ecuación producirá un valor entre el\(Q\) caso alto ideal y el caso del factor de potencia unitaria. Esto se puede ver en la Figura\(\PageIndex{19}\) donde todavía hay un pico de impedancia (como lo demuestra el pico de voltaje) a pesar de que no\(0^{\circ}\) se alcanza un ángulo de fase de. Además, la frecuencia del pico está por debajo de la del\(Q\) caso alto. La ecuación\ ref {8.25} predice un pico a 13.6 kHz que concuerda con el valor obtenido de la simulación.
Serie combinada y resonancia paralela
Al cerrar nuestra discusión sobre la resonancia podríamos preguntarnos si existen o no ejemplos prácticos y cotidianos de sistemas que exhiben resonancia en serie y paralelo en circuitos serie-paralelo. La respuesta es sí. Un buen ejemplo es el de un altavoz básico de bobina móvil dinámica del tipo visto en el Capítulo 2. Este es un sistema electromecánico y por lo tanto un modelo adecuado tiene que incluir los efectos de elementos tales como las pérdidas mecánicas en el sistema, la masa del cono y similares. Una posibilidad se muestra en la Figura\(\PageIndex{20}\). \(L_{vc}\)y\(R_{vc}\) son la inductancia y resistencia de la bobina de voz. Los componentes restantes modelan otros aspectos del sistema electromecánico. En la Figura se muestra una gráfica de impedancia de un altavoz típico\(\PageIndex{21}\).
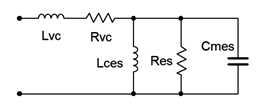
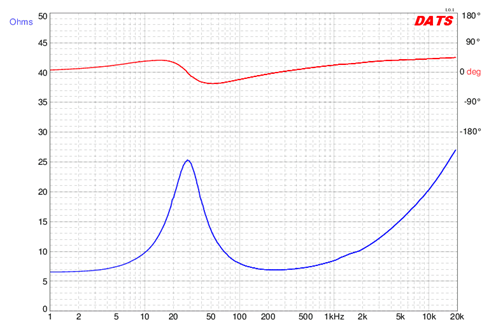
El altavoz de la Figura\(\PageIndex{21}\) es un woofer de tamaño mediano con una impedancia nominal de 8\(\Omega \). Primero, observe la gran variación tanto en la fase como en la magnitud de la impedancia. Los elementos paralelos del modelo producen un pico obvio en impedancia justo por debajo de 30 Hz. Esto se conoce como la resonancia de aire libre y se denota por\(f_s\). Para este dispositivo, la magnitud es más de tres veces el valor nominal. También tenga en cuenta que el ángulo de fase está\(0^{\circ}\) en\(f_s\), y que la fase es positiva (inductiva) por debajo de la frecuencia resonante y negativa (capacitiva) por encima de ella. Este comportamiento se espera de un sistema resonante paralelo. Los elementos de serie del modelo crean la impedancia ascendente que se ve después de la caída. Tenga en cuenta que el ángulo de fase continúa aumentando a medida que aumenta la frecuencia, lo que indica el creciente dominio del elemento inductivo en serie.
Referencias
1 Tenga en cuenta que si este valor hubiera sido mayor a 25 estaríamos atascados por una razón diferente; es decir, que necesitaríamos obtener un inductor de mayor calidad porque no\(Q_{circuit}\) puede ser mayor que\(Q_{coil}\).
2 Para una prueba sin cálculo, véase K. Cartwright, E. Joseph, E. Kaminsky, “Finding the Exact Maximum Impedance Resonant Frequency of a Practical Parallel Resonant Circuit Without Calculus”, Technology Interface International Journal, vol. 11, núm. 1, Otoño/Invierno 2010. [Serie en línea]. Disponible: http://tiij.org/issues/issues/winter...inter_2010.htm [Consultado el 15 de febrero de 2020].


