9.4: Corrección del factor de potencia
- Page ID
- 85952
Como vimos en trabajos anteriores, las cargas reactivas exigen corrientes más altas que las cargas puramente resistivas para una potencia de carga verdadera dada. La relación entre el poder aparente,\(S\), y el verdadero poder,\(P\), es el factor de potencia,\(PF\). El factor de potencia también se puede calcular como el coseno del ángulo de impedancia de carga. Esta situación se mantiene para los sistemas trifásicos. Si una carga trifásica equilibrada tiene un componente reactivo grande, la corriente de línea y la corriente de fase del generador serán más altas de lo necesario. La solución a esto es la corrección del factor de potencia; la introducción de elementos reactivos que contrarrestarán la potencia reactiva de la carga, proporcionando esencialmente una corriente contraria de tal manera que las corrientes reactivas cancelen.
En los sistemas trifásicos la situación se complica potencialmente por el hecho de que la carga se divide en tres partes y puede estar conectada en Y o en delta.
El proceso para tres fases es esencialmente el mismo que para una sola fase, pero con un par de ligeros giros. El primer curso de acción es determinar la potencia reactiva,\(Q\), de la carga. Como estamos tratando con cargas equilibradas, suele ser más fácil concentrarse solo en una sola pierna. Hay dos posibilidades básicas. Primero, si se conoce la reactancia de carga, es una cuestión sencilla determinar la potencia reactiva encontrando la corriente de fase de carga, elevándola al cuadrado y luego multiplicándola por la reactancia de carga. Por el contrario, si la carga se describe en términos de un factor de potencia, la potencia aparente se puede calcular a partir del voltaje y la corriente de fase del generador, y luego el factor de potencia se puede usar para encontrar la potencia reactiva (por ejemplo, encontrar potencia verdadera y luego usar el teorema de Pitágoras). Una vez que se conoce la potencia reactiva, la reactancia requerida se puede encontrar usando la ley de potencia y el voltaje de fase o corriente. Finalmente, se utiliza el valor de reactancia para determinar el valor del componente. Como muchas cargas son inductivas, el componente compensador generalmente será capacitivo. Habrá tres unidades, una por cada tramo de la carga.
Para fines prácticos, el dispositivo de compensación se coloca a través de los terminales de carga en lugar de en serie con él. Esto es cierto tanto si la carga está conectada en Y como si está conectada delta. Es decir, los dispositivos compensadores siempre se colocarán en una configuración delta. Esto es cierto incluso si la carga está conectada en Y. Veremos ambas situaciones en los siguientes dos ejemplos.
Ejemplo\(\PageIndex{1}\)
El sistema Y-delta mostrado en la Figura\(\PageIndex{1}\) tiene un voltaje de fase del generador de 120 voltios RMS a 60 Hz. Determine el factor de potencia, la corriente de fase del generador y la potencia total real y aparente entregada a la carga. También determinar los componentes para corregir el factor de potencia y la nueva corriente de fase del generador.
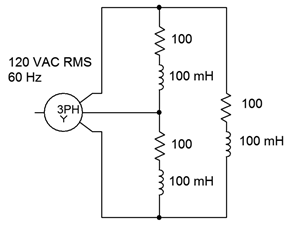
Primero, el factor de potencia es el coseno del ángulo de impedancia. A 60 Hz, la reactancia del inductor de 100 mH es\(−j37.7 \Omega \). Esto está en serie con la resistencia para una impedancia de carga de\(100 −j37.7 \Omega \) o\(106.9\angle 20.66^{\circ}\) por pierna. El coseno de este ángulo es 0.9357.
El voltaje a través de cada tramo de la carga será igual al voltaje de línea.
\[v_{line} = \sqrt{3} \times v_{phase} \nonumber \]
\[v_{line} = \sqrt{3} \times 120 V \nonumber \]
\[v_{line} \approx 207.8V RMS \nonumber \]
Esto producirá una magnitud de corriente de fase de carga de:
\[i_{load} = \frac{v_{phase}}{Z_{load}} \nonumber \]
\[i_{load} = \frac{207.8V}{106.9 \Omega} \nonumber \]
\[i_{load} \approx 1.944A RMS \nonumber \]
Ahora podemos encontrar los poderes de carga.
\[S = 3\times v_{phase}\times i_{phase} \nonumber \]
\[S = 3\times 207.8V\times 1.944 A \nonumber \]
\[S \approx 1212 VA \nonumber \]
\[P = S\times PF \nonumber \]
\[P = 1212VA\times 0.9357 \nonumber \]
\[P \approx 1134 W \nonumber \]
\[Q = S \sin \theta \nonumber \]
\[Q = 1212 VA \sin 20.66^{\circ} \nonumber \]
\[Q \approx 427.6 VAR \nonumber \]
La carga es inductiva, por lo que los componentes de compensación deben ser condensadores. Cada condensador necesita crear 427.6/3 VAR, o 142.5 VAR. La reactancia requerida es:
\[X_C = − j \frac{{v_{phase}}^2}{Q} \nonumber \]
\[X_C = − j \frac{(207.8V)^2}{142.5VAR} \nonumber \]
\[X_C \approx − j 303 \Omega \nonumber \]
Y finalmente, el valor de la capacitancia:
\[C = \frac{1}{2\pi f X_C} \nonumber \]
\[C = \frac{1}{2\pi 60 Hz 303 \Omega} \nonumber \]
\[C \approx 8.75\mu F \nonumber \]
Estos capacitores se colocarían directamente en paralelo con cada pata de la carga y deberían resultar en una reducción de las corrientes del generador y de la línea.
Simulación por Computadora
Para ver el efecto de la corrección del factor de potencia, el circuito utilizado en Ejemplo\(\PageIndex{1}\) se captura en un simulador, como se ilustra en la Figura\(\PageIndex{2}\). El objetivo aquí es mostrar la reducción en la corriente suministrada. Para facilitar esto, no se utiliza la fuente trifásica conectada en Y normal. En cambio, se utilizan tres fuentes sinusoidales individuales, cada una con un desplazamiento de fase adecuado. Una pequeña resistencia\( \Omega \) de detección 1 se inserta en serie con una de las fuentes. El voltaje a través de esta resistencia se mide fácilmente (nodo 7) y sirve como un proxy para la corriente de fase del generador. En comparación con los tamaños de los otros componentes, esta resistencia adicional tendrá un impacto mínimo en el comportamiento general del circuito, quizás cambiando los valores de corriente alrededor del 1% más o menos. Reducir la resistencia a 0.1\( \Omega \) reducirá los errores a niveles insignificantes, pero 1\( \Omega \) es conveniente ya que no se necesita escala y será suficiente para mostrar el efecto de la corrección del factor de potencia en la corriente de la fuente.
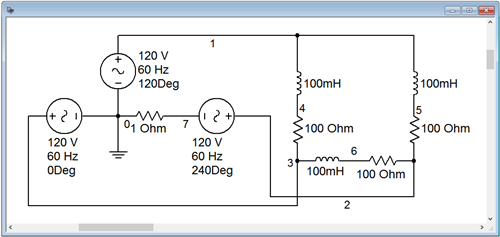
Se ejecuta una simulación transitoria en el circuito, trazando el voltaje en el nodo 7. Esto se muestra en la Figura\(\PageIndex{3}\). Debido a la resistencia de\( \Omega \) detección 1, el valor de voltaje es el mismo que el valor de corriente en amperios. El valor pico de la corriente es de aproximadamente 4.7 amperios. Esto concuerda con el valor calculado de 4.76 amperios (1.944 amperios RMS veces\(\sqrt{2}\) veces\(\sqrt{3}\)). Ahora que se ha establecido una línea base para la corriente, volvemos nuestra atención hacia la versión modificada del circuito con corrección del factor de potencia.
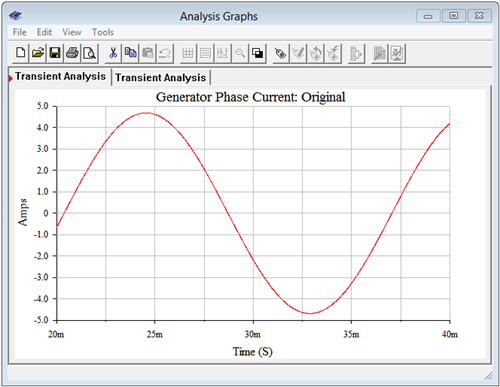
Los tres condensadores de corrección del factor de potencia se agregan en paralelo con las patas de carga existentes (es decir, de línea a línea). Esto se ilustra en la Figura\(\PageIndex{4}\).
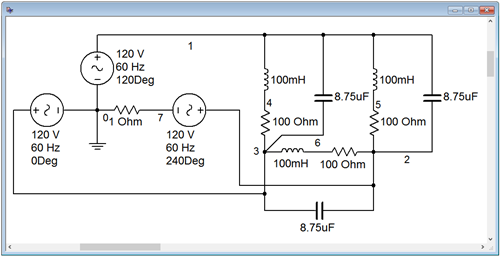
Se repite la simulación transitoria. Los resultados se muestran en la Figura\(\PageIndex{5}\). La corriente pico en esta versión del circuito es de aproximadamente 4.4 amperios. Teóricamente, la corriente debe ser escalada por el factor de potencia, o 0.9357. Como se calculó anteriormente, el valor de la corriente de fase del generador original es de 4.76 amperios pico. Multiplicando eso por el factor de potencia produce aproximadamente 4.45 amperios de pico. La pequeña desviación entre este resultado y la simulación se debe al efecto de la resistencia de\( \Omega \) detección 1.
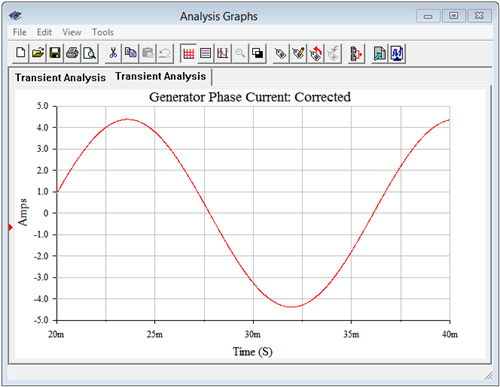
Ejemplo\(\PageIndex{2}\)
El sistema Y-Y mostrado en la Figura\(\PageIndex{6}\) tiene un voltaje de fase del generador de 230 voltios RMS a 50 Hz. La carga consume 900 VA con un factor de potencia de 0.85 rezagado. Determine la corriente de fase del generador. También determine los componentes para corregir el factor de potencia y la nueva corriente de fase del generador una vez que se corrija el sistema.
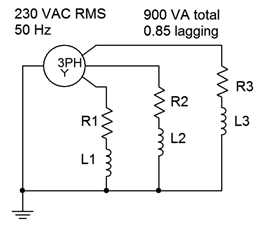
Estamos buscando la corriente de fase del generador así que vamos a descomponer esto en un solo tramo, primero. La potencia aparente total,\(S\), es de 900 VA. Para una sola pierna eso es 300 VA. Este es un sistema Y-Y por lo que la corriente de fase del generador y el voltaje son los mismos que la corriente y voltaje de fase de carga. La corriente se puede encontrar a través de la potencia aparente.
\[i = \frac{S}{v} \nonumber \]
\[i = \frac{300 VA}{230 V RMS} \nonumber \]
\[i \approx 1.304A RMS \nonumber \]
Dado un factor de potencia de 0.85, podemos determinar las potencias reales y reactivas.
\[P = S\times PF \nonumber \]
\[P = 300VA\times 0.85 \nonumber \]
\[P = 255W \nonumber \]
\[Q = \sqrt{S^2−P^2} \nonumber \]
\[Q = \sqrt{(300 VA)^2−(255W)^2} \nonumber \]
\[Q \approx 158 \text{ VAR inductive} \nonumber \]
Para la corrección del factor de potencia, necesitamos 158 VAR capacitivos por pierna para contrarrestar esto. Estos capacitores se colocarán a través de los terminales de carga en una configuración delta. Como tal, verán el voltaje de línea. Para un generador Yconnected, el voltaje de línea es los tiempos de voltaje de fase\(\sqrt{3}\). El resultado aquí es 230 voltios veces\(\sqrt{3}\), o 398.4 voltios RMS. A partir de esto podemos determinar la reactancia requerida.
\[X_C =− j \frac{{v_{phase}}^2}{Q} \nonumber \]
\[X_C =− j \frac{(398.4V)^2}{158 VAR} \nonumber \]
\[X_C \approx − j 1004.6 \Omega \nonumber \]
El valor de capacitancia correspondiente es:
\[C = \frac{1}{2\pi f X_C} \nonumber \]
\[C = \frac{1}{2\pi 50Hz 1004.6 \Omega} \nonumber \]
\[C \approx 3.17\mu F \nonumber \]
Simulación por Computadora
En Ejemplo\(\PageIndex{2}\) calculamos la corriente de fase del generador para ser de 1.304 amperios RMS, lo que equivale a 1.844 amperios pico. Si el circuito corregido es apropiado, entonces la potencia aparente debería caer a la potencia real, o 255 vatios. La corriente de fase del generador resultante debe ser esta potencia dividida por el voltaje de fase del generador, 255/230, o 1.109 amperios RMS. Esto equivale al pico de 1.568 amperios. (Como alternativa, podríamos multiplicar la corriente original por el factor de potencia porque el voltaje es constante).
Para verificar la efectividad de la modificación del circuito, comenzamos capturando el circuito en un simulador, como se muestra en la Figura\(\PageIndex{7}\).
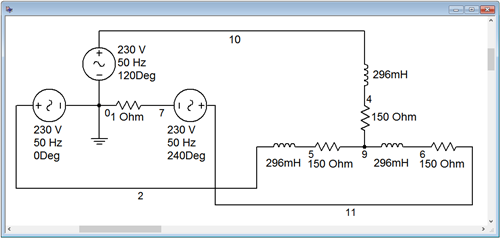
Como en el ejemplo anterior, la fuente se construye a partir de tres generadores sinusoidales discretos en las fases apropiadas. Debajo de uno de ellos, se agrega una resistencia de detección de\( \Omega \) corriente 1 (nodo 7). Este valor no debe producir más de aproximadamente 1% de desviación ya que es un total de dos órdenes de magnitud menor que las otras resistencias del circuito.
Una pregunta interesante para el observador de ojos agudos es cómo se obtuvieron los valores de resistencia de carga e inductor. Esto resulta no ser tan difícil. Ya hemos calculado las potencias verdaderas y reactivas para cada tramo. También conocemos el voltaje de fase de carga (es lo mismo que el generador, 230 voltios, ya que es una conexión Y-Y). Por lo tanto, podemos encontrar los\(X_L\) valores\(R\) y como ya hemos calculado la corriente de carga y podemos usar esto para determinar la impedancia de carga,\(Z\). Se conoce el factor de potencia, y de esto se pueden deducir las partes reales y reactivas.
\[Z = \frac{v_{phase}}{i} \nonumber \]
\[Z = \frac{230 V}{1.304 A} \nonumber \]
\[Z \approx 176 \Omega \nonumber \]
Esta es la magnitud. En aras de la completitud, el ángulo es el arcoseno del factor de potencia, o\(\cos^{-1}(0.85)\), que es de 31.8 grados. La forma más rápida de determinar\(R\) es reconocer que la porción real es la magnitud de la impedancia multiplicada por el factor de potencia:
\[R = Z\times PF \nonumber \]
\[R = 176 \Omega \times 0.85 \nonumber \]
\[R \approx 150 \Omega \nonumber \]
La porción reactiva se puede encontrar a través del teorema de Pitágoras o usando la relación de poder. Luego aplicamos la fórmula de reactancia para encontrar la inductancia.
\[X_L = \frac{Q}{i^2} \nonumber \]
\[X_L = \frac{158VAR}{(1.304 A RMS)^2} \nonumber \]
\[X_L \approx 92.9 \Omega \nonumber \]
\[L = \frac{X_L}{2 \pi f} \nonumber \]
\[L = \frac{92.9 \Omega}{ 2\pi 50 Hz} \nonumber \]
\[L \approx 296 mH \nonumber \]
El resultado de un análisis transitorio se muestra en la Figura\(\PageIndex{8}\). La corriente de fase pico medida es de 1.837 amperios. Esto se compara muy bien con el valor esperado de 1.844 amperios.
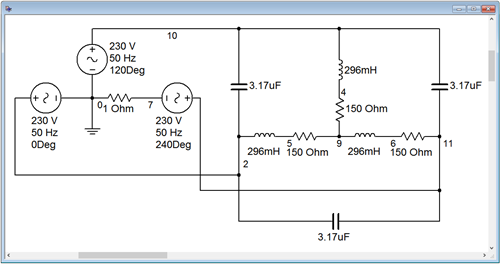
Para la comparación, los capacitores de corrección del factor de potencia se agregan en una configuración delta (a través de las líneas) como se muestra en la Figura\(\PageIndex{9}\).
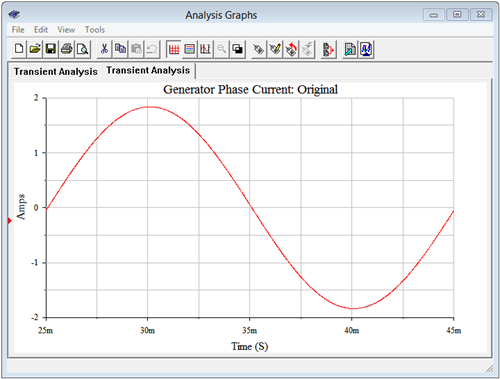
Se ejecuta otra simulación, el resultado que se muestra en la Figura\(\PageIndex{10}\). La corriente pico ha disminuido a 1.56 amperios. Esto es apenas ligeramente inferior al valor esperado de 1.568 amperios pico. Nuevamente, esta pequeña desviación se debe al efecto de la resistencia de detección.