9.6: Ejercicios

Última actualización
Guardar como PDF

Page ID: 85947

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

A menos que se especifique lo contrario, supongamos que las frecuencias del generador son de 60 Hz para

Análisis

1. Como se representa en la Figura\(\PageIndex{1}\), un generador trifásico conectado en delta alimenta una carga conectada delta. El voltaje de fase del generador es de 120 voltios y la carga consta de tres patas de 10\(\Omega\) cada una. Encuentre el voltaje a través de cada tramo de carga, la corriente de línea a través de los cables que conectan la carga al generador y la potencia extraída por la carga.

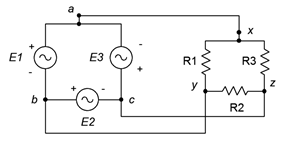
Figura\(\PageIndex{1}\)

2. Haciendo referencia al sistema delta-delta de la Figura\(\PageIndex{1}\), si el voltaje de fase del generador es de 230 voltios y la carga se equilibra con cada pata en 2\(\Omega\), determinar el voltaje de línea, la corriente de línea, la corriente de fase del generador y la corriente de carga.

3. El sistema de la Figura\(\PageIndex{2}\) muestra un generador trifásico conectado en Y que alimenta una carga conectada en Y. Si el voltaje de fase del generador es de 120 voltios y la carga consta de tres patas de 20\(\Omega\) cada una, encuentre el voltaje de línea, la corriente de línea, el voltaje a través de cada tramo de carga y la potencia total extraída por la carga.

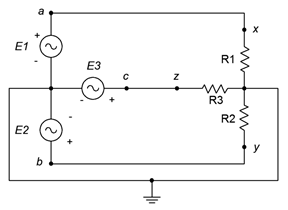
Figura\(\PageIndex{2}\)

4. Haciendo referencia a la Figura\(\PageIndex{2}\), si el voltaje de fase del generador es de 230 voltios y la carga se equilibra con cada pata a 12\(\Omega\), determinar el voltaje de línea, corriente de línea, corriente de fase del generador, corriente de carga, voltaje de carga y potencia de carga total.

5. Como se representa en la Figura\(\PageIndex{3}\), un generador trifásico conectado en delta alimenta una carga conectada en Y. El voltaje de fase del generador es de 120 voltios y la carga consiste en patas balanceadas de 5\(\Omega\) cada una. Encuentre el voltaje en cada tramo de carga, la corriente de línea, la tensión de línea, la corriente de fase del generador y la potencia de carga total.

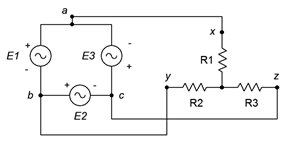
Figura\(\PageIndex{3}\)

6. Haciendo referencia a la Figura\(\PageIndex{3}\), si el voltaje de fase del generador es de 400 voltios y la carga se equilibra con cada pata a 10\(\Omega\), determine el voltaje de línea, la corriente de línea, la corriente de fase del generador, la corriente de carga y el voltaje a través de cada tramo de carga

7. El sistema de la Figura\(\PageIndex{4}\) muestra un generador trifásico conectado en Y que alimenta una carga conectada delta. Si el voltaje de fase del generador es de 120 voltios y la carga consta de tres patas de 60\(\Omega\) cada una, encuentre el voltaje de línea, la corriente de línea, el voltaje a través de cada tramo de carga y la potencia total extraída por la carga.

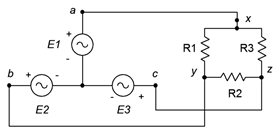
Figura\(\PageIndex{4}\)

8. Haciendo referencia al sistema Y-delta de la Figura\(\PageIndex{3}\), si el voltaje de fase del generador es de 120 voltios y la carga se equilibra con cada pata a 20\(\Omega\), determine la tensión de línea, la corriente de línea, la corriente de fase del generador, la corriente de carga, la tensión a través de cada tramo de carga y la potencia de carga total.

9. Un generador trifásico conectado en delta alimenta una carga conectada delta que consta de tres patas de 10\(\Omega\) en serie con\(j4\)\(\Omega\) reactancia inductiva, como se muestra en la Figura\(\PageIndex{5}\). Si el voltaje de línea es de 208 voltios, encuentre el voltaje a través de cada tramo de carga, la corriente a través de los cables que conectan la carga al generador, y las potencias aparentes y reales extraídas por la carga.

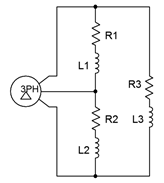
Figura\(\PageIndex{5}\)

10. Dado el sistema delta-delta de la Figura\(\PageIndex{5}\), si el voltaje de fase del generador es de 120 voltios y la carga se equilibra con cada pata en\(20 + j10\)\(\Omega\), determine el voltaje de línea, la corriente de línea, la corriente de fase del generador, la corriente de carga, la tensión a través de cada tramo de carga y la carga total real y aparente poderes.

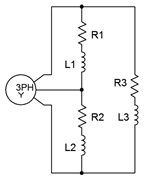
11. Un generador trifásico conectado en Y alimenta una carga conectada en Y que consiste en tres patas de 10\(\Omega\) en serie con\(j4\)\(\Omega\) reactancia inductiva, como se muestra en la Figura\(\PageIndex{6}\). Si el voltaje de línea es de 208 voltios, encuentre el voltaje a través de cada tramo de carga, la corriente de línea y las potencias aparentes y reales extraídas por la carga.

Figura\(\PageIndex{6}\)

12. Dado el sistema Y-Y de la Figura\(\PageIndex{6}\), si el voltaje de línea es de 400 voltios y la carga se equilibra con cada pata en\(100 + j20\)\(\Omega\), determine el voltaje de fase del generador, la corriente de línea, la corriente de fase del generador, la corriente de carga, el voltaje a través de cada tramo de carga y las potencias de carga reales y aparentes totales.

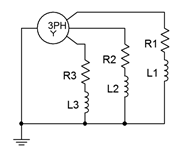
13. El sistema trifásico de la Figura 9.3.3 utiliza un generador conectado en Y que alimenta una carga delta conectada. La carga consta de tres patas de 40\(\Omega\) en serie con\(j30\)\(\Omega\) reactancia inductiva, como se muestra en la Figura 9.32. Si el voltaje de fase del generador es de 230 voltios, encuentre el voltaje de línea, el voltaje a través de cada tramo de carga, la corriente de línea, la corriente de carga y las potencias aparentes y reales extraídas por la carga.

Figura\(\PageIndex{7}\)

14. Dado el sistema Y-delta de la Figura\(\PageIndex{7}\), si el voltaje de línea es de 400 voltios y la carga se equilibra con cada pata en\(80 + j20\)\(\Omega\), determine la tensión de fase del generador, la corriente de línea, la corriente de fase del generador, la corriente de carga, la tensión a través de cada tramo de carga y la carga total real y aparente poderes.

15. Un generador trifásico conectado en delta 208 alimenta una carga conectada en Y que consiste en tres patas de 10\(\Omega\) en serie con\(j4\)\(\Omega\) reactancia inductiva como se muestra en la Figura\(\PageIndex{8}\). Encuentre el voltaje a través de cada tramo de carga, la corriente a través de los cables que conectan la carga al generador y las potencias aparentes y reales extraídas por la carga.

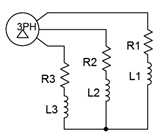
Figura\(\PageIndex{8}\)

16. Dado el sistema delta-Y de la Figura\(\PageIndex{8}\), si el voltaje de línea es de 400 voltios y la carga se equilibra con cada pata en\(120 + j30\)\(\Omega\), determine la corriente de línea, la corriente de fase del generador, la corriente de carga, el voltaje a través de cada tramo de carga y las potencias de carga reales y aparentes totales.

17. Un generador trifásico con conexión delta de 120 voltios alimenta una carga conectada delta que consta de tres patas de 75\(\Omega\) en serie con\(−j10\)\(\Omega\) reactancia capacitiva como se muestra en la Figura\(\PageIndex{9}\). Encuentre el voltaje a través de cada tramo de carga, la corriente a través de los cables que conectan la carga al generador y las potencias aparentes y reales extraídas por la carga.

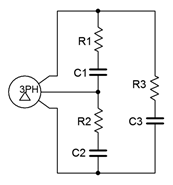
Figura\(\PageIndex{9}\)

18. Un generador trifásico conectado en Y alimenta una carga conectada en Y que consiste en tres patas de 150\(\Omega\) en serie con\(−j20\)\(\Omega\) reactancia capacitiva como se muestra en la Figura\(\PageIndex{10}\). Si el voltaje de fase del generador es de 120 voltios, encuentre el voltaje de línea, el voltaje a través de cada tramo de carga, la corriente de línea y las potencias aparentes y reales extraídas por la carga.

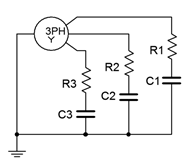
Figura\(\PageIndex{10}\)

Diseño

19. Utilizando el sistema delta-delta del problema 9 y asumiendo que la frecuencia de origen es de 60 Hz, determinar los valores de componentes apropiados para colocar en paralelo con cada tramo de carga para desplazar el factor de potencia a la unidad.

20. Utilizando el sistema Y-Y del problema 11 y asumiendo que la frecuencia de la fuente es de 60 Hz, determinar los valores de componentes apropiados para colocar en paralelo con cada pata de carga para desplazar el factor de potencia a la unidad.

Desafío

21. Utilizando el sistema Y-Y del problema 11 y asumiendo que la frecuencia de la fuente es de 60 Hz, determinar los valores de componente apropiados que se agregarán a la carga con el fin de desplazar el factor de potencia a la unidad. Estos nuevos componentes deben estar en una configuración delta.

Simulación

22. Utilice un análisis transitorio para verificar las relaciones de fase y fase de voltaje de línea en el problema 1.

23. Utilice un análisis transitorio para verificar los resultados calculados para el problema 15.

24. Utilice un análisis transitorio para verificar la solución de diseño al problema 19. Esto se puede lograr asegurando que el voltaje y la corriente en cada tramo de carga (con componentes de corrección añadidos) estén en fase.

25. Utilice un análisis transitorio para verificar la solución de diseño al problema 20. Esto se puede lograr asegurando que el voltaje y la corriente en cada tramo de carga (con componentes de corrección añadidos) estén en fase.