1.2: Estructura atómica

En nuestro esfuerzo por entender el funcionamiento de los semiconductores, una pregunta fundamental que podríamos hacernos es “¿Cuál es la estructura interna de un átomo?” Por favor entienda que no tiene sentido preguntar cómo podría “verse” un átomo porque sus componentes son todos más pequeños que las longitudes de onda de luz más cortas que los humanos pueden ver. En cambio, simplemente necesitamos un modelo para explicar su comportamiento observado.

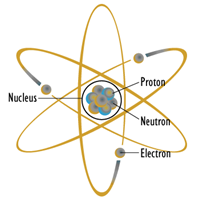
Figura\(\PageIndex{1}\): Modelo atómico planetario: Bonito, conocido y equivocado. Fuente de la imagen (modificada)

Quizás el modelo más prolífico en la imaginación popular es el modelo planetario que se muestra en la Figura\(\PageIndex{1}\). En este modelo, el núcleo, o núcleo, se dibuja en el centro y contiene protones cargados positivamente y neutrones no cargados. Girando alrededor de este núcleo hay electrones cargados negativamente, cada uno siguiendo un camino agradable, regular y plano muy parecido a un planeta alrededor del sol. Desafortunadamente para nosotros, este modelo es marcadamente incorrecto, aunque ha encontrado uso como símbolo para las agencias reguladoras nucleares y una portada de disco de DEVO de la década de 1970.

Antes de llegar a un modelo más preciso y útil, echemos un vistazo más de cerca a los subcomponentes; a saber, el protón, el neutrón y el electrón. En primer lugar, la mayor parte de la masa de cualquier átomo dado proviene de los protones y neutrones. Los protones y neutrones tienen masas similares, aproximadamente 1.67E−24 gramos cada uno. La masa de un electrón es aproximadamente 2000 veces menor. El radio de un protón es de aproximadamente 0.87E−15 metros y la distancia media al electrón más cercano es de aproximadamente 5.3E−11 metros. Esto significa que este electrón está aproximadamente 60,000 veces más alejado del protón que el tamaño de dicho protón. Para poner esto en perspectiva, eso es aproximadamente lo mismo que la relación entre una pelota de golf y una esfera con un radio de 3/4 de milla o 1200 metros. Este sería el caso de un átomo de hidrógeno ya que consiste en un solo protón y electrón. La magnitud de esta relación no es muy diferente para otras sustancias, incluyendo cosas como el carbono cristalino (diamante) y el cuarzo (una molécula de silicio y oxígeno) que son muy duras y sólidas. Si piensas en eso por un momento, te das cuenta de que la idea de “solidez” es en cierto modo una ilusión porque la gran mayoría de lo que llamamos “algo” es realmente solo espacio vacío. Por ejemplo, lo más probable es que estés sentado mientras lees esto. Probablemente sientas tus nalgas presionadas contra la silla. Ambas cosas se consideran sólidas pero a nivel atómico la gran mayoría de ambos elementos es la nada. En realidad, la sensación de solidez es solo el resultado de la interacción de las fuerzas atómicas entre ambas. Entonces, si alguien sugiere que podrías tener un poco de sobra en el departamento de la posterior, puedes informarle que realmente no es nada.

Uno de los principales problemas con el modelo planetario es la idea de que los electrones giran alrededor del núcleo en órbitas estables similares a planetas. Eso simplemente no es cierto. Primero, el electrón habita en una región del espacio 3D, no se mueve simplemente a través de un plano. Segundo, debido al Principio de Incertidumbre de Heisenberg, no podemos trazar con precisión la posición y trayectoria de un electrón dado. Lo mejor que podemos hacer es hacer una gráfica de dónde es probable que esté el electrón. Esto se llama contorno de probabilidad. Imagina que podrías registrar la posición de un electrón con relación al núcleo. Un momento después se registra su nueva posición, un momento después de eso se registra la siguiente posición, y así sucesivamente para miles de mediciones. Si intentabas trazarlos todos, terminarías con una nube de puntos alrededor del núcleo. Esta nube se conoce como orbital. No sabrías cómo llegaba el electrón de una posición a otra pero te darías una idea general de dónde era probable que estuviera. No confundir orbital con órbita (como una órbita planetaria). Son dos bestias distintas.

Existen varios orbitales potenciales. Debido a la física cuántica, sólo se permiten ciertos orbitales. Los niveles permisibles de energía electrónica se agrupan primero en conchas, luego subconchas y finalmente orbitales. Es importante recordar que los orbitales indican el nivel de energía electrónica. Es decir, un orbital superior implica un mayor nivel de energía. Además, los orbitales se llenan primero desde el nivel de energía más bajo hasta el nivel de energía más alto. Estas son ideas importantes que aprovecharemos en futuras discusiones.

Las conchas se denotan por su número cuántico principal,\(n\); 1, 2, 3, etc. Cuanto mayor sea el número, más subconchas puede contener. Las subconchas están organizadas por su forma orbital y están designadas por letras, siendo las cuatro primeras\(s\),\(p\),\(d\), y\(f\). Shell 1 contiene solo subshell\(s\) mientras que shell 2 contiene tipos de subshell\(s\) y\(p\). Shell 3 contiene tipos de subshell\(p\) y\(s\)\(d\), y así sucesivamente.

Así, vemos designaciones como\(1s\),\(2s\) y\(2p\). Estas subconchas también pueden tener variaciones dentro de ellas. Hay una variación sobre\(s\), tres variaciones sobre\(p\), cinco variaciones sobre\(d\), etc. Estas variaciones son los orbitales y cada orbital puede contener un máximo de dos electrones.

Al juntar todo esto, encontramos que el primer caparazón puede contener un máximo de dos electrones: dos en la única\(s\) subcapa orbital (\(1s\)). El segundo caparazón puede contener un máximo de ocho electrones: dos en la\(s\) subcapa (\(2s\)) más dos en cada uno de los tres orbitales de\(p\) subcapa (\(2p\)). De igual manera, el tercer caparazón puede contener un máximo de 18 electrones: dos en\(3s\), seis en\(3p\) y dos en cada uno de los orbitales de las cinco\(d\) subconchas (\(3d\)). Se puede condensar esto en una fórmula simple,\(2n^2\), donde\(n\) está el número de shell.

Figura\(\PageIndex{2}\): Contorno de probabilidad de electrones para orbitales más internos,\(1s\). Fuente de la imagen

La figura\(\PageIndex{2}\) muestra el contorno de probabilidad de electrones del orbital más interno, es decir,\(1s\) (es decir, el principio cuántico número 1, subcapa\(s\)). Como puedes ver, es de forma esférica. El núcleo se encuentra en el centro, oscurecido aquí. Todos los\(s\) orbitales tienen una forma esférica similar aunque las partes internas cambian. \(1s\)es la órbita de menor energía.

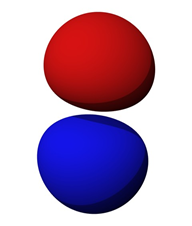
Figura\(\PageIndex{3}\): Contorno de probabilidad de electrones para orbitales\(2p\). Fuente de la imagen

Los orbitales no se limitan a formas esféricas simples. Los orbitales de orden superior pueden tomar una variedad de formas. La figura\(\PageIndex{3}\) muestra el contorno de probabilidad de electrones para los\(2p\) orbitales (recuerde que hay tres\(p\) variaciones, una orientada cada una a lo largo de los ejes X, Y y Z). El núcleo está situado en el pequeño vacío entre los dos lóbulos. Obviamente, esto no se parece en nada a las órbitas elípticas de buen comportamiento de los planetas alrededor del sol. Los contornos de probabilidad pueden ser muy complejos. Para los orbitales más altos, especialmente cuando se combinan con los orbitales inferiores, las combinaciones de contornos pueden llegar a ser reminiscentes de las esculturas de un payaso trastornado formando manadas de animales imaginarios con globos.

Por muy interesantes que sean estos gráficos, resulta engorroso trabajar con ellos. En consecuencia, se requiere un gráfico más funcional. Tal dispositivo es el modelo Bohr, que lleva el nombre del físico danés Niels Bohr. Un ejemplo se muestra en la Figura\(\PageIndex{4}\).

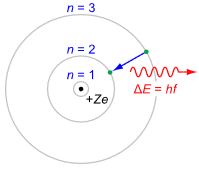
Figura\(\PageIndex{4}\): Modelo genérico de Bohr. Fuente de la imagen

Es importante entender que el modelo de Bohr es una descripción energética del átomo, no un intento de imitar su apariencia física o estructura. El núcleo se coloca en el centro. Está rodeado por anillos concéntricos que representan las conchas de electrones. Cuanto mayor sea el número, mayor será el anillo y mayor será el nivel de energía. Si un electrón pasara de un nivel superior a un nivel inferior, la diferencia de energía se irradia hacia fuera. Esto podría ser en forma de calor o luz. Este es un punto que vale la pena recordar. Por ejemplo, esta transición es lo que hace que los diodos emisores de luz (LEDs) funcionen. También es posible lo inverso, es decir, que al absorber energía, un electrón puede moverse hacia un orbital superior. Este es un concepto igualmente poderoso, como veremos pronto.

Usando el modelo Bohr podemos crear diagramas para representar elementos individuales. Por ejemplo, el cobre tiene un número atómico de 29 lo que significa que tiene 29 protones y 29 electrones. La configuración de la capa electrónica es 2-8-18-1. Es decir, los tres primeros proyectiles están completamente llenos y hay un solo electrón en el cuarto caparazón. Este único electrón externo solo está ligado flojamente y por lo tanto hace que el cobre sea un muy buen conductor. El modelo Bohr para cobre simplemente mostraría cuatro anillos, los tres primeros estando llenos y con un solo electrón en el cuarto anillo.

La figura\(\PageIndex{5}\) muestra el modelo de Bohr de un átomo de Silicio, número atómico 14, con una configuración de carcasa electrónica de 2-8-4. En esta versión, los electrones individuales se dibujan en cada caparazón y el número atómico se indica en el núcleo. Nuevamente, por favor no imaginen esto representando electrones individuales orbitando el núcleo en carriles. Esta es una representación del nivel de energía.

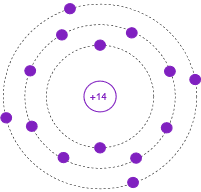
Figura\(\PageIndex{5}\): Modelo Bohr de Silicio.

A menudo, es útil simplificar aún más este modelo omitiendo las carcasas internas rellenas. Además, el número atómico es reemplazado por el número de electrones en la capa más externa, o valencia,. Esto se muestra en la Figura\(\PageIndex{6}\). El caparazón de valencia es particularmente importante ya que da una idea del comportamiento general del material.

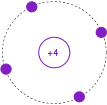
Figura\(\PageIndex{6}\): Modelo Bohr simplificado de Silicio.

Como alternativa, a veces vamos a “enderezar” el modelo de Bohr para que simplemente muestre los niveles de energía gráficamente como líneas o bandas, y sin contar electrones específicos. Esto se representa en la Figura\(\PageIndex{7}\).

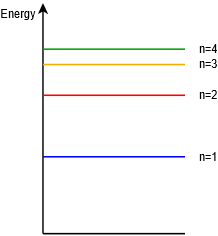
Figura\(\PageIndex{7}\): Diagrama de nivel de energía.