2.4: Modelos de circuitos de diodos
- Page ID
- 83394
Una cosa queda muy clara a partir de la curva característica del diodo: No es un dispositivo lineal bilateral 1, bastante a diferencia de una resistencia. En consecuencia, no podemos utilizar la técnica de superposición para resolver circuitos de diodos a menos que tengamos conocimiento a priori al respecto, es decir, si es o no polarizado hacia delante o hacia atrás. Por ejemplo, podemos imaginar un circuito compuesto por dos fuentes de voltaje, resistencias y un diodo. Por sí misma, una de las fuentes de voltaje podría polarizar hacia adelante el diodo mientras que la otra lo polarizaría hacia atrás. Obviamente, un diodo no puede ser tanto directo como polarizado inverso al mismo tiempo.
Un segundo problema que enfrentamos con el análisis de circuitos es la complejidad añadida de la ecuación de Shockley. Para mayor velocidad y facilidad de cálculo nos parece útil modelar el diodo con elementos de circuito más simples. En la Figura se muestran tres modelos de diodos\(\PageIndex{1}\).
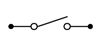
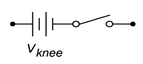
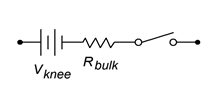
Figura\(\PageIndex{1}\): Modelos de diodos simplificados. De arriba a abajo: primera, segunda y tercera aproximaciones, aumentando en precisión.
La primera aproximación es la más simple de las tres. Trata el diodo como un simple interruptor dependiente: el interruptor se cierra si el diodo está polarizado hacia adelante y se abre si está polarizado hacia atrás. La segunda aproximación agrega el efecto de la tensión directa. \(V_{knee}\)es el potencial de “encendido” requerido para superar el cerro energético. Sería 0.7 voltios para un dispositivo de silicio. La tercera aproximación es la más precisa de las tres. Una mirada cercana a la curva característica de la Figura 2.2.4 muestra que una vez que se alcanza el voltaje de rodilla, la curva no pasa a una línea vertical perfecta. En cambio, queda alguna pendiente positiva, no infinita. Es decir, el voltaje sigue aumentando, aunque modestamente, con mayores incrementos en la corriente. Podemos aproximar este efecto como un pequeño valor resistivo,\(R_{bulk}\). Las tres gráficas I-V correspondientes se muestran en la Figura\(\PageIndex{2}\). Compárelos con la Figura 2.2.6 y anote la precisión creciente.
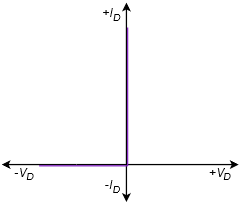
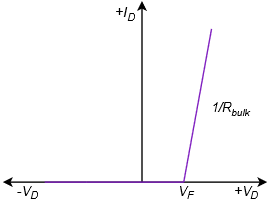
Figura\(\PageIndex{2}\): Curvas I-V para modelos de diodos simplificados. De arriba a abajo: primera, segunda y tercera aproximaciones.
En muchas aplicaciones la segunda aproximación arrojará resultados suficientemente precisos y tenderemos a hacer el mayor uso de la misma. Solo recuerda que estos son modelos de comportamiento; no pienses que hay literalmente fuentes de 0.7 voltios o pequeñas resistencias en los diodos.
Cabe señalar que\(R_{bulk}\) no representa la “resistencia del diodo” per se, más bien, modela un valor mínimo. Realmente no existe tal cosa como una resistencia de diodo singular. Podemos, sin embargo, hablar de la resistencia efectiva de un diodo en un circuito particular tanto en términos de CC como de CA.
La clave para entender este concepto es recordar que la resistencia es una función lineal, una línea recta sobre una gráfica I-V. Por lo tanto, necesitamos encontrar una línea recta “fit” para la curva del diodo. Dos posibilidades se muestran en la Figura\(\PageIndex{3}\).
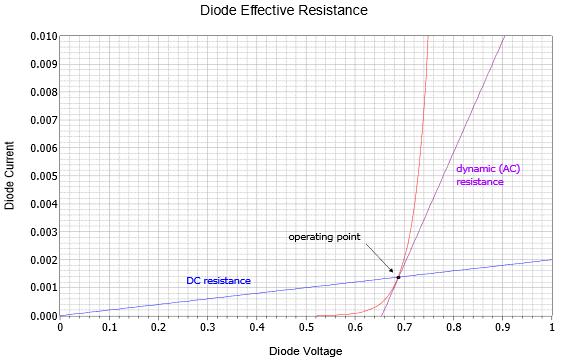
Figura\(\PageIndex{3}\): Resistencia efectiva de diodos para CC y CA.
La curva roja es la curva característica del diodo (se muestran valores arbitrarios de corriente). Para algún circuito de CC particular, una corriente específica fluirá a través del diodo que producirá un voltaje particular, denotado en el gráfico como el punto de operación. Si simplemente calculamos la relación de ese voltaje a la corriente de conducción, terminamos con una resistencia. Esta es la resistencia efectiva de CC del diodo bajo estas condiciones de circuito y está representada por la línea azul. Es decir, el recíproco de la pendiente de la línea azul es la resistencia efectiva de CC. Obviamente, si desplazamos el punto operativo a lo largo de la curva del diodo rojo, la pendiente de la línea azul que se cruza cambia y por lo tanto llegamos a una nueva resistencia de CC. Cuanto mayor sea la corriente, menor será la resistencia efectiva de CC.
En lugar de solo CC, el diodo podría ver una combinación de señales de CC y CA. Visualice esto como la adición de una pequeña variación de CA en la parte superior de la CC. Podemos imaginar el punto de operación moviéndose a lo largo de la curva del diodo rojo, hacia adelante y hacia atrás alrededor del punto de operación. Si dividimos la pequeña variación de voltaje de CA por su variación de corriente alterna asociada, terminamos con la resistencia equivalente de CA, también conocida como resistencia dinámica. Gráficamente, podemos pensar en esto como encontrar la pendiente de una línea que es tangente al punto operativo (la línea púrpura). Esto, de hecho, será un valor promedio a través de la variación de CA. También debería ser evidente que la resistencia efectiva de CA debe ser menor que su contraparte de CC porque la aproximación de CA (línea púrpura) debe ser más pronunciada que la aproximación de CC (línea azul) 2. Es hora de algunos ejemplos ilustrativos.
Ejemplo\(\PageIndex{1}\)
Considere el circuito de resistencia-diodo de la Figura\(\PageIndex{4}\). Supongamos que la fuente de voltaje es de 12 voltios y la resistencia es de 2 k\(\Omega\). Además, supongamos que el diodo es silicio y su resistencia aparente es 10\(\Omega\). Usando las tres aproximaciones de diodos, compute la corriente circulante.
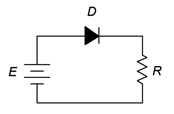
Figura\(\PageIndex{4}\): Esquemática por ejemplo\(\PageIndex{1}\).
Primero, tenga en cuenta que el diodo está polarizado hacia adelante. Este debe ser el caso porque hay un solo voltaje que es mayor que el voltaje de la rodilla y su terminal positivo está conectado al ánodo del diodo. No importa qué aproximación utilicemos, la ley de voltaje de Kirchhoff (KVL) debe ser cierta, por lo que será cuestión de sumar las caídas de voltaje disponibles frente a la (s) resistencia (es).
Usando la primera aproximación:
Aquí asumimos que el diodo es un interruptor cerrado. En consecuencia, todo el voltaje de la fuente debe caer a través de la resistencia única.
\[I = \frac{E}{R} \nonumber \]
\[I = \frac{12V}{2 k\Omega} \nonumber \]
\[I = 6mA \nonumber \]
Usando la segunda aproximación:
En esta instancia incluimos el voltaje de la rodilla.
\[I = \frac{E−V_{knee}}{R} \nonumber \]
\[I = \frac{ 12 V−0.7 V}{2 k\Omega} \nonumber \]
\[I = 5.65mA \nonumber \]
Usando la tercera aproximación:
El más preciso de los tres, incluimos tanto el voltaje de rodilla como la resistencia a granel.
\[I = \frac{ E−V_{knee}}{R+R_{bulk}} \nonumber \]
\[I = \frac{ 12 V−0.7 V}{2 k\Omega+10 \Omega} \nonumber \]
\[I = 5.622mA \nonumber \]
En este caso particular la diferencia entre la segunda y tercera aproximaciones es menor al 1%. También vale la pena señalar que la tercera aproximación predice un voltaje de diodo de poco más de 0.7 voltios (aproximadamente 0.756 voltios) debido al potencial adicional a través de la resistencia masiva.
Ejemplo\(\PageIndex{2}\)
Determine la corriente circulante para el circuito en la Figura\(\PageIndex{5}\). También encuentra los voltajes del diodo y de la resistencia. Supongamos que la fuente de alimentación es de 20 voltios, el diodo es de silicio y la resistencia es de 2 k\(\Omega\).
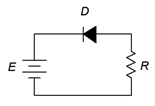
Figura\(\PageIndex{5}\): Esquemática por ejemplo\(\PageIndex{2}\).
Este problema es engañosamente fácil. Tenga en cuenta que el terminal positivo de la fuente está conectado al cátodo. Como no hay otras fuentes en el circuito, el diodo debe ser polarizado en sentido inverso. El modelo para un diodo polarizado inverso es un interruptor abierto y la corriente circulante en un circuito abierto es cero. Por lo tanto, el voltaje de la resistencia también debe ser cero y no se necesitan valores para el voltaje de rodilla y la resistencia masiva. Para satisfacer KVL, el voltaje del diodo será igual a la fuente de 20 voltios (+ a − de cátodo a ánodo).
La única vez que esta no sería el caso es si la tensión de ruptura inversa del diodo es menor que la fuente de 20 voltios. En ese caso, el voltaje del diodo sería igual al voltaje de ruptura con el resto de la tensión de la fuente cayendo a través de la resistencia.
Ejemplo\(\PageIndex{3}\)
Determine la corriente circulante para el circuito en la Figura\(\PageIndex{6}\). También encuentra los voltajes del diodo y de la resistencia. Supongamos que la fuente de alimentación es de 9 voltios, los diodos son de silicio y\(R_1\) = 1 k\(\Omega\),\(R_2\) = 2 k\(\Omega\).
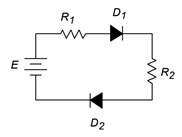
Figura\(\PageIndex{6}\): Esquemática por ejemplo\(\PageIndex{3}\).
Según KVL, la fuente aplicada debe igualar la suma de las caídas de voltaje a través de las resistencias y diodos ya que se trata de un solo bucle. Ambos diodos están polarizados hacia delante (corriente convencional que entra en los ánodos).
\[I = \frac{ E−V_{knee1} − V_{knee2}}{R_1+R_2} \nonumber \]
\[I = \frac{ 9V−0.7V−0.7V}{1k \Omega +2 k\Omega} \nonumber \]
\[I = 2.533mA \nonumber \]
Tenga en cuenta que si cualquiera de los dos diodos se invirtiera, no habría flujo de corriente y todo el potencial de la fuente caería a través del diodo invertido.
Ejemplo\(\PageIndex{4}\)
Determine la corriente de fuente y los voltajes de resistencia para el circuito en la Figura\(\PageIndex{7}\). También encuentre los voltajes de la resistencia si se invierte la polaridad del diodo. Supongamos que la fuente de alimentación es de 10 voltios, el diodo es de silicio y las resistencias son de 1 k\(\Omega\) cada una.
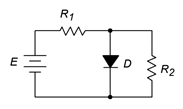
Figura\(\PageIndex{7}\): Esquemática por ejemplo\(\PageIndex{4}\).
Como\(D\) y\(R_2\) están en paralelo deben tener la misma caída de voltaje. Además, el diodo está polarizado hacia adelante. Por lo tanto, el voltaje\(R_2\) transversal debe ser de aproximadamente 0.7 voltios, dejando 9.3 voltios para caer a través\(R_1\). La corriente pasante\(R_1\) es la corriente de origen.
\[I = \frac{E−V_D}{R_1} \nonumber \]
\[I = \frac{10 V−0.7 V}{1k \Omega} \nonumber \]
\[I = 9.3mA \nonumber \]
Si el diodo se invierte se comporta como un interruptor abierto. El circuito se reduce a un simple divisor de voltaje 1:1, cada resistencia cayendo la mitad de la fuente, o 5 voltios cada una.
Simulación por Computadora
Para verificar nuestros resultados, Ejemplo\(\PageIndex{4}\) es simulado. El circuito se captura como se muestra en la Figura\(\PageIndex{8a}\). Este ejemplo en particular se muestra en Multisim aunque cualquier simulador de calidad decente servirá. Aquí se utiliza el diodo de conmutación 1N4148 muy común. Otra opción popular sería el diodo de conmutación 1N914 o un rectificador serie 1N400X.
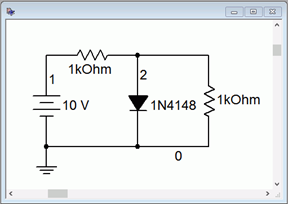
Figura\(\PageIndex{8a}\): El circuito de Ejemplo\(\PageIndex{4}\) en Multisim.
A continuación, se realiza un análisis de punto de funcionamiento de CC. Los resultados se muestran en la Figura\(\PageIndex{8b}\). Tenga en cuenta que el potencial del diodo está justo por debajo de la aproximación de 0.7 voltios. De esto podemos deducir que la caída de voltaje a través de la primera resistencia debe ser ligeramente superior a 9.3 voltios, produciendo una corriente ligeramente superior a 9.3 mA.
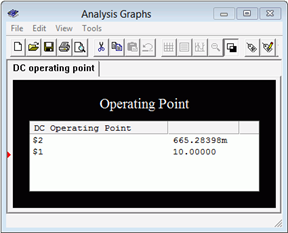
Figura\(\PageIndex{8b}\): Resultados de simulación de punto de funcionamiento de CC para el circuito de Ejemplo\(\PageIndex{4}\).
Finalmente, la Figura\(\PageIndex{8c}\) muestra los resultados cuando el diodo se invierte en el circuito. La segunda resistencia (nodo 3 a tierra) muestra 5 voltios como se esperaba. Por lo tanto, la primera resistencia también debe estar bajando 5 voltios.
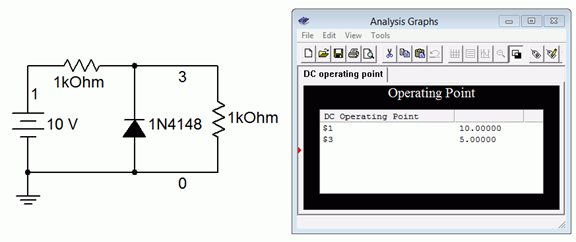
Figura\(\PageIndex{8c}\): Simulación de Ejemplo\(\PageIndex{4}\) usando orientación inversa de diodos.
Antes de pasar a otro tema, echemos un vistazo a un ejemplo algo más involucrado usando múltiples diodos.
Ejemplo\(\PageIndex{5}\)
Determine los voltajes de diodo y resistencia para el circuito en la Figura\(\PageIndex{9}\). Supongamos que los diodos son de silicio.
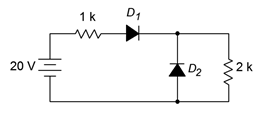
Figura\(\PageIndex{9}\): Esquemática por ejemplo\(\PageIndex{5}\).
Lo primero que hay que notar es que\(D_1\) está sesgado hacia adelante mientras que\(D_2\) es sesgado hacia atrás. Por lo tanto, la fuente de 20 voltios debe igualar la caída transversal\(D_1\) y las dos resistencias. \(D_2\)asumirá lo que sea que la caída a través de los 2 k\(\Omega\) funcione ya que están en paralelo.
\[I = \frac{E−V_{D1}}{R_1+R_2} \nonumber \]
\[I = \frac{20 V−0.7V}{1k\Omega +2 k\Omega} \nonumber \]
\[I = 6.433mA \nonumber \]
Tenga en cuenta que prácticamente ninguna corriente fluye hacia abajo,\(D_2\) ya que es de polarización inversa. Usando la ley de Ohm, la caída a través de la primera resistencia es de 6.433 voltios y para la segunda resistencia, 12.867 voltios.
Referencias
1 La gráfica I-V no es una línea recta (lineal) y los cuadrantes delantero e inverso no son idénticos (bilaterales).
2 La resistencia dinámica de una unión PN puede aproximarse a 26 mV/\(I_{junction}\). Esto se mostrará en un próximo capítulo.


