4.3: Curvas de colector BJT

Una de las gráficas de dispositivos BJT más útiles es la familia de curvas colectoras. Se trata de una serie de gráficas de corriente de colector\(I_C\), versus voltaje colector-emisor\(V_{CE}\), en diferentes niveles de corriente base,\(I_B\). Para generar estas curvas conducimos el terminal base con una fuente de corriente fija estableciendo\(I_B\). Una fuente de alimentación de CC se conecta desde el colector al emisor y luego se barre de cero voltios a algún valor superior. Esto establece\(V_{CE}\). Simultáneamente, rastreamos la corriente de colector resultante y trazamos el resultado. Esto da como resultado una traza. Luego se aumenta la corriente base y el suministro de CC se vuelve a barrer para una segunda traza. Este proceso se repite para crear una familia de curvas. Un ejemplo se muestra en la Figura\(\PageIndex{1}\).

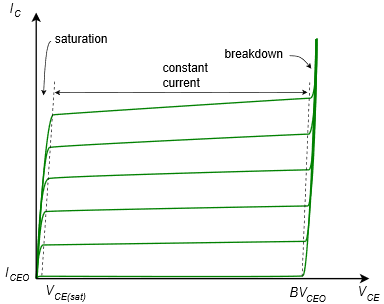
Figura\(\PageIndex{1}\): Una familia de curvas colectoras.

Los resultados de la curva inferior cuando\(I_B = 0\). Idealmente, la corriente de colector correspondiente sería 0 pero se produce una pequeña corriente de fuga. Esto generalmente se conoce como\(I_{CEO}\), es decir, la corriente\(C\)\(E\) ollector-mitter con la\(O\) pluma terminal base (es decir, sin corriente base). Las curvas por encima de esta corresponden a niveles crecientes de corriente base; cada nueva corriente base aumenta una cantidad fija para cada traza posterior (por ejemplo, 0\(\mu\) A, 10\(\mu\) A, 20\(\mu\) A, 30\(\mu\) A, etc.).

Lo más llamativo de este conjunto de curvas es que existen tres regiones o zonas de operación distintas. Al extremo izquierdo de la curva la corriente se eleva rápidamente. A esto se le conoce como la región de saturación. El punto de ruptura es bastante pequeño con solo unas décimas de voltio. Esto se puede encontrar en una hoja de datos como\(V_{CE(sat)}\). La región de saturación se utiliza en aplicaciones de conmutación de transistores.

En el extremo derecho se encuentra otra región donde la corriente colectora se eleva rápidamente. A esto se le llama la región de desglose. Este es el mismo efecto que vimos con diodos individuales. No deseamos operar dispositivos en esta región ya que pueden resultar daños. El voltaje de ruptura se denota en la mayoría de las hojas de datos como\(BV_{CEO}\) (\(C\)ollector a\(E\) mitter voltaje con una base de\(O\) pluma). Para los dispositivos de propósito general esto estará en el rango de 30 a 60 voltios más o menos, pero puede ser mucho mayor.

Entre estos dos extremos se encuentra una región donde la corriente del colector es relativamente constante, mostrando sólo una modesta pendiente positiva. Esta es la región de corriente constante. Aquí es donde queremos que opere el transistor para aplicaciones como amplificadores lineales.

Un dispositivo llamado trazador de curvas se puede utilizar para generar esta familia de curvas en el laboratorio. Una muy buena aproximación para se\(\beta\) puede determinar usando estas curvas. Primero, determinamos los valores aproximados del circuito para\(I_C\) y\(V_{CE}\), y ubicamos este punto en la gráfica. Luego encontramos la línea de trama más cercana a ese punto. Desde la intersección de\(V_{CE}\) y y esta línea de trazado, rastreamos de regreso al eje vertical para encontrar el valor preciso de\(I_C\) para esa traza. Contamos el número de trazas y multiplicamos por el tamaño de paso actual base para determinar la corriente base correspondiente. Luego dividimos los dos valores y llegamos a\(\beta\).

Ejemplo\(\PageIndex{1}\)

Supongamos que tenemos un BJT operando a\(V_{CE} = 30\) V y\(I_C = 4\) mA. Si el dispositivo se coloca en un trazador de curvas y la familia resultante de curvas aparece como en la Figura\(\PageIndex{2}\), determine el valor de\(\beta\). Supongamos que la corriente base se incrementa 10\(\mu\) A por traza.

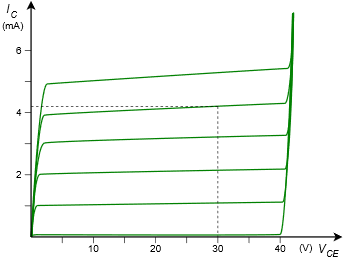
Figura\(\PageIndex{2}\): Visualización del trazador de curvas para Ejemplo\(\PageIndex{1}\).

Primero, encuentra un rastro cerca del punto de operación de 30 voltios y 4 mA. Dibuje una línea vertical a 30 voltios y deténgase cuando esa línea intersecta la traza más cercana a 4 mA. En este ejemplo ese es el segundo rastro desde arriba. Desde ese punto de intersección, realice un seguimiento de regreso al eje vertical para determinar la corriente precisa del colector. Eso es aproximadamente 4.2 mA aquí. Para determinar la corriente base, cuente hasta el número de trazas a la traza seleccionada. La traza seleccionada es la cuarta hacia arriba (no incluya la traza inferior donde\(I_B\) está 0). La corriente base se incrementa en 10\(\mu\) A por rastro de manera que nos deja con\(I_B = 40\)\(\mu\) A.

\[\beta = \frac{I_C}{I_B} \nonumber \]

\[\beta = \frac{4.2 mA}{40\mu A} \nonumber \]

\[\beta = 105 \nonumber \]

4.3.1: Aumento\(\beta\) y Tensión Temprana

Al mirar las curvas del colector, una buena pregunta que podríamos hacernos es por qué la corriente del colector aumenta a medida que\(V_{CE}\) aumenta. Esto se debe al hecho de que el aumento del voltaje colector-emisor es responsable de un aumento en el voltaje colector-base (por definición,\(V_{CE} = V_{CB} + V_{BE}\)). \(V_{CB}\)es el potencial de polarización inversa en la unión PN colector-base. A medida que aumenta este potencial inverso, la región de agotamiento de la base colectora se ensancha. A medida que se ensancha, penetra más en la capa base. Debido a que la base se estrecha efectivamente, las posibilidades de recombinación se reducen, reduciendo así la corriente de base y aumentando efectivamente\(\beta\).

Si extendemos las trazas de la región de corriente constante de nuevo en el segundo cuadrante, se cruzan en un punto llamado Voltaje Temprano, llamado así por James Early, y denotado como\(V_A\). Esto se ilustra en la Figura\(\PageIndex{3}\).

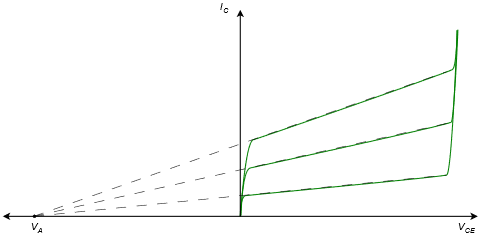
Figura\(\PageIndex{3}\): Voltaje Temprano.