4.5: Modelo Ebers-Moll

Un buen modelo funcional del BJT es el modelo simplificado de Ebers-Moll que se muestra en la Figura\(\PageIndex{1}\). Esto utiliza un diodo ideal para modelar la unión base-emisor y una fuente de corriente controlada por corriente ubicada en el colector-base. Este modelo es suficiente para lograr buenos resultados de análisis con una variedad de circuitos de CC y baja frecuencia. Es importante recordar, sin embargo, que\(\beta\) varía no solo de un dispositivo a otro, sino que también varía con los cambios de temperatura, corriente de colector y voltaje colector-emisor.

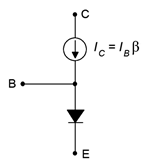
Figura\(\PageIndex{1}\): Modelo Ebers-Moll del BJT NPN.

Podemos usar el modelo Ebers-Moll en circuitos básicos de polarización de CC. Para sesgar correctamente el BJT necesitamos hacer que la base colector-base sea polarizada inversa y la base-emisor sesgada hacia adelante. En otras palabras,\(V_C > V_B > V_E\). Hay muchas maneras de lograrlo. Un método coloca el emisor a tierra, una fuente de CC modesta en el bucle base-emisor y una fuente de CC algo más alta en el colector. Un ejemplo se muestra en la Figura\(\PageIndex{2}\).

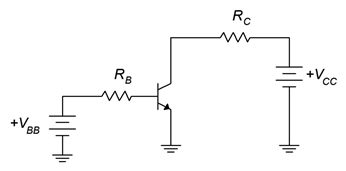
Figura\(\PageIndex{2}\): Circuito de polarización de base simple.

Las dos resistencias sirven para limitar las corrientes y tensiones del transistor. Debido a que el emisor está en tierra, el punto común, este circuito se clasifica como teniendo una configuración de emisor común. Hay muchos circuitos emisores comunes posibles. Nos referiremos a éste específicamente como sesgo de base.

Ahora, reemplacemos el transistor con el modelo Ebers-Moll. El resultado, con polaridades de voltaje agregado y direcciones de corriente, se muestra en la Figura\(\PageIndex{3}\).

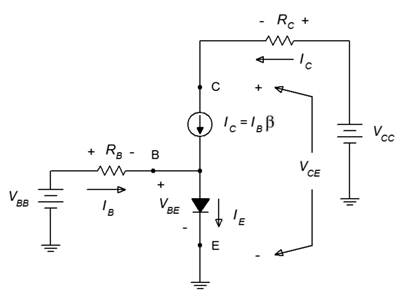
Figura\(\PageIndex{3}\): Circuito de polarización base con modelo EbersMoll.

Los valores dados para las resistencias, fuentes de alimentación y\(\beta\), todas las corrientes y voltajes se pueden determinar utilizando técnicas fundamentales de análisis de circuitos. La idea básica es crear ecuaciones KVL para los dos bucles y luego expandirlas usando la ley de Ohm. Comenzamos con el bucle base-emisor.

\[V_{BB} = V_{R_B} +V_{BE} \\ V_{BB} = I_B R_B+V_{BE} \\ I_B = \frac{V_{BB} - V_{BE}}{R_B} \label{4.3} \]

Y para el bucle colector-emisor:

\[V_{CC} = V_{R_C} +V_{CE} \\ V_{CC} = I_C R_C + V_{CE} \\ V_{CE} = V_{CC} − I_C R_C \label{4.4} \]

Para obtener\(I_C\), recordemos eso\(I_C = \beta I_B\).

Ejemplo\(\PageIndex{1}\)

Determinar las corrientes circulantes y los voltajes del dispositivo para el circuito de la Figura\(\PageIndex{2}\) si\(V_{BB} = 10\)\(V_{CC} = 15\) V, V\(\Omega\),\(R_B = 200\) k,\(R_C = 1\) k\(\Omega\) y\(\beta\) = 100. Supongamos que el transistor es de silicio.

Primero, encuentra la corriente base. KVL dicta que el voltaje transversal\(R_B\) es de 9.3 voltios.

\[I_B = \frac{V_{BB} −V_{BE}}{R_B} \nonumber \]

\[I_B = \frac{10 V −0.7V}{200 k\Omega} \nonumber \]

\[I_B = 46.5\mu A \nonumber \]

Ahora encuentra la corriente de colector y sigue con la ley de Ohm y KVL.

\[I_C = \beta I_B \nonumber \]

\[I_C = 100\times 46.5\mu A \nonumber \]

\[I_C = 4.65mA \nonumber \]

\[V_{CE} = V_{CC} −I_C R_C \nonumber \]

\[V_{CE} = 15V −4.65 mA\times 1k\Omega \nonumber \]

\[V_{CE} = 10.35 V \nonumber \]

En aras de la integridad, el voltaje transversal\(R_C\) es de 4.65 voltios,\(V_{CB}\) es de 9.65 voltios y\(I_E\) es de 4.6965 mA.

El ejemplo anterior ilustra que el lugar para iniciar el análisis está en el bucle baseemisor en lugar del bucle colector-emisor. Esto se debe a que en el bucle base-emisor tenemos la unión base-emisor polarizada hacia delante que tiene un potencial conocido (aproximadamente 0.7 voltios). Por el contrario, la tensión colector-emisor es desconocida, ya que incluye la unión colector-base polarizada inversa. Ese voltaje dependerá de otros elementos del circuito, más notablemente la resistencia del colector y la fuente asociada.

Una mejora en el circuito de Ejemplo\(\PageIndex{1}\) sería rediseñarlo para una sola fuente de alimentación en lugar de dos fuentes. Esto es fácil de hacer. Todo lo que se necesita es mantener la corriente base sin cambios. Si eso permanece en su valor original, entonces la corriente del colector no cambiará y, en consecuencia, tampoco cambiará nada en el bucle colector-emisor. El uso de la fuente de 15 voltios\(V_{BB}\) significa que el voltaje\(R_B\) transversal aumentará a 14.3 voltios. La ley de Ohm indica entonces que\(R_B\) deben ser 14.3 voltios divididos entre 46.5\(\mu\) A, o 307.5 k\(\Omega\).

4.5.1: Problemas de\(\beta\) variación

Existe un problema importante con el circuito de la Figura\(\PageIndex{2}\), a saber, carece de estabilidad de corriente de colector y voltaje colector-emisor. Como veremos en los próximos capítulos, es importante mantener estos parámetros estables para asegurar un rendimiento consistente para muchos tipos de circuitos. Como señalamos en nuestra inspección de la hoja de datos 2N3904, la variación de\(\beta\) puede ser bastante grande en un punto de operación dado. Si además sumamos la varianza debido a la temperatura y otros factores, podemos estar viendo un rango de 10:1. Si repetimos Ejemplo\(\PageIndex{1}\) con un duplicado\(\beta\) de 200, el bucle base-emisor no cambia pero la corriente del colector se duplica a 9.3 mA. Esto aumenta la caída de voltaje\(R_C\) a través de 9.3 voltios que luego obliga\(V_{CE}\) a caer a 5.7 voltios. Dado un ciclo de producción típico de transistores, este circuito podría exhibir corrientes de colector de menos de 4 mA a más de 10 mA. En algunas aplicaciones esta variación en la corriente podría ser tolerable pero no en todas ellas. Por ejemplo, supongamos que un LED se coloca en serie con\(R_C\). Debido a que el brillo de un LED depende de su nivel actual, el brillo ahora dependerá del\(\beta\) del BJT específico utilizado. Si se trata de un LED en una pantalla más grande compuesta por circuitos similares, entonces la iluminación será desigual entre ellos haciendo que toda la pantalla aparezca apagada.

De hecho, si este circuito fue construido en el laboratorio, es muy probable que después de encender la alimentación, se podría ver subir\(I_C\) lentamente en su amperímetro. Esto se debe a que el BJT comenzará a calentarse a medida que disipa la energía. Como se señala en la hoja de datos,\(\beta\) aumenta con el aumento de la temperatura. Porque\(I_B\) es un valor fijo, cualquier subida de\(\beta\) medios que también\(I_C\) debe subir. Este aumento de la corriente tenderá a causar un aumento adicional en la disipación de potencia y la temperatura, lo que provoca un aumento adicional en\(\beta\), y los ciclos del proceso. Hemos creado un bucle de retroalimentación térmica positiva inadvertida. Si no se controlan, los dispositivos podrían sobrecalentarse y ser destruidos. Examinaremos los circuitos de polarización que logren una alta estabilidad en el próximo capítulo.

Hay otro aspecto interesante en este circuito. Como se señaló, si sustituyéramos el BJT original por otra unidad que tuviera una mayor\(\beta\), la corriente del colector subiría. ¿Y si continuamos esto a\(\beta\) valores cada vez más altos? Por ejemplo, si aumentáramos\(\beta\) a 400 (es cierto, bastante alta) la nueva corriente de colector parecería saltar hasta 46.5\(\mu\) A\(\cdot\) 400, o 18.6 mA. Hay un problema “pequeño” con este valor. La ley de Ohm indica que esta corriente desarrollaría una caída de 18.6 voltios a través del 1 k\(\Omega\)\(R_C\) pero eso es imposible porque\(V_{CC}\) es de solo 15 voltios. La única forma en que “funciona” es si de alguna manera el BJT se transforma mágicamente en una batería de 3.6 voltios. Ninguna cantidad de oración o cartas a Santa hará que eso suceda ¹.

Referencias

¹ Ambos siendo igualmente efectivos.