4.6: Líneas de carga de CC

Última actualización
Guardar como PDF

Page ID: 83450

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Entonces, ¿cómo determinamos el rango de posibles valores de corriente de colector y voltaje colector-emisor en cualquier circuito de CC BJT dado? Una respuesta es emplear el concepto de la línea de carga de CC. En general, una línea de carga es una gráfica de todos los pares de coordenadas posibles de\(I_C\) y\(V_{CE}\) para un transistor en un circuito dado. Refiriéndose de nuevo a la Figura 4.5.3, recogemos con la Ecuación 4.5.2 y la resolvemos para\(I_C\):

\[V_{CE} = V_{CC} −I_C R_C \\ I_C = \frac{1}{R_C} (V_{CC} −V_{CE} ) \\ I_C = − \frac{1}{R_C} V_{CE} + \frac{V_{CC}}{R_C} \label{4.5} \]

La ecuación\ ref {4.5} es una ecuación lineal de la forma\(y = mx + b\). La intercepción y (el valor de\(I_C\) cuándo\(V_{CE} = 0\)) es\(V_{CC}/R_C\). Esta es la corriente de colector máxima que se puede lograr. En este punto el transistor está saturado y este máximo se conoce como\(I_{C(sat)}\). La intercepción x (el valor de\(V_{CE}\) cuándo\(I_C = 0\)) es\(V_{CC}\). Esto representa el mayor voltaje posible a través del colector-emisor del transistor. En este punto se corta la corriente, y por lo tanto se llama a este voltaje\(V_{CE(cutoff)}\). Por último, la pendiente de la línea es\(−1/R_C\). Se muestra una gráfica en la Figura\(\PageIndex{1}\).

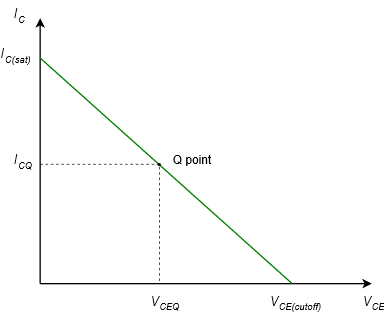
Figura\(\PageIndex{1}\): Línea genérica de carga CC.

Para completar la gráfica, también incluimos el punto de operación para algún transistor específico. Esto se llama punto quiescente, o punto Q, y la corriente y voltaje del dispositivo asociado se llaman\(I_{CQ}\) y\(V_{CEQ}\). Todos los puntos Q posibles yacen en esta línea.

Volviendo al Ejemplo 4.5.1 y usando la Ecuación\ ref {4.5}, podemos resumir el circuito de la siguiente manera:

\[I_{C(sat)} = 15 mA \\ V_{CE(cutoff)} = 15 V \nonumber \]

\[\text{Q Point for } \beta = 100: \\ I_C = 4.65 mA \\ V_{CE} = 10.35 V \nonumber \]

\[\text{Q Point for } \beta = 200: \\ I_C = 9.3 mA \\ V_{CE} = 5.7 V \nonumber \]

Esto se representa en la Figura\(\PageIndex{2}\).

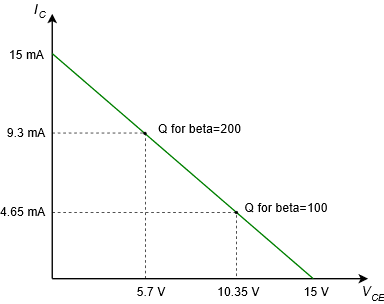
Figura\(\PageIndex{2}\): Línea de carga para las variaciones del Ejemplo 4.5.1.

Si calculamos una corriente de colector que es mayor que la corriente de saturación, entonces sabemos que la corriente real será la corriente máxima de saturación. Para este circuito, cualquier valor calculado mayor a 15 mA indica que el transistor produciría solo 15 mA (nuestro ejemplo anterior usando\(\beta\) = 400, por ejemplo). En realidad, el verdadero valor será muy ligeramente menor. Esto se debe a que el voltaje colector-emisor no baja hasta cero voltios cuando el dispositivo está saturado. Por lo general,\(V_{CE(sat)}\) será una décima parte de un voltio más o menos para dispositivos de señal pequeños. Los valores precisos se pueden determinar a partir de gráficas de dispositivos como la gráfica media de la Figura 4.4.1c, etiquetada como “Región de Saturación del Colector”. A modo de ejemplo, si\(I_C\) = 10 mA y\(I_B\) = 0.3 mA, entonces\(V_{CE(SAT)}\) es aproximadamente 0.15 V. Resulta que podemos utilizar la saturación a nuestra ventaja en la conmutación de circuitos, como estamos a punto de ver.