5.3: Bias del emisor de dos fuentes

Para un correcto funcionamiento, la unión colector-base debe estar polarizada hacia atrás y la unión base-emisor debe estar polarizada hacia adelante. Para un transistor NPN eso significa que el colector debe estar en el potencial más alto, la base algo más baja y el emisor en el potencial más bajo de los tres. Una forma de hacerlo es aplicar el suministro positivo habitual al colector, pero en lugar de usar un segundo potencial en la base, la base está atada a tierra a través de una resistencia. La polarización directa requerida en el emisor base se logra entonces conectando el emisor a una fuente de alimentación negativa. Esta configuración de circuito se muestra en la Figura\(\PageIndex{1}\) usando un dispositivo NPN. Nos referiremos a esto como polarización del emisor de dos fuentes.

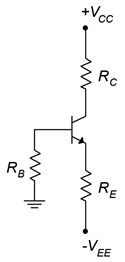
Figura\(\PageIndex{1}\): Bialización de emisor de dos fuentes, versión NPN.

Podemos derivar una ecuación para la corriente del colector aplicando KVL al bucle baseemitter:

\[V_{EE} = V_{R_B} +V_{BE}+V_{R_E} \nonumber \]

\[V_{EE} = I_B R_B+V_{BE}+I_E R_E \nonumber \]

Recordando eso\(I_B = I_C/ \beta\) y\(I_E \approx I_C\),

\[V_{EE} = (I_C/ \beta )R_B+V_BE+ I_C R_E \nonumber \]

Resolviendo para\(I_C\) que lleguemos a

\[I_C = \frac{∣V_{EE}∣−V_{BE}}{R_E+R_B / \beta} \label{5.1} \]

El valor absoluto se ha agregado a la tensión de alimentación del emisor por lo que no hay confusión con respecto al signo de este potencial en la ecuación.

Lo que hay que notar sobre la Ecuación\ ref {5.1} es que\( \beta \) solo determina parcialmente la corriente del colector. De hecho, si podemos hacer\(R_E \gg R_B/ \beta\), entonces la ecuación se reduce a

\[I_C \approx \frac{∣V_{EE}∣−V_{BE}}{R_E} \label{5.2} \]

Es relativamente fácil lograr la\(R_E \gg R_B/ \beta\) estipulación. Dados los valores típicos de\( \beta \), este será el caso si\(R_E\) es aproximadamente igual o mayor que\(R_B\). Lo que encontramos en esta instancia es que casi todo el suministro del emisor cae\(R_E\) a través para establecer un establo\(I_C\) con prácticamente ningún papel\( \beta \) jugando. Si\( \beta \) cambia, el resultado será un cambio inverso en\(I_C\) permaneciendo en\(I_B\) gran medida sin cambios.

Ahora que tenemos la corriente del colector, cualquier otra corriente o voltaje en el circuito puede derivarse aplicando la ley de Ohm, KVL y similares. Por ejemplo, para encontrar\(V_C\), el voltaje del colector a tierra,

\[V_C = V_{CC} − V_{R_C} \nonumber \]

\[V_C = V_{CC} − I_C R_C \nonumber \]

Y para encontrar el voltaje colector-emisor del transistor,\(V_{CE}\),

\[V_{CE} = V_{CC}+∣V_{EE}∣−V_{RC} −V_{RE} \\ V_{CE} = V_{CC}+∣V_{EE}∣−I_C R_C −I_C R_E \\ V_{CE} = V_{CC}+∣V_{EE}∣−I_C (R_C+R_E ) \label{5.3} \]

Tenga en cuenta que también se\(V_{CE}\) puede encontrar a través de\(V_{CE} = V_C − V_E\). Voltajes de caída a lo largo de los rendimientos del bucle base-emisor

\[V_E = −V_{R_B} −V_{BE} \nonumber \]

\[V_E = −I_B R_B −V_{BE} \nonumber \]

Además, es para nuestra ventaja desarrollar la línea de carga de CC para esta configuración. La línea de carga puede servir como una “comprobación de cordura” para nuestros cálculos. Para encontrar los puntos finales,\(I_{C(sat)}\) es la corriente máxima y ocurrirá cuando\(V_{CE} = 0\). Si imaginamos que la corriente sube como\(V_{CE}\) colapsa, eventualmente todo el voltaje de suministro disponible habrá caído a través de\(R_C\) y\(R_E\). Así

\[I_{C(sat)} = \frac{V_{CC}+∣V_{EE}∣}{R_C+R_E} \label{5.4} \]

De igual manera,\(V_{CE(cutoff)}\) ocurre cuando\(I_C = 0\). Eso significa que no habrá potenciales a través\(R_C\) y\(R_E\). Por lo tanto,\(V_{CE}\) “absorbe” todo el voltaje de fuente disponible.

\[V_{CE (cutoff )} = V_{CC}+∣V_{EE} ∣ \label{5.5} \]

No intente memorizar todas las innumerables ecuaciones presentadas. Simplemente hay demasiadas variaciones sobre el tema y solo empeorará cuando se introduzcan otras configuraciones de sesgo. En su lugar, recuerde cómo encontrar la corriente de colector y luego adquirir el hábito de aplicar la ley de Ohm y KVL para derivar cualquier otra cosa que pueda necesitar.

En este punto se pide un ejemplo integral.

Ejemplo\(\PageIndex{1}\)

Suponiendo\( \beta = 100\), trazar el punto Q (\(I_C\)y\(V_{CE}\)) en la línea de carga para el circuito de la Figura\(\PageIndex{2}\).

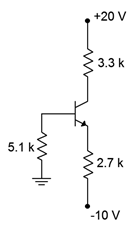
Figura\(\PageIndex{2}\): Circuito por Ejemplo\(\PageIndex{1}\).

Usando la ecuación\ ref {5.1}:

\[I_C = \frac{∣V_{EE} ∣−V_{BE}}{R_E+R_B / \beta} \nonumber \]

\[I_C = \frac{10 −0.7}{2.7k \Omega +5.1 k \Omega /100} \nonumber \]

\[I_C = 3.38 mA \nonumber \]

Observando los tamaños relativos de\(R_E\) y\(R_B\), la aproximación debe ser cercana.

\[I_C = \frac{∣V_{EE} ∣−V_{BE}}{R_E} \nonumber \]

\[I_C = \frac{10 −0.7}{2.7 k \Omega} \nonumber \]

\[I_C = 3.44 mA \nonumber \]

Para encontrar\(V_{CE}\) podemos usar la ecuación derivada anteriormente (Ecuación\ ref {5.3}).

\[V_{CE} = V_{CC} +∣V_{EE}∣− I_C(R_C+R_E ) \nonumber \]

\[V_{CE} = 20 V+10 V −3.38mA(3.3 k \Omega +2.7k \Omega ) \nonumber \]

\[V_{CE} = 9.72 V \nonumber \]

Ahora calcule los puntos finales de la línea de carga:

\[I_{C(sat)} = \frac{V_{CC}+∣V_{EE} ∣}{R_C+R_E} \nonumber \]

\[I_{C(sat)} = \frac{20 V+10V}{3.3K \Omega +2.7K \Omega} \nonumber \]

\[I_{C(sat)} = 5 mA \nonumber \]

\[V_{CE (cutoff )} = V_{CC} +∣V_{EE}∣ \nonumber \]

\[V_{CE (cutoff )} = 20 V+−10 V \nonumber \]

\[V_{CE (cutoff )} = 30 V \nonumber \]

La línea de carga para el circuito en Ejemplo\(\PageIndex{1}\) se muestra en la Figura\(\PageIndex{3}\).

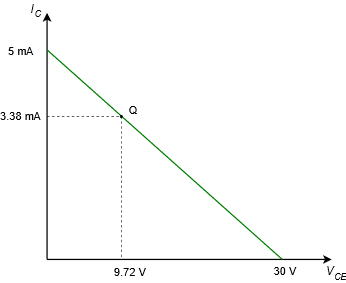
Figura\(\PageIndex{3}\): Línea de carga de CC para el circuito de la Figura\(\PageIndex{2}\).

Anote las proporciones entre voltaje y corriente para el punto Q. El voltaje es un poco menos de un tercio del máximo mientras que la corriente es un poco más de dos tercios de su máximo.

5.3.1: Verificación de Estabilidad

Se hizo la afirmación de que los circuitos de polarización de emisor de dos fuentes como el de la Figura\(\PageIndex{1}\) potencialmente tienen un punto Q estable. Si tuviéramos que trazar un segundo punto Q para un gran cambio en\( \beta \), difícilmente debería moverse, indicando así una estabilidad muy alta. Por ejemplo, duplicar\( \beta \) a 200 da como resultado\(I_C = 3.41\) mA y\(V_{CE} = 9.53\) V. El nuevo punto Q se ha acercado un poco más a la saturación, produciendo alrededor de un 1% de cambio en la corriente para un cambio del 100% en\( \beta \). Claramente, esta configuración puede producir cambios muy pequeños en el punto Q a pesar de cambios muy grandes en\( \beta \).

5.3.2: Simulación por Computadora

El circuito de polarización del emisor de dos fuentes de la Figura\(\PageIndex{4}\) se simula utilizando la función de polarización de CC. Una estimación rápida muestra que esperamos alrededor de 2 mA de corriente de colector (9.3 V/4.7 k\( \Omega \)) y un voltaje de colector de aproximadamente 8 voltios (15 V − 2 mA\(\cdot\) 3.6 k\( \Omega \)). También esperamos un pequeño potencial negativo en la base\(−I_BR_B\)). \( \beta \)Dados los valores típicos para el 2N3904 (200-ish a esta corriente, refiérase de nuevo a la hoja de datos), esperamos una corriente base de alrededor de 10 a 15\(\mu\) A, dejándonos con una\(V_B\) de aproximadamente −0.1 voltios. El voltaje del emisor sería aproximadamente 0.7 voltios menos que eso, quizás −0.8 voltios más o menos.

En definitiva, para un circuito debidamente diseñado de este tipo esperamos\(V_B\) estar bastante cerca de 0 V y\(V_E\) que sea de aproximadamente −0.7 voltios.

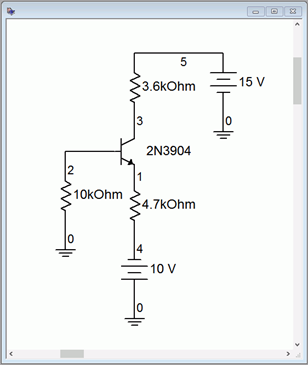
Figura\(\PageIndex{4}\): Esquema para simulación de polarización de emisor de dos fuentes.

Los resultados se muestran en la Figura\(\PageIndex{5}\). Los voltajes de los nodos concuerdan con nuestras estimaciones. El Nodo 3 es el voltaje del colector, muy cerca de la estimación. Los resultados para la tensión base (nodo 2) y la tensión del emisor (nodo 1) también están en línea con las estimaciones.

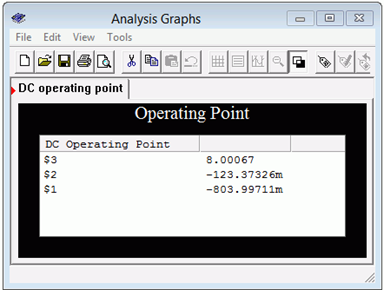
Figura\(\PageIndex{5}\): Resultados de simulación para circuito de polarización de emisor de dos fuentes.

5.3.3: Polarización del emisor de dos fuentes PNP

Si bien es posible crear una versión PNP de circuitos de polarización simplemente intercambiando el dispositivo y luego cambiando los signos de las fuentes de alimentación, es común “voltear” todo el circuito de arriba a abajo para que el emisor se enrolla en la parte superior y el colector en la parte inferior. Una ventaja de esto es que, en un esquema de circuito multitransistor, todas las corrientes de polarización de CC “corren por la página”, es decir, las corrientes de colector fluyen desde la parte superior de la página hasta la parte inferior de la página. La figura\(\PageIndex{6}\) muestra un circuito de polarización de emisor de dos fuentes PNP.

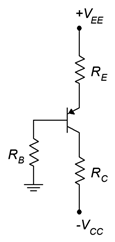
Figura\(\PageIndex{6}\): Circuito de polarización del emisor de dos fuentes PNP.

Todas las ecuaciones de corriente del dispositivo y las ecuaciones de voltaje de componentes derivadas para la versión NPN se mantendrán para la versión PNP. Las diferencias a recordar son que las polaridades de voltaje se invertirán (lo que fue positivo en el NPN es negativo en el PNP) y las direcciones de corriente se invertirán (por ejemplo, la corriente convencional fluye hacia el colector del NPN pero fuera del colector del PNP. Por ejemplo, en el NPN esperamos que la corriente base fluya hacia el terminal base. Esto crea un pequeño voltaje negativo en la base y un voltaje algo más negativo (por 0.7 V) en el emisor. En el PNP, la corriente base fluye fuera de la base. Esto crea un pequeño voltaje positivo en la base y da como resultado que el emisor sea ligeramente más positivo (en 0.7 V). Esto quizás se ilustra mejor con un ejemplo.

Ejemplo\(\PageIndex{2}\)

Suponiendo\( \beta = 100\), determinar el punto Q y los puntos finales de la línea de carga del circuito de la Figura\(\PageIndex{7}\).

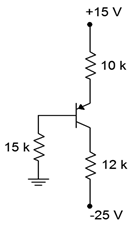
Figura\(\PageIndex{7}\): Circuito por Ejemplo\(\PageIndex{2}\).

Primero, tenga en cuenta que se trata de un PNP dibujado al revés por lo que el emisor está en la parte superior. Usando la ecuación\ ref {5.1}:

\[I_C = \frac{∣V_{EE}∣−V_{BE}}{R_E+R_B / \beta} \nonumber \]

\[I_C = \frac{15−0.7}{10 k \Omega +15k \Omega /100} \nonumber \]

\[I_C = 1.409mA \nonumber \]

Como verificación cruzada, señalando los tamaños relativos de\(R_E\) y\(R_B\), la aproximación debe ser cercana.

\[I_C = \frac{∣V_{EE}∣−V_{BE}}{R_E} \nonumber \]

\[I_C = \frac{15 −0.7}{10 k \Omega} \nonumber \]

\[I_C = 1.43 mA \nonumber \]

Para encontrar\(V_{CE}\) podemos usar la Ecuación\ ref {5.3} con una ligera modificación.

\[V_{CE} = V_{EE} + ∣V_{CC}∣−I_C (R_C+R_E ) \nonumber \]

\[V_{CE} = 15V+25 V −1.409mA(12 k \Omega +10k \Omega ) \nonumber \]

\[V_{CE} = 9V \nonumber \]

Completamos la imagen determinando los puntos finales de la línea de carga.

\[I_{C(sat)} = \frac{V_{EE} + ∣V_{CC}∣}{R_C+R_E} \nonumber \]

\[I_{C(sat)} = \frac{10 V+25V}{12 K \Omega +10 K \Omega} \nonumber \]

\[I_{C(sat)} = 1.818mA \nonumber \]

\[V_{CE (cutoff )} = V_{EE}+∣V_{CC}∣ \nonumber \]

\[V_{CE (cutoff )} = 15 V+25 V \nonumber \]

\[V_{CE (cutoff )} = 40 V \nonumber \]

El punto Q es aproximadamente 3/4 de la corriente máxima y 1/4 de la tensión máxima.