5.4: Bias del divisor de voltaje

Otra configuración que puede proporcionar una alta estabilidad de polarización es la polarización del divisor de voltaje. En lugar de usar una fuente negativa fuera de la resistencia del emisor, como la polarización del emisor de dos fuentes, esta configuración devuelve la resistencia del emisor a tierra y eleva la tensión base. Para evitar problemas con una segunda fuente de alimentación, esta tensión base se deriva de la fuente de alimentación del colector a través de un divisor de voltaje. La plantilla de sesgo se muestra en la Figura\(\PageIndex{1}\).

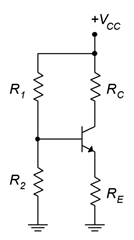
Figura\(\PageIndex{1}\): Polarización del divisor de voltaje.

Derivamos las ecuaciones para la línea de carga. Primero, consideremos los puntos finales de saturación y corte. Para la saturación, asuma\(V_{CE}\) va a 0. ¿Qué resistencias quedan para limitar la corriente?

\[I_{C(sat)} = \frac{V_{CC}}{R_C+R_E} \label{5.6} \]

\(V_{CE(cutoff)}\)ocurre cuando\(I_C = 0\) y eso significa que no habrá potenciales a través\(R_C\) y\(R_E\). Por lo tanto,\(V_{CE}\) toma todo el voltaje de fuente disponible.

\[V_{CE (cutoff )} = V_{CC} \label{5.7} \]

La clave para encontrar el punto Q (y prácticamente cualquier otra corriente o voltaje en el circuito) es encontrar\(I_C\). Para simplificar el proceso, Thevenize el divisor de voltaje como se muestra en la Figura\(\PageIndex{2}\).

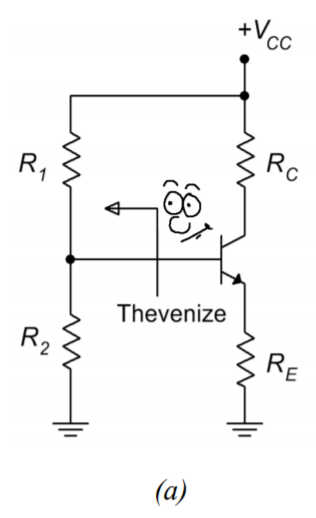
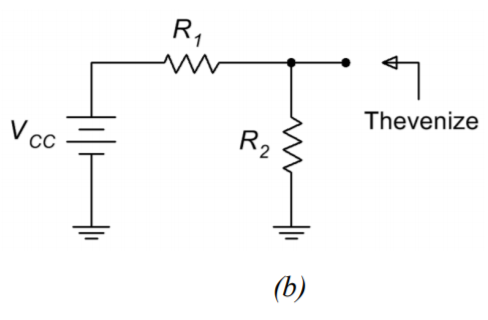
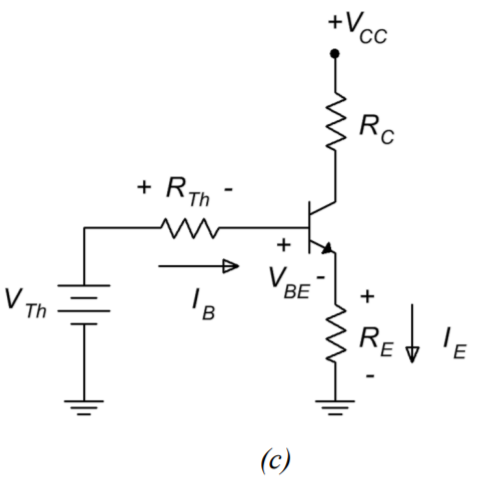
Figura\(\PageIndex{2}\): La evenización del divisor de voltaje.

Por inspección de la Figura\(\PageIndex{2b}\),

\[V_{TH} = V_{CC} \frac{R_2}{R_1+R_2} \nonumber \]

\[R_{TH} = R_1 || R_2 = \frac{R_1 R_2}{R_1+R_2} \nonumber \]

Ahora podemos derivar una ecuación para la corriente del colector aplicando KVL al bucle base-emisor de la Figura\(\PageIndex{2c}\):

\[V_{TH} = V_{R_{TH}} +V_{BE}+V_{R_E} \nonumber \]

\[V_{TH} = I_B R_{TH} + V_{BE} + I_E R_E \nonumber \]

Recordando eso\(I_B = I_C/ \beta \) y\(I_E \approx I_C\),

\[V_{TH} = (I_C / \beta )R_{TH} + V_{BE}+I_C R_E \nonumber \]

Resolviendo para\(I_C\) que lleguemos a

\[I_C = \frac{V_{TH} − V_{BE}}{R_E+R_{TH} / \beta} \label{5.8} \]

¿Podemos encontrar una aproximación rápida para\(I_C\) también? Si asumimos que el divisor de voltaje de\(R_1\) y\(R_2\) está ligeramente cargado, es decir, que la corriente del divisor es mucho, mucho menor que la corriente base, encontrar\(I_C\) es fácil. El voltaje del divisor produce el voltaje base. Luego restamos la caída de 0.7 voltios en el base-emisor y lo que queda cae a través\(R_E\). A partir de ahí es una aplicación corta de la ley de Ohm para obtener\(I_E\), que es aproximadamente igual a\(I_C\). Pero, ¿cómo sabemos si el divisor está ligeramente cargado en primer lugar sin pasar por el equivalente Thevenin? Mirando la Ecuación\ ref {5.8}, siempre y cuando\(R_E \gg R_{TH}/ \beta \), podamos ignorar el segundo término en el denominador, dejándonos con nuestra rápida aproximación. Dados los valores típicos para\( \beta \), siempre y cuando no\(R_2\) sea mucho mayor que\(R_E\), la aproximación será razonablemente precisa.

Una vez\(I_C\) obtenido podemos encontrar la tensión colector-emisor del transistor\(V_{CE}\),

\[V_{CE} = V_{CC} −V_{R_C} −V_{R_E} \\ V_{CE} = V_{CC} −I_C R_C −I_C R_E \\ V_{CE} = V_{CC} −I_C (R_C+R_E ) \label{5.9} \]

Es hora de otro ejemplo ilustrativo emocionante.

Ejemplo\(\PageIndex{1}\)

Suponiendo\( \beta = 200\), trazar el punto Q (\(I_C\)y\(V_{CE}\)) en la línea de carga para el circuito de la Figura\(\PageIndex{3}\). Determinar también el valor de\(V_B\).

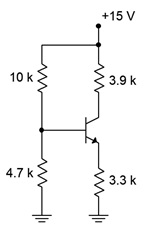
Figura\(\PageIndex{3}\): Circuito por Ejemplo\(\PageIndex{1}\).

Calcular los puntos finales de la línea de carga para que sepamos los máximos.

\[I_{C(sat)} = \frac{V_{CC}}{R_C+R_E} \nonumber \]

\[I_{C(sat)} = \frac{15 V}{3.9K \Omega +3.3K \Omega} \nonumber \]

\[I_{C(sat)} = 2.08mA \nonumber \]

\[V_{CE (cutoff )} = V_{CC} \nonumber \]

\[V_{CE (cutoff )} = 15 V \nonumber \]

Para obtener el punto Q, primero encuentra los valores de Thevenin.

\[V_{TH} = V_{CC} \frac{R_2}{R_1+R_2} \nonumber \]

\[V_{TH} = 15 V \frac{4.7k\Omega}{ 10 k\Omega +4.7 k\Omega} \nonumber \]

\[V_{TH} = 4.8V \nonumber \]

\[R_{TH} = R_1 ∣∣ R_2 = \frac{R_1 R_2}{R_1+R_2} \nonumber \]

\[R_{TH} = \frac{10 k \Omega \times 4.7 k\Omega}{10 k \Omega +4.7 k\Omega} \nonumber \]

\[R_{TH} = 3.2k\Omega \nonumber \]

Usando la ecuación\ ref {5.8}:

\[I_C = \frac{V_{TH} −V_{BE}}{R_E+R_{TH} / \beta} \nonumber \]

\[I_C = \frac{4.8V −0.7V}{3.3 k\Omega +3.2 k\Omega /200} \nonumber \]

\[I_C = 1.236mA \nonumber \]

Observando los tamaños relativos de\(R_E\) y\(R_2\), la aproximación debe ser bastante precisa.

\[I_C = \frac{V_{TH} −V_{BE}}{R_E} \nonumber \]

\[I_C = \frac{4.8V −0.7 V}{3.3k \Omega} \nonumber \]

\[I_C = 1.242mA \nonumber \]

Para encontrar\(V_{CE}\) podemos usar la Ecuación\ ref {5.9}.

\[V_{CE} = V_{CC} −I_C (R_C+R_E ) \nonumber \]

\[V_{CE} = 15V −1.236mA(3.9k \Omega +3.3 k \Omega ) \nonumber \]

\[V_{CE} = 6.1V \nonumber \]

En lo\(V_B\) que respecta a hallazgo, una aproximación decente sería el valor de\(V_{TH}\) porque hemos determinado que el divisor está ligeramente cargado. En un sentido más general, también podríamos encontrar la caída a través\(R_E\) y luego agregar\(V_{BE}\). La aproximación produce 4.8 voltios y el método más preciso rinde

\[V_B = V_{BE} +I_C R_E \nonumber \]

\[V_B = 0.7 V +1.236mA\times 3.3k \Omega \nonumber \]

\[V_B = 4.78V \nonumber \]

La línea de carga para el circuito en Ejemplo\(\PageIndex{1}\) se muestra en la Figura\(\PageIndex{4}\).

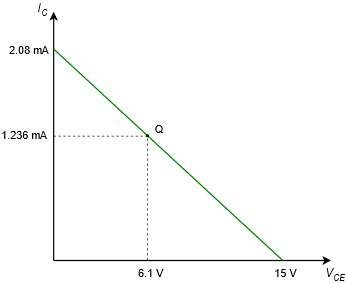
Figura\(\PageIndex{4}\): Línea de carga de CC para el circuito de la Figura\(\PageIndex{3}\).

Una vez más, las proporciones entre voltaje y corriente para el punto Q parecen ser adecuadas cuando se comparan con los puntos finales.

5.4.1: Verificación de Estabilidad

¿Cuánto se mueve el punto Q si\( \beta \) se cortara a la mitad? Recalculando con un\( \beta \) de 100 rendimientos\(I_C = 1.23\) mA y\(V_{CE} = 6.14\) V. Esto representa un desplazamiento tanto en corriente como en voltaje de menos de 1%. Esto, por supuesto, provocará una casi duplicación de\(I_B\) pero esto difícilmente se notará aquí ya que la corriente divisoria es mucho mayor; aproximadamente 15V/ (10 k + 4.7 k) o 1 mA versus aproximadamente 1.23 mA/100 o 12.3\(\mu\) A.

5.4.2: Polarización del divisor de voltaje PNP

Para crear la versión PNP de la polarización del divisor de voltaje, reemplazamos el NPN por un PNP y luego cambiamos el signo de la fuente de alimentación. Como se mencionó con la polarización del emisor de dos fuentes, estos circuitos generalmente se voltean de arriba a abajo dando como resultado que el flujo de corriente CC descienda por la página. Todas las corrientes y voltajes de los componentes no cambian excepto que sus direcciones y polaridades están invertidas. Las ecuaciones actuales y así sucesivamente siguen siendo válidas. Algo un poco extraño sucede con la polarización del divisor de voltaje, sin embargo: terminamos con tierra siendo el potencial más positivo y un suministro negativo en la parte inferior del esquema. Funciona, pero es un problema si estamos usando un suministro positivo tradicional en otra parte del circuito. Después de todo, ¿por qué tener dos suministros donde uno va a hacer? Resulta que podemos hacer una versión de suministro positiva con bastante facilidad. Todo lo que tenemos que hacer es agregar la magnitud del voltaje negativo de la fuente a las conexiones de tierra y alimentación. Esta progresión se muestra en la Figura\(\PageIndex{5}\).

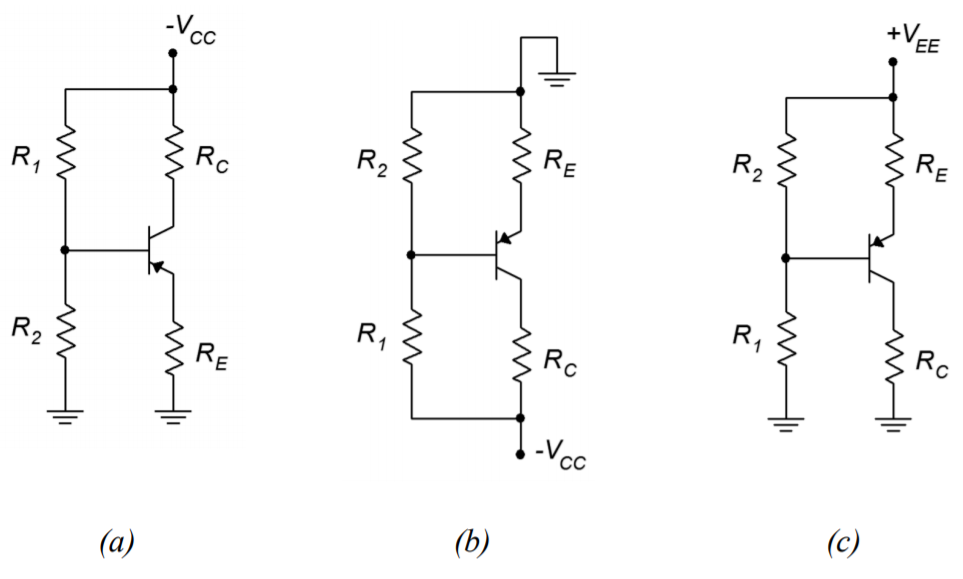
Figura\(\PageIndex{5}\): Progresión del circuito de polarización del divisor de voltaje PNP. a. Conversión directa de NPN. b. flip de arriba a abajo. c. compensación de alimentación de CC agregada para lograr un suministro positivo.

No hay nada de magia en este procedimiento. En esencia, todo lo que realmente hemos hecho es renombrar el punto de referencia. Todos los voltajes de los componentes individuales permanecen sin cambios. Por ejemplo, mirando Figura\(\PageIndex{5c}\) versus\(\PageIndex{5b}\), sigue siendo el caso de que la conexión superior a\(R_E\) es más positiva que la conexión inferior a\(R_C\) por el voltaje\(V_{CC}\) (aunque sí renombramos el suministro\(V_{EE}\) para que sea consistente con donde está conectado). Lo que ha ocurrido es que todos los voltajes referenciados a tierra (es decir, subíndice único) han cambiado. Por ejemplo,\(V_B\) en Figuras\(\PageIndex{5a}\) y\(\PageIndex{5b}\) es el voltaje a través\(R_2\). En contraste,\(V_B\) en la Figura\(\PageIndex{5c}\) se encuentra el voltaje a través\(R_1\). Eso tiene sentido. Si movemos la referencia entonces cualquier voltaje que se mida contra la referencia cambiará.

Al analizar el divisor de voltaje PNP, simplemente podríamos lorar la fórmula de corriente de colector desarrollada para el NPN, pero existen otras técnicas. Dos métodos se ilustran en el siguiente ejemplo.

Ejemplo\(\PageIndex{2}\)

Suponiendo\( \beta = 200\), determinar el punto Q (\(I_C\)y\(V_{CE}\)) para el circuito de la Figura\(\PageIndex{3}\). También determinar los valores de\(V_C\) y\(V_B\).

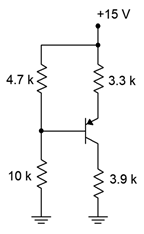
Figura\(\PageIndex{6}\): Circuito por Ejemplo\(\PageIndex{2}\).

En primer lugar,\(R_2\) (ahora en la parte superior) tiene aproximadamente el mismo tamaño,\(R_E\) por lo que el método de aproximación debe ser exacto y podemos suponer que el divisor está ligeramente cargado.

Método Uno

Nos centraremos en el bucle base-emisor como de costumbre porque\(V_{BE}\) es un potencial conocido. Nuestro objetivo inmediato es encontrar el voltaje a través\(R_E\) para que podamos usar la ley de Ohm para encontrar\(I_C\). Primero observamos que la caída de voltaje a través\(R_2\) es igual a las caídas combinadas a través\(R_E\) y\(V_{BE}\). La caída a través\(R_2\) se encuentra a través de la regla del divisor de voltaje.

\[V_{R_2} = V_{EE} \frac{R_2}{R_1+R_2} \nonumber \]

\[V_{R_2} = 15 V \frac{4.7k \Omega}{ 10 k \Omega +4.7k \Omega} \nonumber \]

\[V_{R_2} = 4.8 V \nonumber \]

Y

\[V_{R_E} = V_{R_2} −V_{BE} \nonumber \]

\[V_{R_E} = 4.8V−0.7V \nonumber \]

\[V_{R_E} = 4.1V \nonumber \]

Por lo tanto

\[I_C = \frac{V_{R_E}}{R_E} \nonumber \]

\[I_C = \frac{4.1 V}{3.3 k\Omega} \nonumber \]

\[I_C = 1.24 mA \nonumber \]

Método Dos

Aquí determinaremos todos los voltajes con respecto a tierra.

\[V_B = V_{EE} \frac{R_1}{R_1+R_2} \nonumber \]

\[V_B = 15 V \frac{10 k\Omega}{10 k \Omega +4.7 k\Omega} \nonumber \]

\[V_B = 10.2 V \nonumber \]

El voltaje de base a emisor tiene una polaridad − a +, lo que significa que es un aumento de 0.7 voltios. Por lo tanto

\[V_E = V_B+V_{BE} \nonumber \]

\[V_E = 10.2V+0.7V \nonumber \]

\[V_E = 10.9V \nonumber \]

El voltaje a través\(R_E\) es la diferencia entre\(V_{EE}\) y\(V_E\).

\[V_{R_E} = V_{EE}−V_E \nonumber \]

\[V_{R_E} = 15 V−10.9 V \nonumber \]

\[V_{R_E} = 4.1V \nonumber \]

Este es el mismo valor al que llegamos usando el método uno, por lo que la corriente del colector debe ser la misma a 1.24 mA.

Para encontrar también\(V_{CE}\) tenemos opciones. Una ruta es usar una ecuación ligeramente modificada\ ref {5.9}.

\[V_{CE} = −(V_{EE} −I_C (R_C+R_E )) \nonumber \]

\[V_{CE} = −15V +1.24 mA (3.9 k\Omega +3.3 k\Omega ) \nonumber \]

\[V_{CE} = −6.07V \nonumber \]

El colector es negativo con relación al emisor, de ahí el signo negativo. Para evitar esto, podríamos simplemente intercambiar los leads y referirnos\(V_{EC}\) en su lugar.

Como alternativa, podríamos encontrar\(V_{CE}\) determinando\(V_C\) y luego restando\(V_E\) de ella.

\[V_C = I_C R_C \nonumber \]

\[V_C = 1.24 mA\times 3.9 k\Omega \nonumber \]

\[V_C = 4.84 V \nonumber \]

\[V_{CE} = V_C−V_E \nonumber \]

\[V_{CE} = 4.84 V−10.9 V \nonumber \]

\[V_{CE} = −6.06V \nonumber \]

Aquí vemos una diferencia muy leve debido a errores de redondeo llevados.

Es instructivo comparar los resultados de Ejemplo de\(\PageIndex{2}\) nuevo a Ejemplo\(\PageIndex{1}\). Estos circuitos son por lo demás idénticos excepto por el hecho de que uno es NPN y el otro es PNP. Encontramos los mismos resultados para las corrientes del dispositivo (\(I_C\)) y las magnitudes de voltaje de los componentes (\(V_{CE}\)o el voltaje\(R_E\) transversal); solo se invierten los signos y direcciones. Por otro lado, encontramos que los potenciales referenciados a tierra como\(V_B\),\(V_C\) y\(V_E\) son decididamente diferentes entre los dos circuitos.