6.5: Teorema de Miller
- Page ID
- 83434
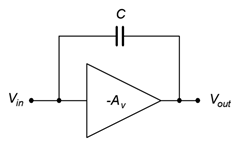
Algunos diseños de amplificadores de voltaje invertidos emplean una impedancia puenteada entre la entrada y la salida, como se muestra en la Figura\(\PageIndex{1}\).
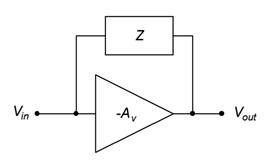
Figura\(\PageIndex{1}\): Impedancia puenteada de entrada/salida.
Hay diferentes razones para hacer esto, un excelente ejemplo que implica dar forma a la respuesta de frecuencia del amplificador. Para simplificar el análisis de dicha configuración, podemos emplear el Teorema de Miller, que lleva el nombre del ingeniero estadounidense John Milton Miller.
El objetivo aquí es determinar impedancias equivalentes que se encuentran en paralelo con la entrada y salida del amplificador. Estos equivalentes simplemente se convierten en parte de las redes de entrada y salida alrededor del amplificador.
Primero, consideremos la impedancia equivalente en la entrada,\(Z_{in-miller}\). Por definición, esta es la impedancia en paralelo con la entrada del amplificador que extraería la misma cantidad de corriente que la impedancia original de Miller puente. La corriente a través de la impedancia Miller es simplemente el voltaje a través de ella dividido por la impedancia Miller,\(Z\). El voltaje a través de él es la diferencia entre los voltajes de entrada y salida.
\[i_{in−miller} = \frac{V_{i n} −V_{out}}{Z} \nonumber \]
\[i_{in−miller} = \frac{V_{i n} - A_v V_{in}}{Z}, \text{ the gain is negative so} \nonumber \]
\[i_{in−miller} = \frac{V_{i n} (|A_v| +1)}{Z} \nonumber \]
Al dividir esta corriente en el voltaje de entrada se obtiene la impedancia equivalente.
\[Z_{i n−miller} = \frac{Z}{∣A_v ∣+1} \nonumber \]
Una derivación similar produce el equivalente de salida.
\[Z_{out−miller} = \frac{Z∣A_v ∣}{∣A_v ∣+1} \nonumber \]
El circuito equivalente Miller para una impedancia general\(Z\) se muestra en la Figura\(\PageIndex{2}\).
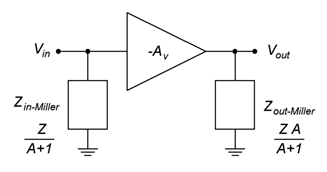
Figura\(\PageIndex{2}\): Equivalente general Miller.
La regla general a recordar es que el equivalente Miller presenta impedancias equivalentes que son menores que la impedancia de puente original. En el caso de la sección de entrada, el efecto de reducción es muy grande a mayores ganancias.
Dos casos típicos para la impedancia\(Z\) son una resistencia,\(R\), y una capacitancia,\(C\). Por una resistencia pura, podemos realizar una sustitución directa de\(Z\). Los equivalentes originales y Miller se muestran en la Figura\(\PageIndex{3}\).
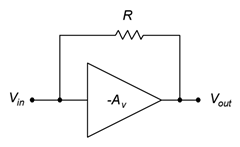
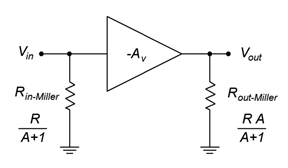
Figura\(\PageIndex{3}\): Original y equivalente Miller para una resistencia.
Para un condensador, la situación es similar, sin embargo, lo\(X_c\) sustituiremos\(Z\) y recordaremos\(C = 1/(2\pi fX_c)\).
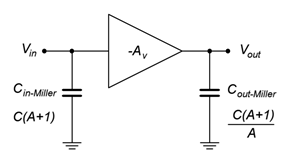
Figura\(\PageIndex{4}\): Original y equivalente Miller para un condensador.
Tenga en cuenta que para el condensador, hay un efecto multiplicativo. Es decir, el efecto del condensador de puente original en un amplificador de alta ganancia es equivalente a un condensador de derivación de entrada mucho más grande.


