7.4: Amplificador de colector común
- Page ID
- 83513
El amplificador colector común a menudo se conoce como seguidor de emisor, o más genéricamente, como seguidor de voltaje. Las características clave de un seguidor de voltaje son una alta impedancia de entrada, una baja impedancia de salida y una ganancia de voltaje no inversora de aproximadamente una. El nombre proviene del hecho de que el voltaje de salida sigue a la entrada, es decir, está al mismo nivel de voltaje y está en fase con la entrada. Si bien esta configuración no produce ganancia de voltaje, produce ganancia de corriente y, por lo tanto, ganancia de potencia. Su propósito principal es reducir los efectos de carga de impedancia, por ejemplo, para hacer coincidir una fuente de alta impedancia con una carga de baja impedancia. En consecuencia, se utilizan como etapas de búfer de entrada de alto Z o como controladores para cargas de baja impedancia como altavoces.
Un amplificador colector común que utiliza polarización de emisor de dos fuentes se muestra en la Figura\(\PageIndex{1}\). La entrada se acopla a la base como el amplificador emisor común, sin embargo, la señal de salida se toma en el emisor en lugar de en el colector. Debido a que el colector está en la CA común, no hay necesidad de una resistencia de colector.
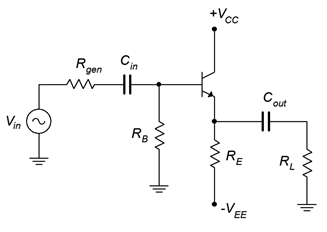
Figura\(\PageIndex{1}\): Amplificador colector común.
Quizás la mejor manera de pensar en el seguidor no es que le dé una ganancia de voltaje de uno, sino que evitará la pérdida de señal. A continuación se realiza el análisis, utilizando la Figura\(\PageIndex{2}\).
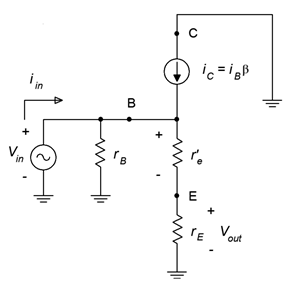
Figura\(\PageIndex{2}\): Equivalente de CA del amplificador colector común.
Primero, la resistencia del emisor de CA\(r_E\), es la resistencia de polarización del emisor\(R_E\), o la combinación paralela de\(R_E\) y la resistencia de carga,\(R_L\). Usaremos el primero para determinar la ganancia descargada y el segundo para determinar la ganancia cargada, similar a lo que hicimos con el amplificador emisor común concerniente\(R_C\) y\(R_L\). La resistencia de la base de CA\(r_B\), generalmente se reduce a la resistencia de polarización base tal como vimos con el amplificador emisor común (\(R_B\)en una polarización de emisor de dos fuentes o\(R_1 || R_2\) para una polarización de divisor de voltaje).
7.4.1: Ganancia de voltaje
La derivación para la ecuación de ganancia de voltaje del seguidor de emisor es similar a la que se muestra para el amplificador emisor común. Comenzamos con la definición básica de ganancia de voltaje y luego expandimos usando la ley de Ohm.
\[A_v = \frac{v_{out}}{v_{i n}} = \frac{v_E}{v_B} \\ A_v = \frac{i_C r_E}{i_C (r'_e+r_E )} \\ A_v = \frac{r_E}{r'_e+r_E} \label{7.8} \]
Esta ecuación es muy similar a la de la Ecuación 7.3.1. Aquí vemos que la señal de salida está en fase con la entrada y que si\(r_E \gg r'_e\), la ganancia se acerca a la unidad. La distorsión de la señal tiende a ser baja en seguidores porque una ganancia de uno es un objetivo deseado.
7.4.2: Impedancia de entrada
La derivación para\(Z_{in}\) y\(Z_{in(base)}\) no cambia en comparación con la configuración común del emisor. Las fórmulas se repiten a continuación para mayor comodidad.
\[Z_{in(base)} = \beta (r'_e + r_E) \nonumber \]
\[Zin = r_B || Z_{in(base)} \nonumber \]
7.4.3: Impedancia de salida
La derivación para la impedancia de salida del colector común varía considerablemente de la del emisor común. Utilizaremos Figura\(\PageIndex{3}\) para el análisis.
Primero, tenga en cuenta que este diagrama divide la resistencia del emisor de CA en sus dos componentes,\(R_L\) y la resistencia de polarización\(R_E\). Esto se debe a que queremos encontrar la resistencia efectiva de la fuente que impulsa la carga, por lo que lógicamente no podemos incluir la carga en ese valor. Comenzamos por mirar hacia atrás en el emisor desde la perspectiva de la carga. Vemos la resistencia de polarización del emisor en paralelo con lo que sea que la impedancia esté mirando hacia atrás en el terminal del emisor.
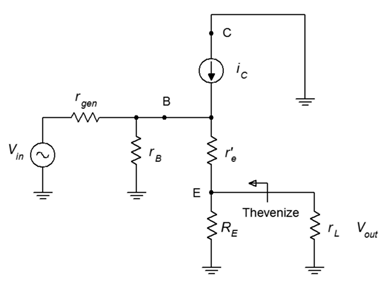
Figura\(\PageIndex{3}\): Análisis de impedancia de salida de colector común.
\[Z_{out} = R_E || Z_{out(emitter)} \label{7.9} \]
\(Z_{out(emitter)}\)es igual a\(r'_e\) en serie con la resistencia equivalente de la red por encima de ella y a la izquierda. La resistencia interna de la fuente de corriente es lo suficientemente alta como para ignorarla así que nos quedamos con la resistencia equivalente mirando hacia atrás fuera de la base. A esto lo llamaremos\(Z_{B(equivalent)}\). A primera vista, esta podría parecer la combinación paralela de\(r_{gen}\) y\(r_B\), pero esto ignora el efecto de la fuente de corriente del colector. Lo que realmente queremos es la resistencia efectiva como se ve desde la perspectiva de\(r'_e\), no como se ve desde el terminal base.
\[Z_{out (emitter)} = r'_e+Z_{B( equivalent)} \label{7.10} \]
\[Z_{B(equivalent)} = \frac{v_B}{i_C} \\ Z_{B(equivalent)} = \frac{i_B (r_B || r_gen)}{ \beta i_B} \\ Z_{B(equivalent)} = \frac{r_B || r_{gen}}{ \beta } \label{7.11} \]
Combinando ecuaciones\ ref {7.9},\ ref {7.10} y\ ref {7.11} rendimientos
\[Z_{out} = R_E || \left( r'_e + \frac{r_B || r_{gen}}{ \beta } \right) \label{7.12} \]
En muchos casos, la resistencia de polarización del emisor es lo suficientemente grande como para ignorarla.
Ejemplo\(\PageIndex{1}\)
Para el seguidor mostrado en la Figura\(\PageIndex{4}\), determine la impedancia de entrada, la impedancia de salida y el voltaje de carga. Asumir\( \beta = 100\) y\(V_{in} = 100\) mV.
Primero,\(I_C\) encuentra para encontrar\(r'_e\). Suponiendo un divisor descargado,\(V_B\) será igual a la mitad de la fuente de CC, o 10 voltios. Perdemos 0.7 voltios a través de la unión base-emisor dejando 9.3 voltios a través de los 10 k\( \Omega \). Esto da como resultado una corriente de colector de 930\(\mu\) A y una\(r'_e\) de 28\( \Omega \).
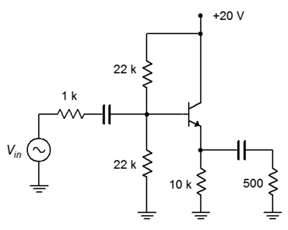
Figura\(\PageIndex{4}\): Esquemática por ejemplo\(\PageIndex{1}\).
Para encontrar\(Z_{in}\)
\[Z_{i n(base)} = \beta (r'_e+r_E ) \nonumber \]
\[Z_{i n(base)} = 100(28 \Omega +10 k \Omega || 500 \Omega ) \nonumber \]
\[Z_{i n(base)} = 50.4 k \Omega \nonumber \]
\[Z_{i n} = R_1 || R_2 || Z_{i n(base )} \nonumber \]
\[Z_{i n} = 22 k \Omega || 22k \Omega || 50.4 k \Omega \nonumber \]
\[Z_{i n} = 9.03k \Omega \nonumber \]
Este valor no es particularmente alto cuando se compara con la resistencia de fuente bastante grande de 1 k\( \Omega \). Habrá alguna pérdida de señal aquí debido al efecto divisor de voltaje entre las dos impedancias. Y ahora para\(Z_{out}\)
\[Z_{out} = R_E || \left( r'_e + \frac{r_B || r_{gen}}{ \beta} \right) \nonumber \]
\[Z_{out} = 10 k \Omega || \left( 28 \Omega + \frac{22k \Omega || 22 k \Omega || 1k \Omega}{100} \right) \nonumber \]
\[Z_{out} = 37 \Omega \nonumber \]
Este valor es mucho, mucho menor que cualquier cosa que vimos con los amplificadores emisores comunes. Por lo tanto, este circuito puede impulsar cargas de impedancia mucho más bajas con pérdida de señal mínima. La ganancia cargada de la base al emisor es
\[A_v = \frac{r_E}{r'_e+r_E} \nonumber \]
\[A_v = \frac{500 \Omega || 10 k \Omega}{28 \Omega +500 \Omega || 10 k \Omega} \nonumber \]
\[A_v = 0.9444 \nonumber \]
Como se mencionó, necesitamos incluir el efecto de la impedancia de la\( \Omega \) fuente de 1 k. Esto creará un divisor de voltaje con la impedancia de entrada.
\[A_{divider} = \frac{Z_{in}}{Z_{i n}+Z_{source}} \nonumber \]
\[A_{divider} = \frac{9.03 k \Omega}{9.03k \Omega +1 k \Omega} \nonumber \]
\[A_{divider} = 0.9 \nonumber \]
\[A_{v (system)} = A_v\times A_{divider} \nonumber \]
\[A_{v (system)} = 0.9444\times 0.9 \nonumber \]
\[A_{v (system)} = 0.85 \nonumber \]
Por último, llegamos a la tensión de carga.
\[V_{load} = A_{v (system)} \times V_{i n} \nonumber \]
\[V_{load} = 0.85\times 100mV \nonumber \]
\[V_{load} = 85mV \nonumber \]
En este punto la pregunta podría ser: “¿Por qué nos tomamos la molestia de construir este circuito cuando perdimos el 15% de la señal de entrada?” Bueno, considera lo que hubiera pasado sin el circuito. Si hubiéramos conectado la fuente directamente a la carga, el divisor de\( \Omega \) voltaje resultante de 1\( \Omega \) k/500 habría bajado el voltaje de carga a 33 mV. Este circuito evitó esa pérdida.
7.4.4: Una fuente de alta impedancia: La pastilla de guitarra
En Ejemplo\(\PageIndex{1}\), la fuente tenía una impedancia interna de 1 k\( \Omega \), mucho mayor de lo que veríamos con, digamos, un generador de funciones de laboratorio (probablemente 50\( \Omega \)). Las cosas podrían ser mucho peores. Considera la pastilla de guitarra eléctrica. El trabajo de una pastilla es transformar las vibraciones de las cuerdas de guitarra en una señal eléctrica para que pueda ser amplificada. Comúnmente se piensa que una pastilla es alguna forma de micrófono pero esto no es cierto 1.
Una pastilla de guitarra es poco más que un imán rodeado de numerosas vueltas de alambre fino, como se muestra en la Figura\(\PageIndex{5}\). Esta particular pastilla es para un bajo pero la construcción es similar para todo tipo de guitarras y bajos.

Figura\(\PageIndex{5}\): Pastilla eléctrica de bajo (cubierta quitada).
Así es como funciona: El imán crea un campo alrededor de las cuerdas de la guitarra. Debido a que las cuerdas son de acero, su reticencia es mucho menor que el aire circundante, por lo tanto, distorsionan o doblan el campo magnético. Cuando se arranca una cuerda, el campo se mueve hacia adelante y hacia atrás junto con ella. A medida que el campo se mueve, las líneas de flujo atraviesan el cable de la bobina y esta acción induce una corriente en el conductor de acuerdo con la Ley de Inducción de Faraday. Esta corriente es luego alimentada al amplificador.
Una pastilla de guitarra típica consiste en quizás 5000 vueltas de alambre muy fino, siendo 42 AWG típico. El cable de cobre de calibre 42 tiene una resistencia de alrededor de 1.6\( \Omega \) por pie por lo que la resistencia de CC de la bobina puede ser superior a 5 k\( \Omega \). Además, que muchas vueltas de alambre alrededor de un imán pueden producir una inductancia muy grande, quizás varios henries, que está en serie con esta resistencia. También hay capacitancia distribuida y capacitancia de cable en paralelo que podría ser superior a 1 nF. El resultado es una impedancia compleja con efectos de resonancia, regiones de las cuales pueden ser decenas de k\( \Omega \) de magnitud. Lo que hace que esto sea más desafiante es que debido a que la impedancia es una función de la frecuencia, el efecto divisor de voltaje con la impedancia de entrada del amplificador también se convierte en una función de la frecuencia. Por ejemplo, el aumento de la impedancia debida a\(X_L\) dará como resultado un aumento de la atenuación con la frecuencia. Esto es similar a bajar los agudos en el amplificador. Generalmente, no es un buen resultado. ¿Cómo limitamos este efecto? Sencillo. Hacemos un circuito con una impedancia de entrada muy, muy alta. ¿Cómo lo hacemos? Bueno, hay varias formas, entre ellas el uso de transistores de efecto de campo y amplificadores operacionales, pero también podemos obtener altas impedancias de entrada mediante el uso de una configuración dual BJT llamada par Darlington.
7.4.5: El par Darlington
La pareja Darlington fue inventada por Sidney Darlington, un ingeniero estadounidense. La configuración conduce a un dispositivo compuesto con una muy alta\( \beta \). Usado correctamente, esto puede conducir a circuitos amplificadores con impedancia de entrada muy alta. Un par Darlington se muestra en la Figura\(\PageIndex{6}\).
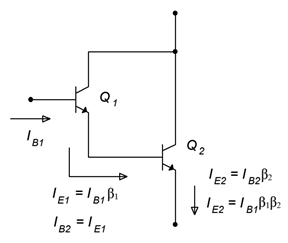
Figura\(\PageIndex{6}\): Par Darlington.
La operación es la siguiente. La corriente base del primer transistor,\(Q_1\), se multiplica por la\( \beta \) de\(Q_1\) resultante en\(Q_1\) la corriente del emisor. Esta corriente se alimenta a la base del segundo transistor,\(Q_2\), donde se multiplica por la\( \beta \) de\(Q_2\) resultante en\(Q_2\) la corriente del emisor. Si tratamos el par como un solo dispositivo, entonces el efectivo\( \beta \) del par es\( \beta _1 \beta _2\). Dados los valores típicos para\( \beta \), el valor compuesto puede estar en las proximidades de 5000 a 10,000. La desventaja funcional de esta disposición\(V_{BE}\) es que ahora se duplica a 1.4 voltios (para silicio) y la efectividad\(r'_e\) del par también se duplica. Estos temas son menores cuando se comparan con la ventaja de la enorme ganancia de corriente que se puede obtener.
El resultado final al usar un par Darlington es tratarlo como un transistor ordinario excepto que tiene un muy grande\( \beta \) y ambos\(V_{BE}\) y se\(r'_e\) duplican en comparación con los valores ordinarios.
Ejemplo\(\PageIndex{2}\)
Determine el voltaje de salida para el seguidor que se muestra en la Figura\(\PageIndex{7}\). Supongamos que la entrada es de pico de 100 mV y la\( \beta \) para el par Darlington es 10,000.
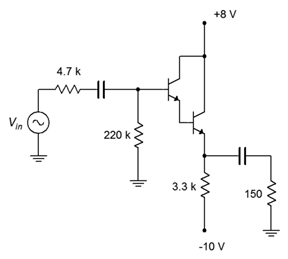
Figura\(\PageIndex{7}\): Esquemática por ejemplo\(\PageIndex{2}\).
Lo primero que podría parecer un poco extraño, al menos en comparación con los circuitos de polarización anteriores, es que la resistencia de polarización de base es mucho más grande que la resistencia de polarización del emisor. Normalmente, esto llevaría a un punto Q inestable pero eso no es un problema aquí. Porque\( \beta \) es tan grande,\(R_B\) puede ser mucho más grande de lo normal y aún así lograremos una buena estabilidad. De hecho, todavía podemos usar la aproximación de que la base está en tierra CC. Siendo esto cierto, el análisis procede de la siguiente manera
\[I_C = \frac{∣V_{EE} ∣−V_{BE}}{R_E} \nonumber \]
\[I_C = \frac{10 V−1.4 V}{3.3 k \Omega} \nonumber \]
\[I_C = 2.61mA \nonumber \]
\[r'_e = 2\times \frac{ 26mV}{I_C} \nonumber \]
\[r'_e = \frac{52 mV}{2.61mA} \nonumber \]
\[r'_e = 20 \Omega \nonumber \]
\[Z_{i n(base)} = \beta (r'_e+r_E ) \nonumber \]
\[Z_{i n(base)} = 10,000(20 \Omega +3.3k \Omega || 150 \Omega ) \nonumber \]
\[Z_{i n(base)} = 1.63M \Omega \nonumber \]
Este valor está en paralelo con la resistencia de polarización base, creando la impedancia de entrada.
\[Z_{i n} = R_B || Z_{i n(base)} \nonumber \]
\[Z_{i n} = 220 k \Omega || 1.63M \Omega \nonumber \]
\[Z_{i n} = 194 k \Omega \nonumber \]
Esto es mucho más alto de lo que hemos visto en circuitos anteriores. La ganancia cargada de la base al emisor es
\[A_v = \frac{r_E}{r'_e+r_E} \nonumber \]
\[A_v = \frac{150 \Omega || 3.3k \Omega}{20 \Omega +150 \Omega || 3.3k \Omega} \nonumber \]
\[A_v = 0.88 \nonumber \]
Ahora para incluir el efecto de la impedancia de la\( \Omega \) fuente de 4.7 k. Esto creará un divisor de voltaje con la impedancia de entrada, mínima como resulta.
\[A_{divider} = \frac{Z_{in}}{Z_{i n} + Z_{source}} \nonumber \]
\[A_{divider} = \frac{194 k \Omega}{ 194 k \Omega +4.7 k \Omega} \nonumber \]
\[A_{divider} = 0.976 \nonumber \]
\[A_{v (system)} = A_v\times A_{divider} \nonumber \]
\[A_{v (system)} = 0.88\times 0.976 \nonumber \]
\[A_{v (system)} = 0.86 \nonumber \]
El voltaje de carga es
\[V_{load} = A_{v (system)}\times V_{i n} \nonumber \]
\[V_{load} = 0.86\times 100mV \nonumber \]
\[V_{load} = 86mV \nonumber \]
Si hubiéramos conectado la fuente directamente a la carga, el\( \Omega \) divisor de 4.7\( \Omega \) k/150 habría aplastado la señal aplicada en una sombra de su tamaño anterior, dejándonos con apenas 3 mV.
Simulación por Computadora
Para verificar los resultados de Ejemplo\(\PageIndex{2}\), realizaremos un análisis transitorio. El esquema de entrada se muestra en la Figura\(\PageIndex{8}\).
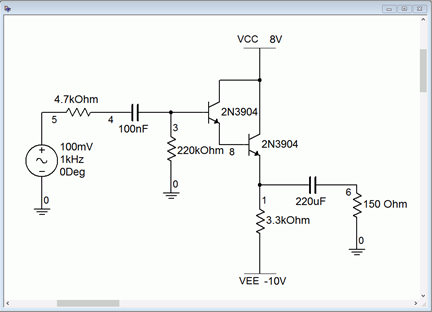
Figura\(\PageIndex{8}\): Esquema de simulación para seguidor de par Darlington.
De interés aquí serán los voltajes en la fuente, base y carga. Como el divisor de impedancia de entrada/fuente de impedancia fue de 0.976, esperamos 97.6 mV en el nodo 4. En la salida, nodo 6, esperamos ver nuestro valor final calculado de 86 mV. La gráfica de salida de la simulación se muestra en la Figura\(\PageIndex{9}\). La simulación concurre.
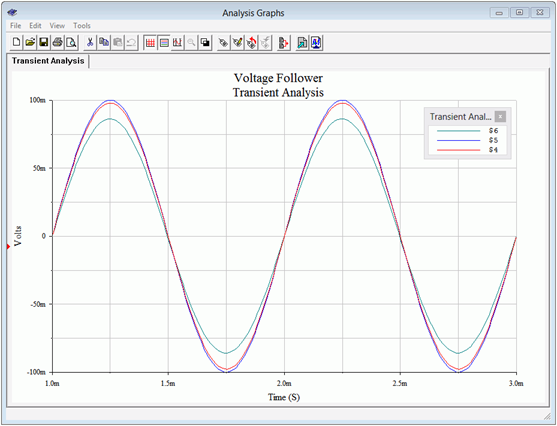
Figura\(\PageIndex{9}\): Análisis transitorio para seguidor de par Darlington.
7.4.6: El divisor de fase
Un divisor de fase es una combinación de un amplificador emisor común y un seguidor de colector común que utiliza un solo transistor. El propósito del circuito es producir dos versiones de la señal de entrada: una versión en búfer idéntica a la entrada y una versión invertida, teniendo ambas ondas la misma amplitud. El circuito se utiliza para sistemas de controlador de línea diferencial. Este esquema ayuda a minimizar el ruido exterior y las interferencias captadas por los cables de comunicaciones. Hay otras formas de crear divisores de fase, incluyendo el uso de amplificadores diferenciales o amplificadores operacionales, pero esta versión basada en BJT es una solución minimalista 2. El circuito básico se muestra en la Figura\(\PageIndex{10}\).
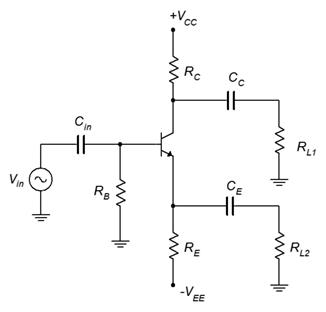
Figura\(\PageIndex{10}\): Un divisor de fase simple.
Para un correcto funcionamiento, el circuito es en gran parte simétrico. Es decir,\(R_{L1} = R_{L2}\),\(R_E = R_C\), y\(C_C = C_E\). Siendo ese el caso, las resistencias del colector de CA y del emisor serán iguales (\(r_C = r_E\)). Si luego miramos las ecuaciones básicas de ganancia, encontramos que ambas cargas recibirán la misma magnitud de ganancia (justo por debajo de la unidad), aunque\(R_{L1}\) veremos la señal invertida.
\[A_v =− \frac{r_C}{r'_e+r_E} \text{ Common emitter amplifier} \nonumber \]
\[A_v = \frac{r_E}{r'_e+r_E} \text{ Common collector follower} \nonumber \]
Referencias
1 ¿No lo crees? Solo intenta gritar en uno y escucha lo que sale del amplificador de guitarra.
2 Para obtener detalles sobre métodos alternativos, consulte Fiore, J, Amplificadores Operacionales y Circuitos Integrados Lineales: Teoría y Aplicación, otro texto libre de REA.


