7.6: Amplificadores multietapa

Para lograr una ganancia mayor de la que podemos obtener de una sola etapa, es posible poner en cascada dos o más etapas. Se pueden usar diferentes tipos de polarización junto con una mezcla de configuraciones de CA, como un seguidor de colector común para la primera etapa que impulsa un amplificador de voltaje de emisor común. También puede estar presente una mezcla de dispositivos NPN y PNP.

En términos generales, cada etapa sirve como carga para la etapa anterior. Es decir, el\(Z_{in}\) de una etapa es el\(R_L\) de la etapa anterior. Las ganancias de las etapas individuales se multiplican luego juntas para llegar a la ganancia del sistema. La impedancia de entrada del sistema es la impedancia de entrada de la primera etapa solamente. La fuente impulsa la primera etapa sola. La primera etapa, a su vez, impulsa la segunda etapa, y así sucesivamente. Por lo tanto la fuente sólo “ve” la primera etapa porque es la única etapa a la que entrega corriente. De manera similar, la impedancia de salida del sistema es la\(Z_{out}\) de la última etapa. Un ejemplo se muestra en la Figura\(\PageIndex{1}\).

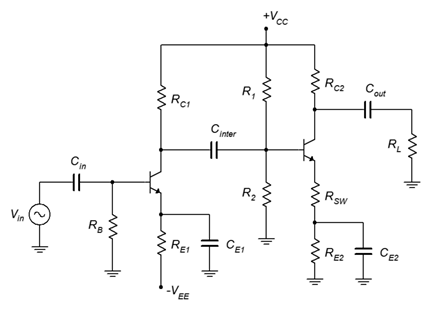
Figura\(\PageIndex{1}\): Amplificador de dos etapas.

En este circuito, la etapa uno es un amplificador de emisor común no inundado que utiliza polarización de emisor de dos fuentes. La segunda etapa es un amplificador emisor común inundado que utiliza polarización del divisor de voltaje. En lo que respecta al análisis de CC, se trata de dos circuitos separados. El condensador de acoplamiento entre etapas\(C_{inter}\), evita que el potencial de CC en el colector del primer transistor interfiera con la polarización establecida por\(R_1\) y\(R_2\) para el transistor número dos. Para el cálculo de CA, la primera etapa se analiza de manera normal excepto que su resistencia a la carga está compuesta por\(R_1 || R_2 || Z_{in-base2}\) (es decir,\(Z_{in}\) de la etapa 2). La segunda etapa se analiza sin cambios y su ganancia se multiplica por la ganancia de la primera etapa para llegar a la ganancia final para el par. La impedancia de entrada del sistema es\(R_B || Z_{in-base1}\) (es decir,\(Z_{in}\) de la etapa 1).

Debe ser obvio que al conectar en cascada varias etapas es posible lograr ganancias de sistema muy altas, incluso si cada etapa está fuertemente inundada para reducir la distorsión. Por ejemplo, tres etapas de emisor común inundadas con ganancias de voltaje de solo 10 cada una producirían una ganancia de voltaje del sistema de 1000.

7.6.1: Acoplamiento Directo

Con un poco de creatividad, es posible crear diseños multietapa que utilicen menos componentes pero que logren un mayor rendimiento. Una técnica es emplear el acoplamiento directo de las etapas. El acoplamiento directo permite que la CC fluya de una etapa a otra. Como tal, es posible diseñar un amplificador que no tenga límite de frecuencia inferior. Un ejemplo se muestra en la Figura\(\PageIndex{2}\).

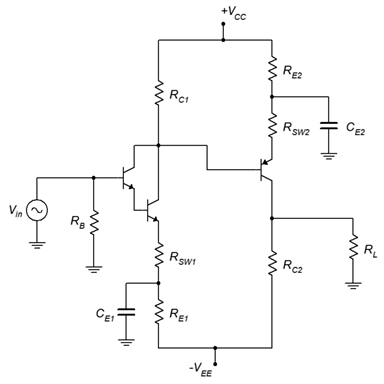
Figura\(\PageIndex{2}\): Amplificador de acoplamiento directo.

Este amplificador de dos etapas no utiliza condensadores de acoplamiento ni se basa en resistencias divisoras de voltaje para la segunda etapa ¹. Así es como funciona: La primera etapa es un amplificador de emisor común inundado bastante ordinario que utiliza polarización de emisor de dos fuentes. También utiliza un par Darlington para maximizar la impedancia de entrada. Debido a que la corriente base es tan baja, la caída de CC\(R_B\) podría ser lo suficientemente pequeña como para ignorarla, por lo que podemos prescindir del condensador de acoplamiento de entrada. El potencial de CC en el colector del Darlington se aplica directamente a la base de la segunda etapa. Esto se utiliza para configurar el sesgo de la segunda etapa a través de las resistencias de emisor de la etapa dos. Esto es precisamente lo que hicimos con el circuito de la Figura 7.3.5. La única diferencia es que aquí el voltaje base se deriva de la etapa anterior en lugar de de un divisor de voltaje. Los cálculos para\(I_C\),\(r'_e\) y similares procederían sin cambios. En cualquier caso, esto elimina dos resistencias de polarización y otro condensador de acoplamiento.

Tenga en cuenta el uso del dispositivo PNP para la segunda etapa. Al usar un PNP, su voltaje de colector debe ser menor que su voltaje de emisor. Como también estamos usando una fuente de alimentación bipolar, podemos eliminar la necesidad del condensador de acoplamiento de salida final. Todo lo que tenemos que hacer es configurar los valores de resistencia de tal manera que la caída transversal\(R_{C2}\) sea la misma que\(V_{EE}\). Esto colocará el voltaje del colector de CC de la etapa dos a 0 voltios. Si no hay voltaje de CC, entonces no hay nada que bloquear y, por lo tanto, no hay necesidad del condensador de acoplamiento.

Referencias

¹ Este circuito utiliza condensadores de derivación del emisor, por lo que la ganancia de CC será menor que la ganancia de CA. En ese sentido podríamos decir que este amplificador no está totalmente acoplado a CC.