10.2: Internos JFET

En la Figura se muestra un modelo interno simplificado de un JFET\(\PageIndex{1}\). La parte principal del dispositivo se llama canal. El diagrama ilustra un dispositivo de canal N. El canal se construye sobre un sustrato (es decir, capa base) de material dopado opuestamente. Conectados a los extremos opuestos del canal hay dos terminales; la fuente y el drenaje. Dentro del canal está incrustada una región que utiliza el tipo de material opuesto. A esto también se le une una pista y se llama la puerta. Aunque no existe una correspondencia perfecta entre ellos, el drenaje, la fuente y la compuerta son aproximadamente análogos al colector, emisor y base del BJT, respectivamente.

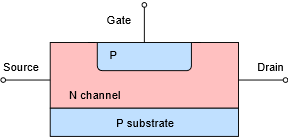
Figura\(\PageIndex{1}\): Estructura interna simplificada de un JFET de canal N.

Este diagrama se dibuja simétricamente. Algunos dispositivos están diseñados de esta manera y sus terminales de drenaje y fuente pueden intercambiarse sin cambios en la operación. Sin embargo, esto no es cierto para todos los dispositivos. Para valores pequeños de voltaje drenaje-fuente, el canal exhibe una cierta cantidad de resistencia que depende del nivel de dopaje y la disposición física del dispositivo. Además, bajo funcionamiento normal,\(I_D\) será igual\(I_S\).

Para entender cómo se comporta el dispositivo, consulte la Figura\(\PageIndex{2}\). Aquí consideraremos el flujo de electrones (mostrado como una línea discontinua). Primero, un voltaje positivo,\(V_{DD}\), se conecta al terminal de drenaje junto con una resistencia limitadora de corriente,\(R_D\). Un suministro negativo,\(V_{GG}\), se aplica al terminal de puerta a través de una resistencia\(R_G\). Comencemos con el suministro de puerta establecido en cero. Si empezamos\(V_{DD}\) en cero, esto es lo que sucede a medida que aumentamos su valor. Inicialmente, un aumento en el voltaje drenaje-fuente provocará un aumento proporcional en la corriente que fluye a través del canal. En otras palabras, el canal actúa como una resistencia. A medida que el voltaje a través de la fuente de drenaje aumenta aún más, en algún momento la corriente se saturará, y no se producirán más aumentos en la corriente a pesar de nuevos aumentos en\(V_{DD}\) y\(V_{DS}\). En este punto el dispositivo se está comportando como una fuente de corriente constante. El voltaje drenaje-fuente donde ocurre esta transición se llama voltaje de pellizco,\(V_p\). Si el voltaje drenaje-fuente aumenta demasiado, se producirá una avería y la corriente comenzará a aumentar rápidamente.

Lo que es particularmente interesante es lo que sucede cuando el suministro de la puerta se incrementa en la dirección negativa. Esto sesga hacia atrás la unión PN puerta-fuente y da como resultado una región de agotamiento más grande que se forma. La región de agotamiento se ensancha en el canal, restringiendo así el flujo de corriente antes y en un nivel más bajo. Cuanto más negativo hacemos\(V_{GG}\), más bajo se\(I_D\) vuelve. Eventualmente, cuando\(V_{GG}\) va lo suficientemente negativo, la corriente de drenaje se apagará. A este voltaje se le llama\(V_{GS(off)}\) y tiene la misma magnitud que\(V_P\) (es decir,\(V_P = |V_{GS(off)}|)\). Se puede pensar que la acción funciona como una válvula de agua: girar el voltaje de la fuente de la compuerta más negativo es como apagar la espita y disminuir el flujo.

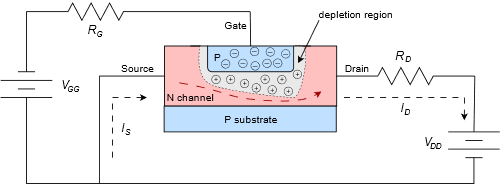
Figura\(\PageIndex{2}\): Flujo de electrones en un JFET de canal N.

El funcionamiento del JFET se puede visualizar muy bien trazando un conjunto de curvas de drenaje, como se muestra en la Figura\(\PageIndex{3}\).

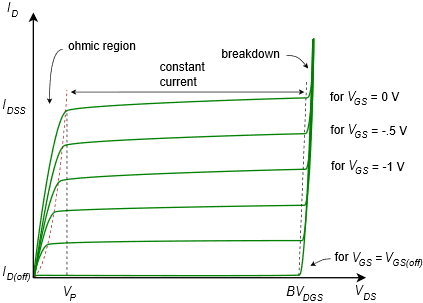
Figura\(\PageIndex{3}\): Curvas de drenaje JFET.

La familia de curvas de drenaje traza la corriente de drenaje\(I_D\), versus el voltaje drenaje-fuente,\(V_{DS}\). Comenzamos con la curva más alta. Esto se genera estableciendo el voltaje puerta-fuente,\(V_{GS}\), a cero. Luego circulamos\(V_{DS}\) de cero a algún valor superior. Inicialmente, vemos un aumento proporcional en\(I_D\) como\(V_{DS}\) aumentos. A esto se le llama región óhmica o triodo. Eventualmente, el canal se satura y la corriente se nivela. Esta es la región de corriente constante o saturación y ocurre para\(V_{DS} > V_P\). El voltaje de ruptura se llama\(BV_{DGS}\), o alternativamente,\(V_{(BR)DS}\). Por encima de este voltaje la corriente aumenta rápidamente. Como es habitual, no deseamos operar el dispositivo en esta región de avería.

Si ahora repetimos el proceso pero esta vez usamos un pequeño valor negativo para\(V_{GS}\), trazaremos una curva de forma muy similar. La transición al modo de corriente constante ocurrirá a un voltaje ligeramente menor y el valor de la corriente también será algo menor. Este proceso continúa de la misma manera a medida que hacemos\(V_{GS}\) cada vez más negativos. Eventualmente, cuando\(V_{GS} = V_{GS(off)}\), la corriente de drenaje cae a prácticamente cero (de hecho, una pequeña corriente de fuga fluye llamada\(I_{D(off)}\)). En contraste, si\(V_{GS}\) se dejara ir positivo, la operación se perdería porque el cruce PN se volvería sesgado hacia adelante y perdería el control de la corriente a través de la región de agotamiento. Esto significa que el control de corriente del JFET está completamente en el segundo cuadrante y la corriente de drenaje más grande fluye cuando se llama\(V_{GS} = 0\) V. Esta corriente es llamada\(I_{DSS}\), que significa la corriente de drenaje con una puerta-fuente en cortocircuito (es decir, si está en cortocircuito, entonces\(V_{GS} = 0\) V). El JFET no puede producir una corriente continua mayor que\(I_{DSS}\) segura.

La ecuación característica que relaciona la corriente de drenaje y el voltaje puerta-fuente se muestra a continuación. Esto es válido para la región de corriente constante (i.e.,\(V_{DS} > V_P\)).

\[I_D = I_{DSS} \left( 1 − \frac{V_{GS}}{V_{GS (off )}} \right)^2 \label{10.1} \]

Dónde

\(V_{GS}\)es la tensión puerta-fuente (\(V_{GS(off)} \leq V_{GS} \leq 0\)),

\(I_D\)es la corriente de drenaje,

\(I_{DSS}\)es la corriente máxima,

\(V_{GS(off)}\)es el voltaje de apagado.

De esto vemos que el JFET es un dispositivo de ley cuadrada más que como el BJT que tiene una característica logarítmica. ¹ En esencia, esta curva es una porción de una parábola. Esto significa que la curva característica del JFET es mucho más gradual en pendiente que la de un BJT. Esto tendrá importantes implicaciones cuando se trata de potencial de ganancia de voltaje y distorsión, como veremos en el siguiente capítulo.

Es útil recordar que\(V_{GS(off)}\) y\(I_{DSS}\) son únicos para un dispositivo dado, más bien como lo\(\beta\) es para un BJT. También puede haber una variación bastante grande en estos parámetros. Por ejemplo, un modelo particular de JFET podría mostrar una\(I_{DSS}\) variación entre 2 mA y 20 mA, y una\(V_{GS(off)}\) variación entre −2 V y −8 V. Generalmente, los\(V_{GS(off)}\) valores más negativos se asociarán con los\(I_{DSS}\) valores más grandes.

La ecuación\ ref {10.1} se traza en la Figura\(\PageIndex{4}\). Compare esta curva con la curva generada por la ecuación de Shockley para BJT, Figura 7.2.1. La gráfica se muestra en forma normalizada. En lugar de trazar para valores específicos de\(V_{GS(off)}\) y\(I_{DSS}\), los ejes se presentan como porciones fraccionarias de los máximos (es decir, el eje horizontal es\(−V_{GS}/V_{GS(off)}\) y el eje vertical es\(I_D/I_{DSS}\)).

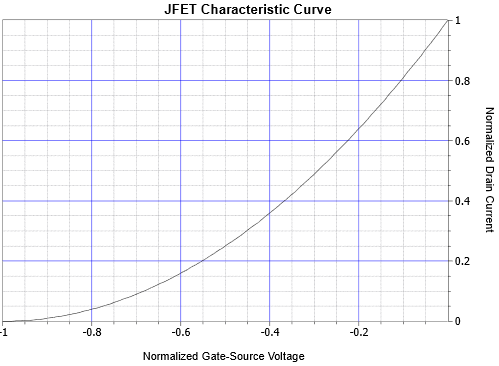
Figura\(\PageIndex{4}\): Curva característica normalizada JFET (nota: esto utiliza\(-V_{GS}/V_{GS(off)}\) para el voltaje normalizado para que la curva no aparezca invertida en comparación con una curva típica de dispositivo).

Ejemplo\(\PageIndex{1}\)

Usando la Ecuación\ ref {10.1} y el gráfico de la Figura\(\PageIndex{4}\), determine la corriente de drenaje si el voltaje puerta-fuente es −1 V y las especificaciones JFET son\(I_{DSS}\) = 8 mA y\(V_{GS(off)}\) = −2 V.

Primero, usando la ecuación\ ref {10.1}

\[I_D = I_{DSS} \left( 1 − \frac{V_{GS}}{V_{GS (off )}} \right)^2 \nonumber \]

\[I_D = 8mA \left( 1 − \frac{−1V}{−2V} \right)^2 \nonumber \]

\[I_D = 2 mA \nonumber \]

Usando la gráfica,\(V_{GS}/V_{GS(off)}\) es 1 V/−2 V, o −0.5. Encuentra este valor en el eje horizontal, sigue a la curva y luego a través del eje vertical derecho. La corriente de drenaje normalizada es 0.25, por lo tanto\(I_D\) es 0.25\(I_{DSS}\), o 2 mA.

Como la curva característica traza la corriente de salida frente al voltaje de entrada, la pendiente de ésta representa la transconductancia, una característica importante para la polarización y el análisis de señales. La transconductancia del dispositivo se denota como\(g_m\), o alternativamente como\(g_{fs}\), y dadas unidades de siemens. Podemos derivar una ecuación para la transconductancia tomando la derivada de la Ecuación\ ref {10.1}.

\[I_D = I_{DSS} \left( 1 − \frac{V_{GS}}{V_{GS (off )}} \right)^2 \nonumber \]

\[\frac{d I_D}{d V_{GS}} =− \frac{2 I_{DSS}}{V_{GS (off )}} \left( 1 − \frac{V_{GS}}{V_{GS (off )}} \right) \nonumber \]

El coeficiente\(−2 I_{DSS}/V_{GS(off)}\) se define como\(g_{m0}\), la transconductancia cuando\(V_{GS} = 0\) V. Esta es la transconductancia máxima del dispositivo. Sustituyendo, llegamos a

\[g_{m0} =− \frac{2 I_{DSS}}{V_{GS(off )}} \label{10.2} \]

\[g_m = g_{m0} \left( 1 − \frac{V_{GS}}{V_{GS (off )}} \right) \label{10.3} \]

En la Figura se muestra una gráfica normalizada de transconductancia versus\(V_{GS}\)\(\PageIndex{5}\). El eje horizontal es\(−V_{GS}/V_{GS(off)}\) y el eje vertical es\(g_m/g_{m0}\).

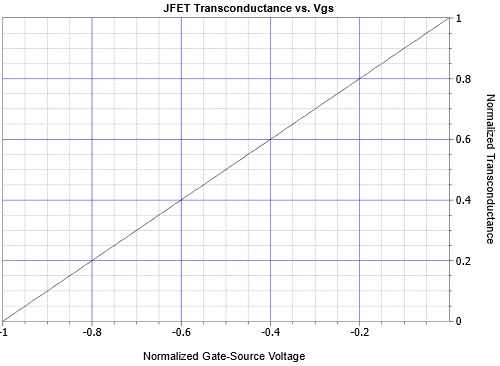
Figura\(\PageIndex{5}\): Curva de transconductancia.

De esta gráfica vemos que la transconductancia es una función lineal.

Otro ítem de interés respecto a estas ecuaciones de dispositivo: Si combinamos las Ecuaciones\ ref {10.1} y\ ref {10.3}, generamos dos ecuaciones que resultarán útiles en el próximo trabajo.

\[\frac{g_m}{g_{m0}} = \sqrt{\frac{I_D}{I_{DSS}}} \label{10.4} \]

\[\frac{I_D}{I_{DSS}} = \left( \frac{g_m}{g_{m0}} \right)^2 \label{10.5} \]

Antes de continuar, los símbolos esquemáticos para los JFET se muestran en la Figura\(\PageIndex{6}\). La línea vertical media representa el canal, y como suele ser el caso, la flecha apunta a N material. A veces la flecha de la puerta se dibuja en el medio en lugar de hacia la fuente. También, como es el caso del BJT, a veces estos símbolos se dibujan dentro de un círculo.

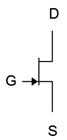
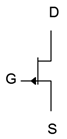
Figura\(\PageIndex{6}\): Símbolos esquemáticos JFET: Canal N (izquierda) Canal P (derecha)

Referencias

¹ Como se evidencia en la ecuación de Shockley, Ecuación 2.1.1.