11.2: Modelo AC simplificado del JFET

Última actualización
Guardar como PDF

Page ID: 83460

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

En la Figura se muestra un modelo AC del JFET\(\PageIndex{1}\). Este es esencialmente el mismo modelo que se utilizó para el análisis de DC. Una vez más, tenemos una fuente de corriente controlada por voltaje situada en el desagüe. La unión con sesgo inverso se presenta como una resistencia muy grande,\(r_{GS}\).

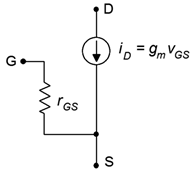
Figura\(\PageIndex{1}\): Modelo AC de JFET.

Cabe mencionar que este modelo es adecuado sólo para bajas frecuencias. A frecuencias más altas, las capacitancias del dispositivo pueden desempeñar un papel importante en la respuesta del amplificador. Hay tres capacitancias de dispositivo no mostradas en la Figura que derivan cada par de terminales:\(C_{GS}\),\(C_{DG}\) y\(C_{DS}\). En una hoja de datos, a menudo se dan las capacitancias “agrupadas”. Estos son\(C_{iss}\), la capacitancia que mira al interior de la puerta con la fuente y el drenaje cortocircuitados a tierra:\(C_{iss} = C_{GS} + C_{DG}\); y\(C_{rss}\), la capacitancia vista desde el desagüe con la puerta y la fuente cortocircuitados a tierra:\(C_{rss} = C_{DS} + C_{DG}\). Como veremos, estas capacitancias pueden tener un impacto considerable en características del amplificador como\(Z_{in}\).

El valor de la transconductancia\(g_m\),, demostrará ser de particular interés. Es más o menos de igual importancia que\(r'_e\) en un BJT. ¹

Referencias

¹ De hecho, podemos decir que\(1/r'_e\) es\(g_m\) para un BJT.