11.5: Circuitos multietapa y combinados

Última actualización
Guardar como PDF

Page ID: 83466

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Las reglas para los circuitos de etapas múltiples que utilizan JFET son las mismas que las discutidas para los BJT: Se deben tomar medidas para garantizar que la polarización de una etapa no afecte negativamente a la polarización de las etapas circundantes (generalmente mediante el uso de condensadores de acoplamiento o yendo a un sistema acoplado de CC), la carga para una etapa dada sea la impedancia de entrada de la siguiente etapa, la impedancia de entrada del sistema será la impedancia de entrada de la primera etapa, y la ganancia del sistema será el producto de las ganancias de etapa individuales.

Teniendo en cuenta esos elementos, no hay límites en cuanto a mezclar BJT con JFET, o mezclar canales N con dispositivos de canal P. Hay ciertas cuestiones prácticas, sin embargo, que podrían dictar dónde se utilizan ciertos dispositivos. Los JFET, debido a su alta impedancia de entrada y su modesto potencial de ganancia, tienden a usarse en la parte frontal de los sistemas de amplificación. Su relativamente bajo ruido propio también es una ventaja en esta ubicación. Los BJT, por otro lado, tienen un alto potencial de ganancia y tienden a ser utilizados en las etapas restantes. Su alta distorsión se puede domar a través del pantano.

Para examinar las posibilidades, recorremos el amplificador mixto y multietapa que se presenta en la Figura\(\PageIndex{1}\).

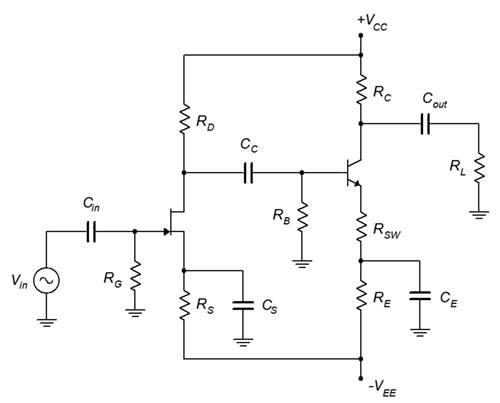
Figura\(\PageIndex{1}\): Amplificador JFET/BJT de dos etapas.

Este amplificador utiliza una fuente de alimentación bipolar que le da al diseñador mucha flexibilidad. La primera etapa consiste en un amplificador de fuente común JFET. Utiliza sesgo combinado (aviso que\(R_S\) está conectado al suministro negativo compartido,\(V_{EE}\), que también sirve como\(V_{SS}\)). \(C_S\)pasa por alto la resistencia de origen para que esta etapa no utilice el pantano. La distorsión no debería ser un problema a menos que la señal de entrada sea bastante grande. La carga para esta etapa está\(R_D\) en paralelo con la impedancia de entrada a la segunda etapa (el condensador de acoplamiento\(C_C\) aparecerá idealmente como un cortocircuito para frecuencias de señal).

La segunda etapa utiliza un BJT NPN configurado como un amplificador de emisor común inundado. Utiliza polarización de emisor de dos fuentes. Su impedancia de entrada es la combinación paralela de\(R_B\) y\(Z_{in(base)}\). La impedancia de entrada base, a su vez, es una función de\(\beta\) y\(R_{SW}\) (solo\(r'_e\) tendrá un pequeño impacto debido a la resistencia de pantano). La carga para esta etapa estará\(R_L\) en paralelo con\(R_C\). Ese valor dividido por le\(R_{SW}\) dará la ganancia aproximada de etapa (nuevamente,\(r'_e\) tendrá poco impacto). Aunque la segunda etapa estará tratando con una señal más grande, la distorsión será mitigada por la resistencia de pantano.

La ganancia del sistema será producto de las ganancias de dos etapas. Como ambos invirtieron la señal, la inversión de la inversión conducirá a una señal de salida que está en fase con la señal de entrada. La impedancia de entrada del sistema dependerá de la primera etapa JFET y se puede aproximar para que sea igual a\(R_G\), al menos a bajas frecuencias.