12.3: Biasing de DE-MOSFET

Última actualización
Guardar como PDF

Page ID: 83379

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Como las ecuaciones características del JFET y DE-MOSFET son las mismas, el modelo de polarización de CC es el mismo. En consecuencia, el DE-MOSFET puede sesgarse usando cualquiera de las técnicas utilizadas con el JFET, incluyendo autopolarización, polarización combinada y polarización de fuente de corriente, ya que estos son todos esquemas de polarización del segundo cuadrante (es decir, tienen un negativo\(V_{GS}\)). Las ecuaciones y gráficas de autosesgo y de sesgo combinado del Capítulo 10 pueden usarse sin modificación. El DE-MOSFET también permite la operación del primer cuadrante, por lo que están disponibles un par de nuevas formas de polarización: polarización cero y polarización del divisor de voltaje. En realidad, ambas son variaciones en la polarización de voltaje constante pero que utilizan el primer cuadrante.

12.3.1: Sesgo Cero

El sesgo cero es único. De alguna manera se puede considerar como un cruce entre la autopolarización y la polarización de voltaje constante. Al igual que la autopolarización, no requiere una segunda fuente de CC para la puerta o el terminal de fuente. Al igual que la polarización de voltaje constante, no hay necesidad de una resistencia de fuente,\(R_S\). En la Figura se muestra un prototipo de polarización cero\(\PageIndex{1}\). No cabe duda de que se trata de un circuito mínimo de recuento de piezas.

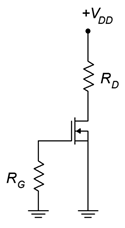
Figura\(\PageIndex{1}\): Prototipo de sesgo cero.

El sesgo cero se llama así porque opera en\(V_{GS} = 0\) V. Recordemos que la corriente de la puerta es idealmente cero, por lo tanto no hay caída a través\(R_G\) y\(V_G = 0\) V como consecuencia. La fuente está atada directamente a tierra, por lo tanto\(V_{GS}\) debe ser igual a 0 V. Como\(V_{GS}\) no cambia, esto puede pensarse como una forma de polarización de voltaje constante. El bit interesante es que cuando se aplica una señal de CA a la puerta, su porción negativa arrastrará el MOSFET hacia abajo al modo de agotamiento y la porción positiva empujará la operación al modo de mejora. Debido a que el dispositivo puede funcionar de esta manera, conduciendo corriente mientras se encuentra a horcajadas en cero, por así decirlo, a los desMOSFET a veces se les conoce como normalmente en los dispositivos.

Determinar el punto de operación para el sesgo cero es sorprendentemente fácil. Porque\(V_{GS} = 0\) V,\(I_D\) debe ser igual\(I_{DSS}\) y\(g_m\) debe igualar\(g_{m0}\). Sin embargo, como todos los esquemas de polarización de voltaje constante, la estabilidad del punto Q no es muy buena. Otro punto a notar es que, como no hay resistencia de fuente, esta polarización solo es aplicable a amplificadores de fuente comunes no inundados. No se puede usar con un seguidor de fuente o amplificador inundado (si se inserta una pequeña resistencia de pantano en la fuente, técnicamente el circuito puede clasificarse como autopolarización, aunque la señal de CA aún puede empujar la operación al modo de mejora).

Ejemplo\(\PageIndex{1}\)

Determine\(I_D\),\(V_D\) y\(g_{m0}\) para el circuito que se muestra en la Figura\(\PageIndex{2}\). Supongamos\(I_{DSS} = 12\) mA y\(V_{GS(off)} = −3\) V.

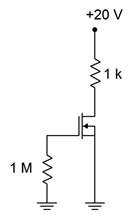
Figura\(\PageIndex{2}\): Circuito por Ejemplo\(\PageIndex{1}\).

Por inspección, ya que esto es sesgo cero\(I_D = I_{DSS}\), y por lo tanto\(I_D = 12\) mA. Usando KVL y la ley de Ohm podemos encontrar\(V_D\).

\[V_D = V_{DD} −I_D R_D \nonumber \]

\[V_D = 20 V−12 mA \times 1k \Omega \nonumber \]

\[V_D = 8 V \nonumber \]

\[g_{m0} =− \frac{2 I_{DSS}}{V_{GS (off )}} \nonumber \]

\[g_{m0} =− \frac{2 \times 12mA}{−3V} \nonumber \]

\[g_{m0} = 8mS \nonumber \]

12.3.2: Bias del divisor de voltaje

La polarización del divisor de voltaje es una forma de polarización de voltaje constante que opera en modo de mejora. Un circuito prototipo se muestra en la Figura\(\PageIndex{3}\). Tenga en cuenta que el terminal de origen está conectado directamente a tierra. Esto es importante. Si este no fuera el caso, esto sería una forma de polarización combinada (básicamente desplazando el\(V_{SS}\) suministro a tierra y luego cambiando el voltaje de la puerta de tierra a un positivo\(V_{SS}\) para mantener el mismo voltaje diferencial). Como tal, estaría operando en modo de agotamiento.

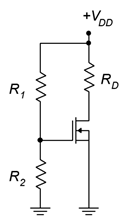
Figura\(\PageIndex{3}\): Prototipo de polarización divisor de voltaje.

El divisor de voltaje comprende\(R_1\) y\(R_2\) establecerá un potencial de polarización de CC en la puerta. Como la fuente está en tierra,\(V_{GS} = V_G = V_{R2}\). Dado que\(V_{DD}\) debe ser positivo, entonces\(V_{GS}\) debe ser positivo, y la operación del modo de mejora es un hecho.

La forma más directa de manejar esto es determinar el potencial del divisor de voltaje y usar la ecuación característica (Ecuación 10.2.1) o gráfica asociada para determinar la corriente de drenaje. Una vez que\(I_D\) se encuentra, el voltaje drenaje-fuente se puede encontrar a través de la ruta estándar de Ohm Law/KVL.

Antes de continuar, tenga en cuenta que los valores de las resistencias divisoras pueden ser muy altos sin crear problemas de polarización (a diferencia de la versión BJT de polarización del divisor de voltaje). Esto se debe a que la corriente de puerta es tan pequeña que incluso cuando se utilizan valores de megohm para el divisor, la carga causada por la puerta no se notará.

Ejemplo\(\PageIndex{2}\)

Para el circuito de la Figura\(\PageIndex{4}\), determinar\(I_D\) y\(V_D\). Supongamos\(I_{DSS} = 2\) mA y\(V_{GS(off)} = −6\) V.

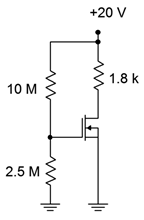
Figura\(\PageIndex{4}\): Circuito por Ejemplo\(\PageIndex{2}\).

El divisor de voltaje cederá\(V_{GS}\).

\[V_{GS} = V_{DD} \left( \frac{R_2}{R_1+R_2} \right) \nonumber \]

\[V_{GS} = 20 V \left( \frac{2.5M \Omega}{ 10 M \Omega +2.5M \Omega} \right) \nonumber \]

\[V_{GS} = 4 V \nonumber \]

Usa la Ecuación 10.2.1 para encontrar\(I_D\).

\[I_D = I_{DSS} \left( 1 − \frac{V_{GS}}{V_{GS (off )}} \right)^2 \nonumber \]

\[I_D = 2 mA \left( 1 − \frac{4V}{−6V} \right)^2 \nonumber \]

\[I_D = 5.56 mA \nonumber \]

Usa la ley de KVL y Ohm para encontrar\(V_D\).

\[V_D = V_{DD} −I_D R_D \nonumber \]

\[V_D = 20 V−5.56 mA \times 1.8k \Omega \nonumber \]

\[V_D = 9.99 V \nonumber \]

Como alternativa, usando la curva de la Figura 12.2.3, encontraríamos primero el voltaje puerta-fuente normalizado que es de 4 V/6 V o 0.667 (tenga en cuenta que la curva grafica\(−V_{GS}/V_{GS(off)}\) para que los cuadrantes no aparezcan invertidos). A partir de esto\(I_D/I_{DSS}\), se puede determinar que la corriente de drenaje normalizada,, es aproximadamente 2.8, dando una corriente de drenaje de 5.6 mA.