2.2: Fuerza magnética en un cable portador de corriente
- Page ID
- 83746
Considere un cable infinitesimalmente delgado y perfectamente conductor que lleve una corriente\(I\) (unidades base SI de A) en el espacio libre. \({\bf B}\left({\bf r}\right)\)Sea la densidad de flujo magnético impresionado en cada punto\({\bf r}\) de la región del espacio ocupado por el cable. Por impresionado, queremos decir que el campo existe en ausencia del cable portador de corriente, a diferencia del campo que es inducido por esta corriente. Dado que la corriente consiste en partículas cargadas en movimiento,\({\bf B}({\bf r})\) esperamos que ejerza una fuerza sobre la corriente. Dado que la corriente está restringida para fluir en el cable, esperamos que esta fuerza también sea experimentada por el cable. Consideremos ahora esta fuerza.
Para comenzar, recordemos que la fuerza ejercida sobre una carga portadora de partículas\(q\) que tiene velocidad\({\bf v}\) es
\[{\bf F}_m\left({\bf r}\right) = q{\bf v}\left({\bf r}\right) \times {\bf B}\left({\bf r}\right) \nonumber \]
Así, la fuerza ejercida sobre una cantidad diferencial de carga\(dq\) es
\[d{\bf F}_m\left({\bf r}\right) = dq~{\bf v}\left({\bf r}\right) \times {\bf B}\left({\bf r}\right) \nonumber \]
Let\(d{\bf l}\left({\bf r}\right)\) representa un segmento de longitud diferencial del cable en\({\bf r}\), apuntando en la dirección del flujo de corriente. Entonces
\[dq~{\bf v}\left({\bf r}\right) = I d{\bf l}\left({\bf r}\right) \nonumber \]
(Si esto no está claro, podría ayudar considerar las unidades: A la izquierda, C\(\cdot\) m/s\(=\) (C/s)\(\cdot\) m\(=\) A\(\cdot\) m, como a la derecha.) Posteriormente,
\[d{\bf F}_m\left({\bf r}\right) = I d{\bf l}\left({\bf r}\right) \times {\bf B}\left({\bf r}\right) \label{m0017_edmforce} \]
Hay tres casos importantes de interés práctico. Primero, considere un segmento recto\({\bf l}\) que forma parte de un bucle cerrado de corriente en una densidad de flujo magnético impresionado espacialmente uniforme\({\bf B}\left({\bf r}\right)={\bf B}_0\). En este caso, la fuerza ejercida por el campo magnético sobre dicho segmento viene dada por la Ecuación\ ref {m0017_edmforce} con\(d{\bf l}\) reemplazada por\({\bf l}\); es decir:
\[\boxed{ {\bf F}_m = I {\bf l} \times {\bf B}_0 } \label{m0017_emforce} \]
Resumiendo,
La fuerza experimentada por un segmento recto de alambre portador de corriente en un campo magnético espacialmente uniforme viene dada por la Ecuación\ ref {m0017_emforce}.
El segundo caso de interés práctico es un bucle cerrado rígido de corriente en una densidad de flujo magnético espacialmente uniforme\({\bf B}_0\). Si el bucle consiste en lados rectos, por ejemplo, un bucle rectangular, entonces la fuerza aplicada al bucle es la suma de las fuerzas aplicadas a cada lado por separado, según lo determinado por la Ecuación\ ref {m0017_emforce}. Sin embargo, deseamos considerar bucles de forma arbitraria. Para acomodar bucles de forma arbitraria, deja\(\mathcal{C}\) ser el camino a través del espacio ocupado por el bucle. Entonces la fuerza experimentada por el bucle es
\[\begin{aligned} {\bf F} &= \int_{\mathcal{C}} d{\bf F}_m\left({\bf r}\right) \nonumber \\ &= \int_{\mathcal{C}} I d{\bf l}\left({\bf r}\right) \times {\bf B}_0 \end{aligned} \nonumber \]
Dado que\(I\) y\({\bf B}_0\) son constantes, pueden extraerse de la integral:
\[{\bf F} = I \left[ \int_{\mathcal{C}} d{\bf l}\left({\bf r}\right) \right] \times {\bf B}_0 \nonumber \]
Tenga en cuenta que la cantidad entre corchetes es cero. Por lo tanto:
La fuerza neta en un bucle de cable portador de corriente en un campo magnético uniforme es cero.
Tenga en cuenta que esto no excluye la posibilidad de que el bucle rígido rote; por ejemplo, la fuerza en lados opuestos del bucle puede ser igual y opuesta. Lo que hemos encontrado es meramente que la fuerza no conducirá a una fuerza neta traslacional en el bucle; por ejemplo, una fuerza que impulsaría al bucle lejos de su posición actual en el espacio. La posibilidad de rotación sin traslación conduce al concepto más rudimentario para un motor eléctrico. Los motores eléctricos prácticos utilizan variaciones sobre esencialmente esta misma idea; consulte “Lectura adicional” para obtener más información.
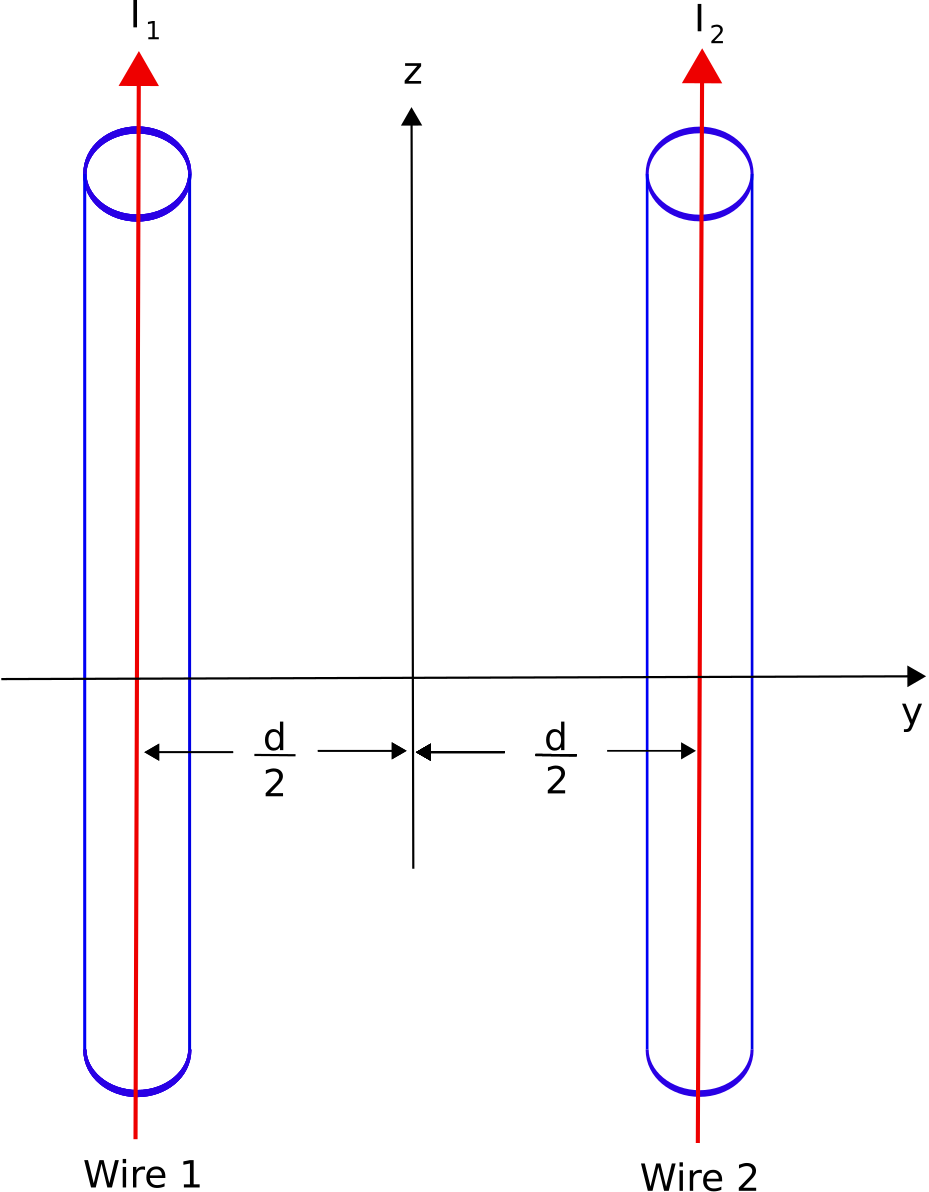
El tercer caso de interés práctico es la fuerza experimentada por dos alambres paralelos infinitesimamente delgados en el espacio libre, como se muestra en la Figura\(\PageIndex{1}\). Aquí los cables son infinitos en longitud (volveremos a eso en un momento), se encuentran en el\(x=0\) plano, están separados por la distancia\(d\), y transportan corrientes\(I_1\) y\(I_2\), respectivamente. La corriente en el cable 1 da lugar a una densidad de flujo magnético\({\bf B}_1\). La fuerza ejercida sobre el alambre 2 por\({\bf B}_1\) es:
\[{\bf F}_2 = \int_{\mathcal{C}} \left[ I_2 d{\bf l}\left({\bf r}\right) \times {\bf B}_1\left({\bf r}\right) \right] \label{m0017_eF2} \]
donde\(\mathcal{C}\) está el camino seguido por\(I_2\), y\(d{\bf l}\left({\bf r}\right)=\hat{\bf z}dz\). Una forma sencilla de determinar\({\bf B}_1\) en esta situación es la siguiente. Primero, si el cable 1 se hubiera alineado a lo largo de la\(x=y=0\) línea, entonces la densidad de flujo magnético en todas partes sería
\[\hat{\bf \phi}\frac{\mu_0 I_1}{2\pi\rho} \nonumber \]
En el presente problema, el cable 1 se desplaza\(d/2\) en la\(-\hat{\bf y}\) dirección. Si bien esto parecería complicar la nueva expresión, tenga en cuenta que las únicas posiciones donde\({\bf B}_1\left({\bf r}\right)\) se requieren valores de son las correspondientes\(\mathcal{C}\); es decir, puntos en el cable 2. Para estos puntos,
\[{\bf B}_1\left({\bf r}\right) = -\hat{\bf x}\frac{\mu_0 I_1}{2\pi d} ~~~ \mbox{along}~\mathcal{C} \nonumber \]
Es decir, la distancia relevante es\(d\) (no\(\rho\)), y la dirección de\({\bf B}_1\left({\bf r}\right)\) para los puntos a lo largo\(\mathcal{C}\) es\(-\hat{\bf x}\) (no\(\hat{\bf \phi}\)). Volviendo a la Ecuación\ ref {M0017_EF2}, obtenemos:
\[\begin{aligned} {\bf F}_2 &= \int_{\mathcal{C}} \left[ I_2~\hat{\bf z}dz \times \left(-\hat{\bf x}\frac{\mu_0 I_1}{2\pi d}\right) \right] \nonumber \\ &= -\hat{\bf y}\frac{\mu_0 I_1 I_2}{2\pi d} ~ \int_{\mathcal{C}} dz\end{aligned} \nonumber \]
La integral restante es simplemente la longitud del cable 2 que deseamos considerar. Por lo tanto, los cables infinitamente largos resultarán en una fuerza infinita. Este no es un resultado muy interesante o útil. Sin embargo, la fuerza por unidad de longitud del alambre es finita, y se obtiene simplemente dejando caer la integral en la ecuación anterior. Obtenemos:
\[\frac{{\bf F}_2}{\Delta l} = -\hat{\bf y}\frac{\mu_0 I_1 I_2}{2\pi d} \nonumber \]
donde\(\Delta l\) se está considerando la longitud de la sección de alambre 2. Tenga en cuenta que cuando las corrientes\(I_1\) y\(I_2\) fluyen en la misma dirección (es decir, tienen el mismo signo), la fuerza magnética ejercida por la corriente en el cable 1 tira del cable 2 hacia el cable 1.
El mismo proceso se puede utilizar para determinar la fuerza magnética\({\bf F}_1\) ejercida por la corriente en el cable 1 sobre el cable 2. El resultado es
\[\frac{{\bf F}_1}{\Delta l} = +\hat{\bf y}\frac{\mu_0 I_1 I_2}{2\pi d} \nonumber \]
Cuando las corrientes\(I_1\) y\(I_2\) fluyen en la misma dirección (es decir, cuando el producto\(I_1 I_2\) es positivo), entonces la fuerza magnética ejercida por la corriente en el cable 2 tira del cable 1 hacia el cable 2.
Ahora podemos resumir los resultados de la siguiente manera:
Si las corrientes en cables paralelos fluyen en la misma dirección, entonces los cables se atraen; mientras que si las corrientes fluyen en direcciones opuestas, entonces los cables se repelen.
También:
La magnitud de la fuerza asociada es\(\mu_0 I_1 I_2/2\pi d\) para cables separados por distancia\(d\) en medios no magnéticos.
Si los cables están fijos en posición y no pueden moverse, estas fuerzas representan la energía almacenada (potencial). Vale la pena señalar que esta es precisamente la energía que almacena un inductor; por ejemplo, los dos segmentos de alambre aquí podrían interpretarse como segmentos en devanados adyacentes de un inductor en forma de bobina.
Cable de alimentación de CC. Un cable de alimentación conecta una batería de 12 V a una carga que exhibe una impedancia de\(10~\Omega\). Los conductores están separados por 3 mm por una camisa aislante de plástico. Estimar la fuerza entre los conductores.
Solución
La corriente que fluye en cada conductor es de 12 V dividida por\(10~\Omega\), que es 1.2 A. En términos de la teoría desarrollada en esta sección,\(I_1=+1.2\) una corriente A fluye desde el terminal positivo de la batería a la carga en un conductor, y\(I_2=-1.2\) una corriente A regresa a la batería en el otro conductor. El cambio de signo indica que las corrientes a cualquier distancia dada de la batería están fluyendo en direcciones opuestas. También de la declaración del problema,\(d=3\) mm y el aislante es presumiblemente no magnético. Suponiendo que los conductores son aproximadamente rectos, la fuerza entre los conductores es
\[\approx \frac{\mu_0 I_1 I_2}{2\pi d} \cong -96.0~\mu\mbox{N} \nonumber \]
con el signo negativo que indica que los cables se repelen.
Obsérvese en el ejemplo anterior que esta fuerza es bastante pequeña, lo que explica por qué no siempre se observa. Sin embargo, esta fuerza se vuelve significativa cuando la corriente es grande o cuando muchos conjuntos de conductores están unidos mecánicamente entre sí (lo que equivale a una corriente neta mayor), como en un motor.
Lectura adicional:
- “Motor eléctrico” en Wikipedia.


