5.1: Ondas Planas a Incidencia Normal en un Límite Plano

Cuando una onda plana encuentra una discontinuidad en los medios, es posible la reflexión desde la discontinuidad y la transmisión al segundo medio. En esta sección, consideramos el escenario ilustrado en la Figura\(\PageIndex{1}\): una onda plana uniforme que normalmente incide en el límite plano entre dos regiones materiales semiinfinitas. Por “normalmente incidente” queremos decir que la dirección de propagación\(\hat{\bf k}\) es perpendicular al límite. Supondremos que los medios son “simples” y sin pérdidas (es decir, el componente imaginario de permitividad\(\epsilon''\) es igual a cero) y por lo tanto los medios están completamente definidos por una permitividad de valor real y una permeabilidad de valor real.

Figura\(\PageIndex{1}\): Una onda plana uniforme que normalmente incide en el límite plano entre dos regiones materiales semiinfinitas. (CC BY-SA 4.0; C. Wang)

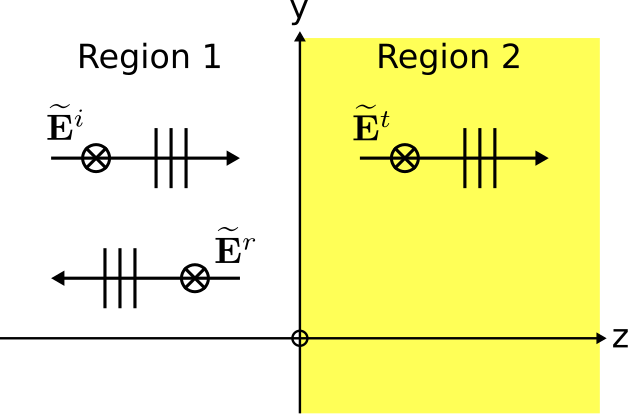
La figura\(\PageIndex{1}\) muestra la onda incidente en el límite, que se encuentra en el\(z=0\) plano. La intensidad del campo eléctrico\(\widetilde{\bf E}^i\) de esta ola viene dada por

\[\widetilde{\bf E}^i(z) = \hat{\bf x} E_0^i e^{-j\beta_1 z}~\mbox{,}~~z \le 0 \label{m0161_eEi} \]

donde\(\beta_1=\omega\sqrt{\mu_1 \epsilon_1}\) es la constante de propagación de fase en la Región 1 y\(E_0^i\) es una constante de valor complejo. \(\widetilde{\bf E}^i\)sirve como el “estímulo” en este problema. Es decir, todas las demás contribuciones al campo total podrán expresarse en términos de\(\widetilde{\bf E}^i\). De hecho, todas las demás contribuciones al campo total pueden expresarse en términos de\(E_0^i\).

A partir de las relaciones de onda plana, determinamos que la intensidad del campo magnético asociado es

\[\widetilde{\bf H}^i(z) = \hat{\bf y} \frac{E_0^i}{\eta_1} e^{-j\beta_1 z}~\mbox{,}~~z \le 0 \label{m0161_eHi} \]

donde\(\eta_1=\sqrt{\mu_1 / \epsilon_1}\) está la impedancia de onda en la Región 1.

La posibilidad de que una onda plana reflejada se propague exactamente en la dirección opuesta se infiere de dos evidencias: La solución general a la ecuación de onda, que incluye términos correspondientes a las ondas que viajan en ambos\(+\hat{\bf z}\) o\(-\hat{\bf z}\); y la simetría geométrica del problema, que impide que las olas viajen en cualquier otra dirección. La simetría del problema también impide un cambio de polarización, por lo que la onda reflejada no debe tener ningún\(\hat{\bf y}\) componente. Por lo tanto, podemos estar seguros de que el campo eléctrico reflejado tiene la forma

\[\widetilde{\bf E}^r(z) = \hat{\bf x} B e^{+j\beta_1 z}~\mbox{,}~~z \le 0 \label{m0161_eEr} \]

donde\(B\) es una constante de valor complejo que queda por determinar. Dado que la dirección de propagación de la onda reflejada es\(-\hat{\bf z}\), tenemos desde las relaciones de onda plana que

\[\widetilde{\bf H}^r(z) = -\hat{\bf y} \frac{B}{\eta_1} e^{+j\beta_1 z}~\mbox{,}~~z \le 0 \label{m0161_eHr} \]

De igual manera, inferimos la existencia de una onda plana “transmitida” que se propaga en el\(z>0\) lado del límite. La simetría del problema excluye cualquier dirección de propagación que no sea\(+{\bf z}\), y sin posibilidad de que una onda viaje en la\(-\hat{\bf z}\) dirección para\(z>0\). Por lo tanto, podemos estar seguros de que el campo eléctrico transmitido tiene la forma:

\[\widetilde{\bf E}^t(z) = \hat{\bf x} C e^{-j\beta_2 z}~\mbox{,}~~z \ge 0 \label{m0161_eEt} \]

y un campo magnético asociado que tiene la forma

\[\widetilde{\bf H}^t(z) = \hat{\bf y} \frac{C}{\eta_2} e^{-j\beta_2 z}~\mbox{,}~~z \ge 0 \label{m0161_eHt} \]

donde\(\beta_2=\omega\sqrt{\mu_2 \epsilon_2}\) y\(\eta_2=\sqrt{\mu_2 / \epsilon_2}\) son la constante de propagación de fase y la impedancia de onda, respectivamente, en la Región 2. La constante\(C\), como\(B\), es una constante de valor complejo que queda por determinar.

En este punto, las únicas incógnitas en este problema son las constantes de valor complejo\(B\) y\(C\). Una vez que se conocen estos valores, el problema queda completamente resuelto. Estos valores se pueden determinar mediante la aplicación de condiciones de contorno en\(z=0\). Primero, recordemos que el componente tangencial de la intensidad total del campo eléctrico debe ser continuo a través de un límite de material. Para aplicar esta condición límite, definamos\(\widetilde{\bf E}_1\) y seamos\(\widetilde{\bf E}_2\) las intensidades totales del campo eléctrico en las Regiones 1 y 2, respectivamente. El campo total en la Región 1 es la suma de campos incidentes y reflejados, por lo que

\[\widetilde{\bf E}_1(z) = \widetilde{\bf E}^i(z) + \widetilde{\bf E}^r(z) \nonumber \]

El campo en la Región 2 es simplemente

\[\widetilde{\bf E}_2(z) = \widetilde{\bf E}^t(z) \nonumber \]

Además, observamos que todos los componentes de campo ya son tangentes al límite. Así, la continuidad del componente tangencial del campo eléctrico a través del límite requiere\(\widetilde{\bf E}_1(0)=\widetilde{\bf E}_2(0)\), y por lo tanto

\[\widetilde{\bf E}^i(0) + \widetilde{\bf E}^r(0) = \widetilde{\bf E}^t(0) %~\mbox{, and} \nonumber \]

Ahora empleando Ecuaciones\ ref {M0161_EEI},\ ref {M0161_EER}, y\ ref {M0161_Eet}, obtenemos:

\[E_0^i + B = C \label{m0161_eBCE} \]

Claramente se requiere una segunda ecuación para determinar ambos\(B\) y\(C\). Esta ecuación se puede obtener aplicando la condición límite en el campo magnético. Recordemos que cualquier discontinuidad en el componente tangencial de la intensidad total del campo magnético debe ser soportada por una corriente que fluye sobre la superficie. No hay corriente impresionada en este problema, y no hay razón para sospechar que surja una corriente en respuesta a los campos presentes en el problema. Por lo tanto, los componentes tangenciales del campo magnético deben ser continuos a través del límite. Esto se convierte en la misma condición límite que aplicamos a la intensidad total del campo eléctrico, por lo que los pasos restantes son los mismos. Definimos\(\widetilde{\bf H}_1\) y\(\widetilde{\bf H}_2\) son las intensidades totales del campo magnético en las Regiones 1 y 2, respectivamente. El campo total en la Región 1 es

\[\widetilde{\bf H}_1(z) = \widetilde{\bf H}^i(z) + \widetilde{\bf H}^r(z) \nonumber \]

El campo en la Región 2 es simplemente

\[\widetilde{\bf H}_2(z) = \widetilde{\bf H}^t(z) \nonumber \]

La condición límite requiere\(\widetilde{\bf H}_1(0)=\widetilde{\bf H}_2(0)\), y por lo tanto

\[\widetilde{\bf H}^i(0) + \widetilde{\bf H}^r(0) = \widetilde{\bf H}^t(0) %~\mbox{, and} \nonumber \]

Ahora empleando ecuaciones\ ref {m0161_ehi}, ref {m0161_ehr}, y\ ref {m0161_eht}, obtenemos:

\[\frac{E_0^i}{\eta_1} - \frac{B}{\eta_1} = \frac{C}{\eta_2} \label{m0161_eBCH} \]

Las ecuaciones\ ref {M0161_EBCE} y\ ref {M0161_EBch} constituyen un sistema lineal de dos ecuaciones simultáneas con dos incógnitas. Un método sencillo de solución es eliminar primero\(C\) sustituyendo el lado izquierdo de la Ecuación\ ref {M0161_EBCE} en la Ecuación\ ref {M0161_EBch}, y luego resolver para\(B\). Se obtiene:

\[B = \Gamma_{12} E_0^i \label{m0161_eB} \]

donde

\[\boxed{ \Gamma_{12} \triangleq \frac{\eta_2-\eta_1}{\eta_2+\eta_1} } \label{m0161_eG} \]

\(\Gamma_{12}\)se conoce como coeficiente de reflexión. El subíndice “12” indica que este coeficiente se aplica para la incidencia de la Región 1 hacia la Región 2. Ahora podemos resolver para\(C\) sustituyendo la Ecuación\ ref {M0161_eb} en la Ecuación\ ref {M0161_EBCE}. Encontramos:

\[C = (1+\Gamma_{12})~E_0^i \nonumber \]

Ahora resumiendo la solución:

\[\boxed{ \widetilde{\bf E}^r(z) = \hat{\bf x} \Gamma_{12} E_0^i e^{+j\beta_1 z} ~~~\mbox{,}~~z \le 0 } \label{m0161_eErf} \]

\[\boxed{ \widetilde{\bf E}^t(z) = \hat{\bf x} \left( 1+\Gamma_{12} \right) E_0^i e^{-j\beta_2 z} ~~~\mbox{,}~~z \ge 0 } \label{m0161_eEtf} \]

Las ecuaciones\ ref {M0161_eERF} y\ ref {M0161_EETF} son los campos reflejados y transmitidos, respectivamente, en respuesta al campo incidente dado en la Ecuación\ ref {M0161_EEI} en el escenario de incidencia normal mostrado en la Figura\(\PageIndex{1}\).

Las expresiones para\(\widetilde{\bf H}^r\) y se\(\widetilde{\bf H}^t\) pueden obtener aplicando las relaciones de onda plana a las expresiones anteriores.

Es útil verificar esta solución examinando algunos casos especiales. Primero: Si el material en la Región 2 es idéntico al material en la Región 1, entonces no debe haber reflexión y\(\widetilde{\bf E}^t=\widetilde{\bf E}^i\). En este caso,\(\eta_2=\eta_1\), así\(\Gamma_{12}=0\), y obtenemos el resultado esperado.

Un segundo caso de interés práctico es cuando la Región 2 es un conductor perfecto. En primer lugar, tenga en cuenta que esto puede parecer a primera vista una violación de la suposición “sin pérdidas” hecha al inicio de esta sección. Si bien es cierto que no dimos cuenta explícitamente de la posibilidad de un conductor perfecto en la Región 2, veamos qué tiene que decir el presente análisis sobre este caso. Si el material en la Región 2 es un conductor perfecto, entonces no debería haber transmisión ya que el campo eléctrico es cero en un conductor perfecto. En este caso,\(\eta_2=0\) ya que la relación entre la intensidad del campo eléctrico y la intensidad del campo magnético es cero en la Región 2, y posteriormente\(\Gamma_{12}=-1\) y\(1+\Gamma_{12}=0\). Como se esperaba,\(\widetilde{\bf E}^t\) se encuentra que es cero, y el campo eléctrico reflejado experimenta un cambio de señal como se requiere para hacer cumplir la condición de límite\(\widetilde{\bf E}^i(0)+\widetilde{\bf E}^r(0)=0\). Así, obtuvimos la respuesta correcta porque pudimos determinarla de manera independiente\(\eta_2=0\) en un conductor perfecto.

Cuando la Región 2 es un conductor perfecto, se aplica el coeficiente de reflexión\(\Gamma_{12}=-1\) y la solución descrita en Ecuaciones\ ref {M0161_eERF} y\ ref {M0161_EETF}.

Puede ser útil observar la muy fuerte analogía entre la reflexión del componente de campo eléctrico de una onda plana desde un límite plano y la reflexión de una onda de voltaje en una línea de transmisión desde una impedancia de terminación. En una línea de transmisión, el coeficiente de reflexión de voltaje\(\Gamma\) viene dado por

\[\Gamma = \frac{Z_L-Z_0}{Z_L+Z_0} \nonumber \]

donde\(Z_L\) es la impedancia de carga y\(Z_0\) es la impedancia característica de la línea de transmisión. Comparando esto con la Ecuación\ ref {M0161_EG}, vemos que\(\eta_1\) es análogo a\(Z_0\) y\(\eta_2\) es análogo a\(Z_L\). Además, vemos que el caso especial\(\eta_2=\eta_1\), considerado anteriormente, es análogo a una carga emparejada, y el caso especial\(\eta_2=0\), también considerado anteriormente, es análogo a una carga de cortocircuito.

En el caso de las líneas de transmisión, nos preocupaba qué fracción de la potencia se entregaba a una carga y qué fracción de la potencia se reflejaba a partir de una carga. Una pregunta similar se aplica en el caso de la reflexión de onda plana. En este caso, nos preocupa qué fracción de la densidad de potencia se transmite a la Región 2 y qué fracción de la densidad de potencia se refleja desde el límite. La densidad de potencia promedio en el tiempo\(S_{ave}^i\) asociada con la onda incidente es:

\[S_{ave}^i = \frac{|E^i_0|^2}{2\eta_1} \nonumber \]

suponiendo que\(E^i_0\) se expresa en unidades pico (a diferencia de rms). De manera similar, la densidad de potencia promedio en el tiempo\(S_{ave}^r\) asociada a la onda reflejada es:

\[\begin{align} S_{ave}^r &= \frac{\left|\Gamma_{12} E_0^i\right|^2}{2\eta_1} \nonumber \\ &= \left|\Gamma_{12}\right|^2 \frac{\left|E_0^i\right|^2}{2\eta_1} \nonumber \\ &= \left|\Gamma_{12}\right|^2 S_{ave}^i \label{m0161_eSaver}\end{align} \]

Desde el principio de conservación de la energía, la densidad de potencia\(S_{ave}^t\) transmitida a la Región 2 debe ser igual a la densidad de potencia incidente menos la densidad de potencia reflejada. Así:

\[\begin{align} S_{ave}^t &= S_{ave}^i - S_{ave}^r \nonumber \\ &= \left( 1-|\Gamma_{12}|^2 \right)S_{ave}^i\end{align} \nonumber \]

En otras palabras, la relación entre la densidad de potencia transmitida a la Región 2 y la densidad de potencia incidente de la Región 1 es

\[\boxed{ \frac{S_{ave}^t}{S_{ave}^i} = 1-|\Gamma_{12}|^2 } \label{m0161_eSavet} \]

Nuevamente, la analogía con la teoría de líneas de transmisión es evidente.

Las fracciones de densidad de potencia reflejadas y transmitidas en relación con la densidad de potencia incidente se dan en términos del coeficiente de reflexión\(\Gamma_{12}\) por las Ecuaciones\ ref {M0161_Esaver} y\ ref {M0161_Esavet}, respectivamente.

Por último, señalar que existe una variedad de expresiones alternativas para el coeficiente de reflexión\(\Gamma_{12}\). Dado que la impedancia de onda\(\eta=\sqrt{\mu/\epsilon}\) en medios sin pérdidas, y dado que la mayoría de los materiales sin pérdidas son no magnéticos (es decir, exhiben\(\mu\approx\mu_0\)), es posible expresar\(\Gamma_{12}\) puramente en términos de permitividad para estos medios. Suponiendo\(\mu=\mu_0\), encontramos:

\[\begin{align} \Gamma_{12} &= \frac{\eta_2-\eta_1}{\eta_2+\eta_1} \nonumber \\ &= \frac{\sqrt{\mu_0/\epsilon_2}-\sqrt{\mu_0/\epsilon_1}}{\sqrt{\mu_0/\epsilon_2}+\sqrt{\mu_0/\epsilon_1}} \nonumber \\ &= \frac{\sqrt{\epsilon_1}-\sqrt{\epsilon_2}}{\sqrt{\epsilon_1}+\sqrt{\epsilon_2}} \end{align} \nonumber \]

Además, recordemos que la permitividad puede expresarse en términos de permitividad relativa; es decir,\(\epsilon=\epsilon_r\epsilon_0\). Haciendo la sustitución anterior y eliminando todos los factores extraños de\(\epsilon_0\), encontramos:

\[\Gamma_{12} = \frac{\sqrt{\epsilon_{r1}}-\sqrt{\epsilon_{r2}}}{\sqrt{\epsilon_{r1}}+\sqrt{\epsilon_{r2}}} \label{m0161_eGer} \]

donde\(\epsilon_{r1}\) y\(\epsilon_{r2}\) son las permitividades relativas en las Regiones 1 y 2, respectivamente.

Ejemplo\(\PageIndex{1}\): Radio reflection from the surface of the Moon

A frecuencias de radio, la Luna se puede modelar como un dieléctrico de baja pérdida con permitividad relativa de aproximadamente 3. Caracterizar la eficiencia del reflejo de una onda de radio de la Luna.

Solución

A frecuencias de radio, una longitud de onda es muchos órdenes de magnitud menor que el diámetro de la Luna, por lo que estamos justificados en tratar la superficie de la Luna como un límite plano entre el espacio libre y una región semi-infinita de material dieléctrico con pérdidas. El coeficiente de reflexión viene dado aproximadamente por la Ecuación\ ref {M0161_Eger} con\(\epsilon_{r1}\approx 1\) y\(\epsilon_{r2}\sim 3\). Así,\(\Gamma_{12}\sim-0.27\). Posteriormente, la fracción de poder reflejada desde la Luna en relación con el incidente de poder es\(\left|\Gamma_{12}\right|^2\sim 0.07\); es decir, alrededor del 7%.

En óptica, es común hacer la definición\(n\triangleq \sqrt{\epsilon_r}\) donde\(n\) se conoce como el índice de refracción o índice de refracción. ¹ En términos de los índices de refracción\(n_1\) y\(n_2\) para las Regiones 1 y 2, respectivamente:

\[\Gamma_{12} = \frac{n_1-n_2}{n_1+n_2} \nonumber \]

Lectura adicional:

• “Índice de refracción” en Wikipedia.

---

1. Un poco inapropiada, ya que la definición se aplica incluso cuando no hay refracción, como en el escenario considerado en esta sección. ↩