5.6: Ondas Planas en Incidencia Oblicua en un Caso de Límite Plano
- Page ID
- 83783
En esta sección, consideramos el problema de la reflexión y transmisión desde un límite plano entre medios semi-infinitos para una onda plana uniforme transversal eléctrica (TE). Antes de intentar esta sección, se recomienda una revisión de las Secciones 5.1 (“Ondas Planas a Incidencia Normal en un Límite Plano entre Medios sin Perdida”) y 5.5 (“Descomposición de una Onda en Componentes TE y TM”). También, tenga en cuenta que esta sección tiene mucho en común con la Sección 5.7 (“Ondas Planas a Incidencia Oblicua en un Límite Plano: Caso TM”), aunque se recomienda intentar primero el caso TE.
El caso TE se ilustra en la Figura\(\PageIndex{1}\).
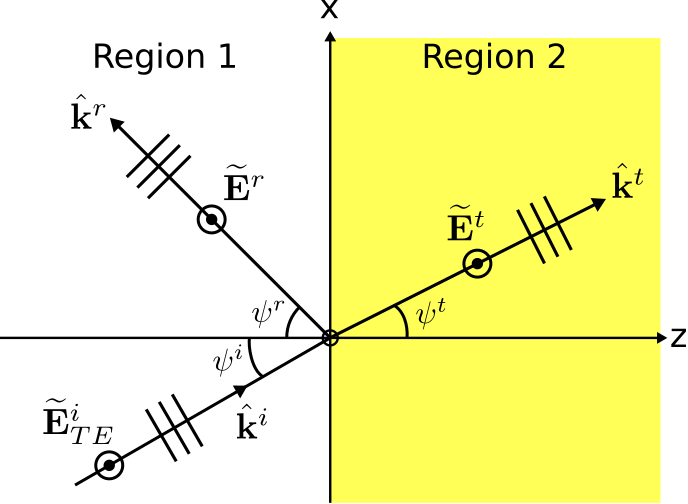
El límite entre las dos regiones semiinfinitas y sin pérdidas se encuentra en el\(z=0\) plano. La ola es incidente de la Región 1. La intensidad del campo eléctrico\(\widetilde{\bf E}^i_{TE}\) de esta ola viene dada por
\[\widetilde{\bf E}^i_{TE}({\bf r}) = \hat{\bf y} E^i_{TE} e^{-j{\bf k}^i\cdot{\bf r}} \label{m0167_eEi} \]
En esta expresión,\({\bf r}\) se encuentra la posición en la que\(\widetilde{\bf E}^i_{TE}\) se evalúa, y
\[{\bf k}^i = \hat{\bf k}^i \beta_1 \nonumber \]
donde\(\hat{\bf k}^i\) es el vector unitario que indica la dirección de propagación y\(\beta_1=\omega\sqrt{\mu_1 \epsilon_1}\) es la constante de propagación de fase en la Región 1. \(\widetilde{\bf E}^i_{TE}\)sirve como el “estímulo” en este problema, por lo que todas las demás contribuciones al campo total se expresarán en términos de cantidades que aparecen en la Ecuación\ ref {M0167_EEI}.
La presencia de ondas planas uniformes reflejadas y transmitidas se deduce de nuestra experiencia con el escenario de incidencia normal (Sección 5.1). Ahí, como aquí, la simetría del problema indica que los componentes reflejados y transmitidos del campo eléctrico tendrán la misma polarización que la del campo eléctrico incidente. Esto se debe a que no hay nada presente en el problema que pueda dar cuenta de un cambio en la polarización. Así, los campos reflejados y transmitidos también serán TE. Por lo tanto, postulamos la siguiente expresión para la onda reflejada:
\[\widetilde{\bf E}^r({\bf r}) = \hat{\bf y} B e^{-j{\bf k}^r\cdot{\bf r}} \label{m0167_eEr} \]
donde\(B\) hay que determinar una constante desconocida, posiblemente de valor complejo y
\[{\bf k}^r = \hat{\bf k}^r \beta_1 \nonumber \]
indica la dirección de propagación, que también se desconoce actualmente.
Del mismo modo, postulamos la siguiente expresión para la onda transmitida:
\[\widetilde{\bf E}^t({\bf r}) = \hat{\bf y} C e^{-j{\bf k}^t\cdot{\bf r}} \label{m0167_eEt} \]
donde\(C\) hay que determinar una constante desconocida, posiblemente de valor complejo;
\[{\bf k}^t = \hat{\bf k}^t \beta_2 \nonumber \]
donde\(\hat{\bf k}^t\) es el vector unitario que indica la dirección de propagación; y\(\beta_2=\omega\sqrt{\mu_2 \epsilon_2}\) es la constante de propagación de fase en la Región 2.
En este punto, las incógnitas en este problema son las constantes\(B\) y\(C\), así como las direcciones\(\hat{\bf k}^r\) y\(\hat{\bf k}^t\). Podemos establecer una relación entre\(E^i_{TE}\),\(B\), y\(C\) mediante la aplicación de condiciones de límite en\(z=0\). Primero, recordemos que el componente tangencial de la intensidad total del campo eléctrico debe ser continuo a través de los límites del material. Para aplicar esta condición límite, definamos\(\widetilde{\bf E}_1\) y seamos\(\widetilde{\bf E}_2\) los campos eléctricos totales en las Regiones 1 y 2, respectivamente. El campo total en la Región 1 es la suma de campos incidentes y reflejados, por lo que
\[\widetilde{\bf E}_1({\bf r}) = \widetilde{\bf E}^i_{TE}({\bf r}) + \widetilde{\bf E}^r({\bf r}) \nonumber \]
El campo total en la Región 2 es simplemente
\[\widetilde{\bf E}_2({\bf r}) = \widetilde{\bf E}^t({\bf r}) \nonumber \]
A continuación, tenga en cuenta que todos los componentes del campo eléctrico ya son tangentes al límite. Así, la continuidad del componente tangencial del campo eléctrico a través del límite requiere\(\widetilde{\bf E}_1(0)=\widetilde{\bf E}_2(0)\), y por lo tanto
\[\widetilde{\bf E}^i_{TE}({\bf r}_0) + \widetilde{\bf E}^r({\bf r}_0) = \widetilde{\bf E}^t({\bf r}_0) \nonumber \]
donde\({\bf r}={\bf r}_0\triangleq\hat{\bf x}x+\hat{\bf y}y\) desde\(z=0\) en el límite. Ahora empleando Ecuaciones\ ref {M0167_EEI},\ ref {M0167_EER}, y\ ref {M0167_EET}, obtenemos:
\[\hat{\bf y}E^i_{TE}e^{-j{\bf k}^i\cdot{\bf r}_0} + \hat{\bf y}B e^{-j{\bf k}^r\cdot{\bf r}_0} = \hat{\bf y}C e^{-j{\bf k}^t\cdot{\bf r}_0} \label{m0167_eBCE} \]
Dejando caer el vector (\(\hat{\bf y}\)) ya que es el mismo en cada término, obtenemos:
\[E^i_{TE}e^{-j{\bf k}^i\cdot{\bf r}_0} + B e^{-j{\bf k}^r\cdot{\bf r}_0} = C e^{-j{\bf k}^t\cdot{\bf r}_0} \label{m0167_eBCE2} \]
Para que la Ecuación\ ref {M0167_EBCE2} sea verdadera\({\bf r}_0\) en cada punto del límite, debe ser cierto que
\[{\bf k}^i\cdot{\bf r}_0 = {\bf k}^r\cdot{\bf r}_0 = {\bf k}^t\cdot{\bf r}_0 \label{m0167_eSL} \]
Esencialmente, estamos requiriendo que las fases de cada campo en las Regiones 1 y 2 se emparejen en cada punto a lo largo del límite. Cualquier otra elección resultará en una violación de las condiciones de los límites en algún momento a lo largo del límite. Este criterio de coincidencia de fases determinará las direcciones de propagación de los campos reflejados y transmitidos, lo que haremos posteriormente.
Primero, utilicemos el criterio de coincidencia de fases para completar la solución para los coeficientes\(B\) y\(C\). Aplicando la Ecuación\ ref {M0167_ESL}, observamos que la Ecuación\ ref {M0167_EBCE2} se reduce a:
\[E^i_{TE} + B = C \label{m0167_eBCE3} \]
Se necesita una segunda ecuación ya que actualmente solo tenemos una ecuación (Ecuación\ ref {M0167_EBCE3}) y dos incógnitas (\(B\)y\(C\)). La segunda ecuación se obtiene aplicando las condiciones de límite apropiadas al campo magnético. El campo magnético asociado con cada uno de los componentes del campo eléctrico se identifica en la Figura\(\PageIndex{2}\).
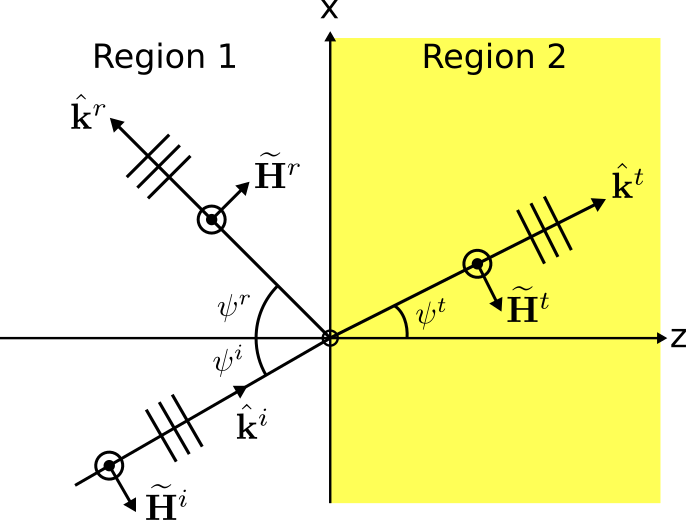
Tenga en cuenta que las orientaciones de los vectores de campo magnético pueden confirmarse usando las relaciones de onda plana: Específicamente, el producto cruzado de los campos eléctrico y magnético debe apuntar en la dirección de propagación. Las expresiones para cada uno de los componentes del campo magnético se determinan formalmente a continuación.
A partir de las relaciones de onda plana, determinamos que la intensidad del campo magnético incidente es
\[\widetilde{\bf H}^i({\bf r}) = \frac{1}{\eta_1} \hat{\bf k}^i \times \widetilde{\bf E}^i_{TE} \label{m0167_eHi} \]
donde\(\eta_1=\sqrt{\mu_1 / \epsilon_1}\) está la impedancia de onda en la Región 1. Para avanzar se requiere que expresemos\(\hat{\bf k}^i\) en el sistema global de coordenadas fijas. Aquí está:
\[\hat{\bf k}^i = \hat{\bf x}\sin\psi^i + \hat{\bf z}\cos\psi^i \nonumber \]
Así:
\[\widetilde{\bf H}^i({\bf r}) = \left( \hat{\bf z}\sin\psi^i - \hat{\bf x}\cos\psi^i \right) \frac{E^i_{TE}}{\eta_1} e^{-j{\bf k}^i\cdot{\bf r}} \label{m0167_eHi2} \]
De igual manera, determinamos que el campo magnético reflejado tiene la forma:
\[\widetilde{\bf H}^r({\bf r}) = \frac{1}{\eta_1} \hat{\bf k}^r \times \widetilde{\bf E}^r \label{m0167_eHr} \]
En el sistema global de coordenadas:
\[\hat{\bf k}^r = \hat{\bf x}\sin\psi^r - \hat{\bf z}\cos\psi^r \label{m0167_ehkr} \]
Así:
\[\widetilde{\bf H}^r({\bf r}) = \left( \hat{\bf z}\sin\psi^r + \hat{\bf x}\cos\psi^r \right) \frac{B}{\eta_1} e^{-j{\bf k}^r\cdot{\bf r}} \label{m0167_eHr2} \]
El campo magnético transmitido tiene la forma:
\[\widetilde{\bf H}^t({\bf r}) = \frac{1}{\eta_2} \hat{\bf k}^t \times \widetilde{\bf E}^t \label{m0167_eHt} \]
En el sistema global de coordenadas:
\[\hat{\bf k}^t = \hat{\bf x}\sin\psi^t + \hat{\bf z}\cos\psi^t \label{m0167_ehkt} \]
Así:
\[\widetilde{\bf H}^t({\bf r}) = \left( \hat{\bf z}\sin\psi^t - \hat{\bf x}\cos\psi^t \right) \frac{C}{\eta_2} e^{-j{\bf k}^t\cdot{\bf r}} \label{m0167_eHt2} \]
El campo magnético total en la Región 1 es la suma de campos incidentes y reflejados, por lo que
\[\widetilde{\bf H}_1({\bf r}) = \widetilde{\bf H}^i({\bf r}) + \widetilde{\bf H}^r({\bf r}) \nonumber \]
El campo magnético en la Región 2 es simplemente
\[\widetilde{\bf H}_2({\bf r}) = \widetilde{\bf H}^t({\bf r}) \nonumber \]
Dado que no hay corriente en el límite, la componente tangencial de la intensidad total del campo magnético debe ser continua a través del límite. Expresado en términos de las cantidades ya establecidas, esta condición límite requiere:
\[\hat{\bf x}\cdot\widetilde{\bf H}^i({\bf r}_0) + \hat{\bf x}\cdot\widetilde{\bf H}^r({\bf r}_0) = \hat{\bf x}\cdot\widetilde{\bf H}^t({\bf r}_0) \nonumber \]
donde “\(\hat{\bf x}\cdot\)” selecciona el componente del campo magnético que es tangente al límite. Evaluando esta expresión, obtenemos:
\[\begin{align} &-\left(\cos\psi^i\right)\frac{E^i_{TE}}{\eta_1}e^{-j{\bf k}^i\cdot{\bf r}_0} \nonumber \\ &+\left(\cos\psi^r\right)\frac{B}{\eta_1}e^{-j{\bf k}^r\cdot{\bf r}_0} \nonumber \\ = &-\left(\cos\psi^t\right)\frac{C}{\eta_2}e^{-j{\bf k}^t\cdot{\bf r}_0} \end{align} \nonumber \]
Ahora empleando la condición de coincidencia de fase expresada en la Ecuación\ ref {M0167_ESL}, encontramos:
\[\begin{align} &-\left(\cos\psi^i\right)\frac{E^i_{TE}}{\eta_1} \nonumber \\ &+\left(\cos\psi^r\right)\frac{B}{\eta_1} \nonumber \\ = &-\left(\cos\psi^t\right)\frac{C}{\eta_2} \label{m0167_eBCH3}\end{align} \]
Las ecuaciones\ ref {M0167_EBCE3} y\ ref {M0167_EBCH3} comprenden un sistema lineal de ecuaciones con incógnitas\(B\) y\(C\). Este sistema de ecuaciones se resuelve fácilmente de la\(B\) siguiente manera. Primero, use la Ecuación\ ref {M0167_EBCE3} para eliminar\(C\) en la Ecuación\ ref {M0167_EBCh3}. El resultado es:
\[\begin{align} &-\left(\cos\psi^i\right)\frac{E^i_{TE}}{\eta_1} \nonumber \\ &+\left(\cos\psi^r\right)\frac{B}{\eta_1} \nonumber \\ = &-\left(\cos\psi^t\right)\frac{E^i_{TE}+B}{\eta_2} \end{align} \nonumber \]
Resolviendo esta ecuación para\(B\), obtenemos:
\[B = \frac{\eta_2\cos\psi^i-\eta_1\cos\psi^t}{\eta_2\cos\psi^r+\eta_1\cos\psi^t} ~ E^i_{TE} \nonumber \]
Podemos expresar este resultado como un coeficiente de reflexión de la siguiente manera:
\[B = \Gamma_{TE} E^i_{TE} \nonumber \]
donde
\[\Gamma_{TE} \triangleq \frac{\eta_2\cos\psi^i-\eta_1\cos\psi^t}{\eta_2\cos\psi^r+\eta_1\cos\psi^t} \label{m0167_eGTE} \]
Cabe señalar que la Ecuación\ ref {M0167_EGTE} se convierte en el coeficiente de reflexión para la incidencia normal (TEM) cuando\(\psi^i=\psi^r=\psi^t=0\), como se esperaba.
Volviendo a la Ecuación\ ref {M0167_EBCE3}, ahora encontramos
\[C = \left(1+\Gamma_{TE}\right) E^i_{TE} \nonumber \]
Resumimos ahora la solución. Dada la intensidad del campo eléctrico TE expresada en la Ecuación\ ref {M0167_EEI}, encontramos:
\[\boxed{ \widetilde{\bf E}^r({\bf r}) = \hat{\bf y}\Gamma_{TE}E^i_{TE}e^{-j{\bf k}^r\cdot {\bf r}} } \nonumber \]
\[\boxed{ \widetilde{\bf E}^t({\bf r}) = \hat{\bf y}\left(1+\Gamma_{TE}\right)E^i_{TE}e^{-j{\bf k}^t\cdot {\bf r}} } \nonumber \]
Esta solución está completa excepto que aún no hemos determinado\(\hat{\bf k}^r\), que ahora está completamente determinada por\(\psi^r\) medio de la Ecuación\ ref {m0167_ehkr}, y\(\hat{\bf k}^t\), que ahora está completamente determinada por\(\psi^t\) vía de la Ecuación\ ref {m0167_ehkt}. Es decir, aún no hemos determinado las direcciones de propagación\(\psi^r\) para la onda reflejada y\(\psi^t\) para la onda transmitida. Sin embargo,\(\psi^r\) y se\(\psi^i\) puede encontrar usando la Ecuación\ ref {M0167_ESL}. Aquí simplemente indicaremos el resultado, y en la Sección 5.8 realizaremos esta parte de la derivación en detalle y con mayor atención a las implicaciones. Uno encuentra:
\[\psi^r = \psi^i \label{m0167_epsir} \]
y
\[\psi^t = \arcsin\left(\frac{\beta_1}{\beta_2}\sin\psi^i\right) \label{m0167_epsit} \]
La ecuación\ ref {m0167_epsir} es el resultado no sorprendente de que el ángulo de reflexión es igual al ángulo de incidencia. La ecuación\ ref {m0167_epsit} — abordar el ángulo de transmisión — es un poco más intrigante. Los lectores astutos pueden notar que hay algo sospechoso en esta ecuación: Parece posible que el argumento de\(\arcsin\) sea mayor que uno. Esta rareza se aborda en la Sección 5.8.
Finalmente, tenga en cuenta que la Ecuación\ ref {m0167_epsir} nos permite eliminar\(\psi^r\) de la Ecuación\ ref {M0167_EGTE}, rindiendo:
\[\boxed{ \Gamma_{TE} = \frac{\eta_2\cos\psi^i-\eta_1\cos\psi^t}{\eta_2\cos\psi^i+\eta_1\cos\psi^t} } \label{m0167_eGTE2} \]
Así, obtenemos lo que quizás sea el hallazgo más importante de esta sección:
El coeficiente de reflexión del campo eléctrico para la incidencia oblicua de TE\(\Gamma_{TE}\),, viene dado por la Ecuación\ ref {M0167_EGTE2}.
El siguiente ejemplo demuestra la utilidad de este resultado.
La figura\(\PageIndex{3}\) ilustra una onda plana TE que incide desde el aire sobre el límite plano con vidrio. El vidrio exhibe una permitividad relativa de 2.1. Determinar la potencia reflejada y transmitida en relación con el incidente de energía en el límite.
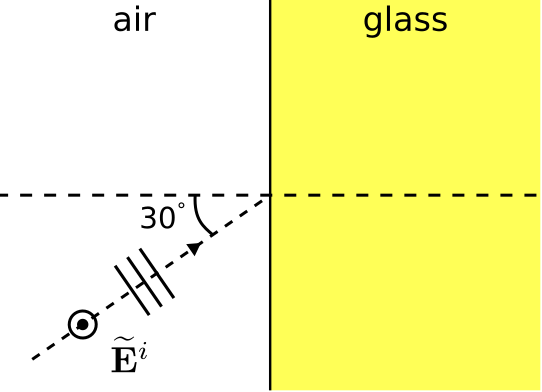
Solución
La potencia reflejada en relación con el incidente de potencia es\(\left|\Gamma_{TE}\right|^2\) mientras que la potencia transmitida en relación con el incidente de potencia es\(1-\left|\Gamma_{TE}\right|^2\). \(\Gamma_{TE}\)puede calcularse usando la Ecuación\ ref {M0167_EGTE2}. Calcular las cantidades que entran en esta expresión:
\[\eta_1 \approx \eta_0 \cong 376.7~\Omega ~~ \mbox{(air)} \nonumber \]
\[\eta_2 \approx \frac{\eta_0}{\sqrt{2.1}} \cong 260.0~\Omega ~~ \mbox{(glass)} \nonumber \]
\[\psi^i = 30^{\circ} \nonumber \]
Nota
\[\frac{\beta_1}{\beta_2} \approx \frac{\omega\sqrt{\mu_0\epsilon_0}}{\omega\sqrt{\mu_0\cdot2.1\epsilon_0}} \cong 0.690 \nonumber \]
por lo
\[\psi^t = \arcsin\left(\frac{\beta_1}{\beta_2}\sin\psi^i\right) \cong 20.2^{\circ} \nonumber \]
Ahora sustituyendo estos valores en la Ecuación\ ref {M0167_EGTE2}, obtenemos
\[\Gamma_{TE} \cong -0.2220 \nonumber \]
Posteriormente, la fracción de poder reflejada en relación con el incidente de potencia es\(\left|\Gamma_{TE}\right|^2\cong 0.049\); es decir, aproximadamente\(4.9\%\). \(1-\left|\Gamma_{TE}\right|^2\cong 95.1\%\)de la potencia se transmite al vidrio.


