5.9: Reflexión TE en medios no magnéticos

La figura\(\PageIndex{1}\) muestra una onda plana uniforme TE incidente en el límite plano entre dos regiones de material semi-infinitas.

Figura\(\PageIndex{1}\): Onda plana uniforme TE que incide oblicuamente en el límite plano entre dos regiones semi-infinitas de material no magnético sin pérdidas (CC BY-SA 4.0; C. Wang)

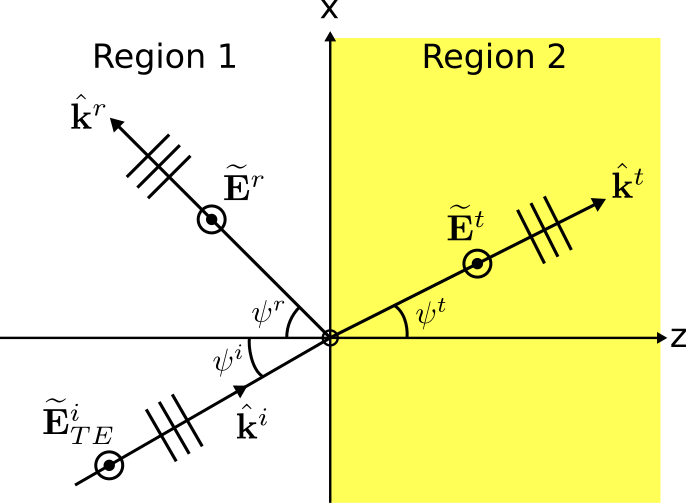
En este caso, el coeficiente de reflexión viene dado por:

\[\Gamma_{TE} = \frac{\eta_2\cos\psi^i-\eta_1\cos\psi^t}{\eta_2\cos\psi^i+\eta_1\cos\psi^t} \label{m0171_eGTE} \]

donde\(\psi^i\) y\(\psi^t\) son los ángulos de incidencia y transmisión (refracción), respectivamente;\(\eta_1\) y\(\eta_2\) son las impedancias de onda en las Regiones 1 y 2, respectivamente. Muchos materiales de interés práctico son no magnéticos; es decir, tienen permeabilidad que no es significativamente diferente de la permeabilidad del espacio libre. En esta sección, consideramos el comportamiento del coeficiente de reflexión para esta clase de materiales.

Para comenzar, recuerda la forma general de la ley de Snell:

\[\sin{\psi^t} = \frac{\beta_1}{\beta_2}\sin\psi^i \label{m0171_eSLNM} \]

En medios no magnéticos, las permeabilidades\(\mu_1\) y\(\mu_2\) se asumen iguales a\(\mu_0\). Así:

\[\frac{\beta_1}{\beta_2} = \frac{\omega\sqrt{\mu_1\epsilon_1}}{\omega\sqrt{\mu_2\epsilon_2}} = \sqrt{\frac{\epsilon_1}{\epsilon_2}} \nonumber \]

Dado que la permitividad se\(\epsilon\) puede expresar como\(\epsilon_0\) veces la permitividad relativa\(\epsilon_r\), podemos reducir aún más a:

\[\frac{\beta_1}{\beta_2} = \sqrt{\frac{\epsilon_{r1}}{\epsilon_{r2}}} \nonumber \]

Ahora la Ecuación\ ref {M0171_ESLNm} se reduce a:

\[\sin{\psi^t} = \sqrt{\frac{\epsilon_{r1}}{\epsilon_{r2}}} \sin\psi^i \nonumber \]

A continuación, tenga en cuenta que para cualquier valor\(\psi\), se puede escribir coseno en términos de seno de la siguiente manera:

\[\cos{\psi} = \sqrt{1-\sin^2{\psi}} \nonumber \]

Por lo tanto,

\[\cos{\psi^t} = \sqrt{1-\frac{\epsilon_{r1}}{\epsilon_{r2}} \sin^2\psi^i } \label{m0171_eCpt} \]

También observamos que en medios no magnéticos

\[\begin{aligned} \eta_1 &= \sqrt{\frac{\mu_1}{\epsilon_1}} = \sqrt{\frac{\mu_0}{\epsilon_{r1}\epsilon_0}} = \frac{\eta_0}{\sqrt{\epsilon_{r1}}} \\ \eta_2 &= \sqrt{\frac{\mu_2}{\epsilon_2}} = \sqrt{\frac{\mu_0}{\epsilon_{r2}\epsilon_0}} = \frac{\eta_0}{\sqrt{\epsilon_{r2}}} \end{aligned} \nonumber \]

donde\(\eta_0\) está la impedancia de onda en el espacio libre. Haciendo sustituciones en la Ecuación\ ref {M0171_EGTE}, obtenemos:

\[\Gamma_{TE} = \frac{\left(\eta_0/\sqrt{\epsilon_{r2}}\right)\cos\psi^i-\left(\eta_0/\sqrt{\epsilon_{r1}}\right)\cos\psi^t}{\left(\eta_0/\sqrt{\epsilon_{r2}}\right)\cos\psi^i+\left(\eta_0/\sqrt{\epsilon_{r1}}\right)\cos\psi^t} \nonumber \]

Multiplicando numerador y denominador por\(\sqrt{\epsilon_{r2}}/\eta_0\), obtenemos:

\[\Gamma_{TE} = \frac{\cos\psi^i-\sqrt{\epsilon_{r2}/\epsilon_{r1}}\cos\psi^t}{\cos\psi^i+\sqrt{\epsilon_{r2}/\epsilon_{r1}}\cos\psi^t} \nonumber \]

Finalmente, sustituyendo la Ecuación\ ref {M0171_Ecpt}, obtenemos:

\[\boxed{ \Gamma_{TE} = \frac{\cos\psi^i-\sqrt{\epsilon_{r2}/\epsilon_{r1}-\sin^2\psi^i}} {\cos\psi^i+\sqrt{\epsilon_{r2}/\epsilon_{r1}-\sin^2\psi^i}} } \label{m0171_eGTEi} \]

Esta expresión tiene la ventaja de que ahora es enteramente en términos de\(\psi^i\), sin necesidad de calcular primero\(\psi^t\).

Usando la ecuación\ ref {M0171_EGTEI}, podemos ver cómo diferentes combinaciones de material afectan el coeficiente de reflexión. Primero, observamos que cuando\(\epsilon_{r1}=\epsilon_{r2}\) (es decir, mismos medios a ambos lados de la frontera),\(\Gamma_{TE}=0\) como se esperaba. Cuando\(\epsilon_{r1}>\epsilon_{r2}\) (por ejemplo, onda viajando en vidrio hacia el aire), vemos que es posible que sea negativo, lo que hace que sea\(\Gamma_{TE}\) de valor complejo.\(\epsilon_{r2}/\epsilon_{r1}-\sin^2\psi^i\) Esto da como resultado una reflexión interna total, y se aborda en otra parte de otra sección. Cuando\(\epsilon_{r1}<\epsilon_{r2}\) (por ejemplo, la ola que viaja en el aire hacia el vidrio), vemos que siempre\(\epsilon_{r2}/\epsilon_{r1}-\sin^2\psi^i\) es positivo, por lo que siempre\(\Gamma_{TE}\) es de valor real.

Sigamos con la\(\epsilon_{r1}<\epsilon_{r2}\) condición. La figura\(\PageIndex{2}\) muestra\(\Gamma_{TE}\) graficamente para diversas combinaciones de medios en todos los ángulos de incidencia posibles de 0 (incidencia normal) a\(\pi/2\) (incidencia de pastoreo).

Figura\(\PageIndex{2}\): El coeficiente\(\Gamma_{TE}\) de reflexión en función del ángulo de incidencia\(\psi^i\) para diversas combinaciones de medios. Las curvas están etiquetadas con la relación\(\epsilon_{r2}/\epsilon_{r1}\).

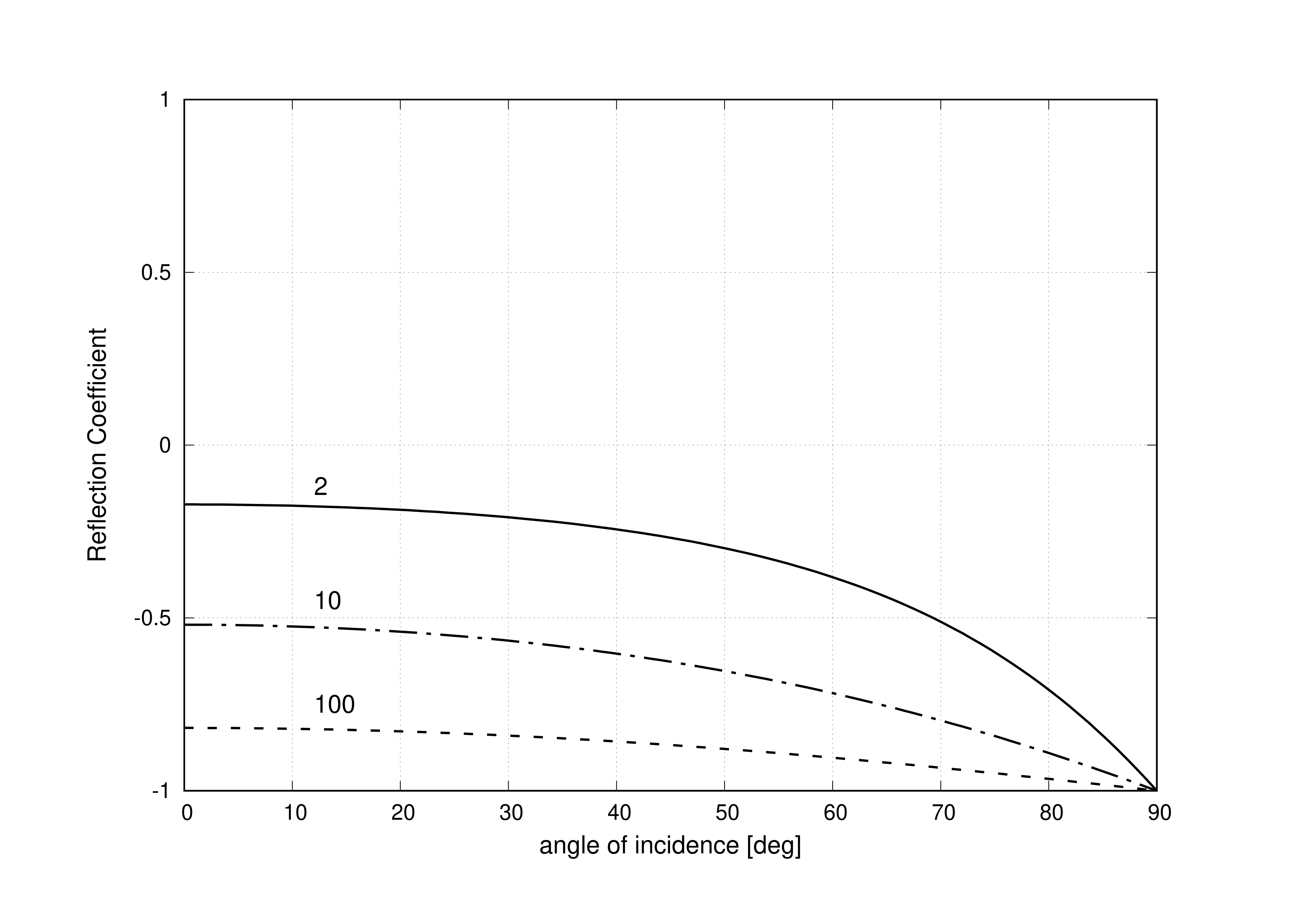
Observamos:

En medios no magnéticos con\(\epsilon_{r1}<\epsilon_{r2}\),\(\Gamma_{TE}\) es de valor real, negativo, y disminuye a\(-1\) medida que se\(\psi^i\) acerca la incidencia de pastoreo.

También tenga en cuenta que en cualquier ángulo particular de incidencia,\(\Gamma_{TE}\) las tendencias hacia\(-1\) como\(\epsilon_{r2}/\epsilon_{r1}\) aumenta. Así, observamos que como\(\epsilon_{r2}/\epsilon_{r1}\to\infty\), el resultado es cada vez más similar al resultado que obtendríamos para un conductor perfecto en la Región 2.