9.3: Solución de la Ecuación de Onda para Potencial de Vector Magnético

El potencial de vector magnético\(\widetilde{\bf A}\) debido a una densidad de corriente\(\widetilde{\bf J}\) viene dado por la siguiente ecuación de onda:

\[\nabla^2 \widetilde{\bf A} -\gamma^2\widetilde{\bf A} = -\mu\widetilde{\bf J} \label{m0196_ePDEA} \]

donde\(\gamma\) está la constante de propagación, definida de la manera habitual ¹

\[\gamma^2\triangleq -\omega^2\mu\epsilon \nonumber \]

La ecuación\ ref {M0196_EPDEA} es una ecuación diferencial parcial que no es homogénea (en el sentido matemático) y puede resolverse dadas las condiciones de límite apropiadas. En esta sección, presentamos la solución para distribuciones arbitrarias de corriente en el espacio libre.

La estrategia es identificar primero una solución para una distribución de corriente que existe en un solo punto. Esta distribución es el momento actual. Un ejemplo de un momento actual se muestra en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Un ejemplo de un momento actual ubicado en el origen. En este caso,\(\hat{\bf{I}}=\hat{\bf{z}}\). (CC BY-SA 4.0; C. Wang)

Una expresión general para un momento actual ubicado en el origen es:

\[\widetilde{\bf J}({\bf r}) = \hat{\bf l}~\widetilde{I}~\Delta l~\delta({\bf r}) \label{m0196_eCM} \]

donde\(\widetilde{I}\) tiene unidades de corriente (unidades base SI de A),\(\Delta l\) tiene unidades de longitud (unidades base SI de m),\(\hat{\bf l}\) es la dirección del flujo de corriente, y\(\delta({\bf r})\) es la función de muestreo volumétrico ² definida de la siguiente manera:

\ begin {align} ~ &\ delta ({\ bf r})\ triangleq 0~~~\ mbox {para} ~~~ {\ bf r}\ neq 0; ~~~\ mbox {y}\ label {m0196_eDelta1}\\ ~ &\ int_ {\ mathcal {V}}\ delta ({\ bf r}) ~dv\ triangleq leq 1\ etiqueta {M0196_Edelta2}\ end {align}

donde\(\mathcal{V}\) está cualquier volumen que incluya el origen (\({\bf r}=0\)). Es evidente a partir de la Ecuación\ ref {M0196_Edelta2} que\(\delta({\bf r})\) tiene unidades base SI de m\(^{-3}\); es decir, volumen inverso. Posteriormente\({\bf J}({\bf r})\) tiene unidades base SI de A/m\(^2\), lo que indica que es una densidad de corriente volumétrica. ³ —como lo indica la Ecuación\ ref {M0196_Edelta1} — existe sólo en el origen y en ninguna otra parte.

Sustituyendo la Ecuación\ ref {M0196_ECM} en la Ecuación\ ref {M0196_EPDEA}, obtenemos:

\[\nabla^2 \widetilde{\bf A} -\gamma^2\widetilde{\bf A} = -\mu\hat{\bf l}~\widetilde{I}~\Delta l~\delta({\bf r}) \label{m0196_ePDEAC} \]

La solución general a esta ecuación que supone medios homogéneos e invariantes en el tiempo (es decir,\(\mu\) y\(\epsilon\) constantes con respecto al espacio y el tiempo) es:

\[\widetilde{\bf A}({\bf r}) = \hat{\bf l}~\mu~\widetilde{I}~\Delta l~\frac{e^{\pm \gamma r}}{4\pi r} \label{m0196_eA} \]

Para confirmar que esta es una solución a la Ecuación\ ref {M0196_EPDEAC}, sustituya esta expresión por la Ecuación\ ref {M0196_EPDEA} y observe que la igualdad se mantiene.

Obsérvese que la Ecuación\ ref {M0196_ea} indica dos soluciones, correspondientes a los signos del exponente en el factor\(e^{\pm \gamma r}\). De hecho, podemos ser un poco más específicos aplicando alguna física de sentido común. Recordemos que\(\gamma\) en general pueden expresarse en términos de componentes reales e imaginarios de la siguiente manera:

\[\gamma = \alpha + j\beta \nonumber \]

donde\(\alpha\) es una constante positiva de valor real conocida como constante de atenuación y\(\beta\) es una constante positiva de valor real conocida como constante de propagación de fase. Por lo tanto, podemos reescribir la Ecuación\ ref {M0196_ea} de la siguiente manera:

\[\widetilde{\bf A}({\bf r}) = \hat{\bf l}~\mu~\widetilde{I}~\Delta l~\frac{ e^{\pm \alpha r} e^{\pm j\beta r} }{4\pi r} \label{m0196_eA2} \]

Consideremos ahora el factor\(e^{\pm \alpha r}/r\), que determina la dependencia de la magnitud de la distancia\(r\). Si elegimos el signo negativo en el exponente, este factor decae exponencialmente al aumentar la distancia desde el origen, llegando finalmente a cero at\(r\rightarrow\infty\). Este es precisamente el comportamiento esperado, ya que esperamos que la magnitud de un campo radiado disminuya al aumentar la distancia desde la fuente. Si por otro lado elegimos el signo positivo en el exponente, este factor aumenta al infinito como\(r\rightarrow\infty\). Ese resultado puede descartarse por motivos físicos, ya que implica la introducción de la energía independientemente de la fuente. El requisito de que la magnitud del campo disminuya a cero a medida que la distancia desde la fuente aumenta hasta el infinito se conoce como la condición de radiación, y es esencialmente una condición límite que se aplica en\(r\rightarrow\infty\). Invocando la condición de radiación, la ecuación\ ref {M0196_ea} se convierte en:

\[\widetilde{\bf A}({\bf r}) = \hat{\bf l}~\mu~\widetilde{I}~\Delta l~\frac{e^{-\gamma r}}{4\pi r} \label{m0196_eA3} \]

En el caso libre de pérdidas (\(\alpha=0\)), no podemos confiar en la condición de radiación para constreñir el signo de\(\gamma\). Sin embargo, en el trabajo de ingeniería práctica siempre hay alguna pérdida de medios; es decir,\(\alpha\) puede ser insignificante pero no es del todo cero. Por lo tanto, normalmente asumimos que la solución para las condiciones sin pérdidas (incluido el espacio libre) viene dada por la Ecuación\ ref {M0196_Ea3} con\(\alpha=0\):

\[\widetilde{\bf A}({\bf r}) = \hat{\bf l}~\mu~\widetilde{I}~\Delta l~\frac{e^{-j \beta r}}{4\pi r} \label{m0196_eA4} \]

Ahora considere el factor\(e^{-j \beta r}\) en la Ecuación\ ref {M0196_EA4}. Este factor determina exclusivamente la dependencia de la fase de\(\widetilde{\bf A}({\bf r})\) al aumentar la distancia\(r\) desde la fuente. En este caso, observamos que las superficies de fase constante corresponden a conchas esféricas que son concéntricas con la fuente. Así,\(\widetilde{\bf A}({\bf r})\) es una onda esférica.

Consideremos ahora una versión un poco más complicada del problema en la que el momento actual ya no se encuentra en el origen, sino que se encuentra en\({\bf r}'\). Esto se ilustra en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Momento actual desplazado del origen. (CC BY-SA 4.0; C. Wang)

Esta distribución de corriente se puede expresar de la siguiente manera:

\[\widetilde{\bf J}({\bf r}) = \hat{\bf l}~\widetilde{I}~\Delta l~\delta({\bf r}-{\bf r}') %\label{m0196_eCM2} \]

La solución en este caso equivale a una modificación directa de la solución existente. Para ver esto, tenga en cuenta que\(\widetilde{\bf A}\) depende sólo de\(r\), y no en absoluto de\(\theta\) o\(\phi\). En otras palabras,\(\widetilde{\bf A}\) depende únicamente de la distancia entre el “punto de campo”\({\bf r}\) en el que observamos\(\widetilde{\bf A}\), y el “punto fuente”\({\bf r}'\) en el que se encuentra el momento actual. Así reemplazamos\(r\) con esta distancia, que es\(\left|{\bf r}-{\bf r}'\right|\). La solución se convierte en:

\[\widetilde{\bf A}({\bf r}) = \hat{\bf l}~\mu~\widetilde{I}~\Delta l~\frac{e^{-\gamma \left|{\bf r}-{\bf r}'\right|}}{4\pi \left|{\bf r}-{\bf r}'\right|} \nonumber \]

Continuando generalizando la solución, consideremos ahora un escenario consistente en un filamento de corriente siguiendo un camino\(\mathcal{C}\) a través del espacio. Esto se ilustra en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Un filamento de corriente que se extiende a lo largo de la trayectoria\(\mathcal{C}\). Esta distribución de corriente puede interpretarse como una colección de momentos actuales que se encuentran a lo largo\(\mathcal{C}\). (CC BY-SA 4.0; C. Wang)

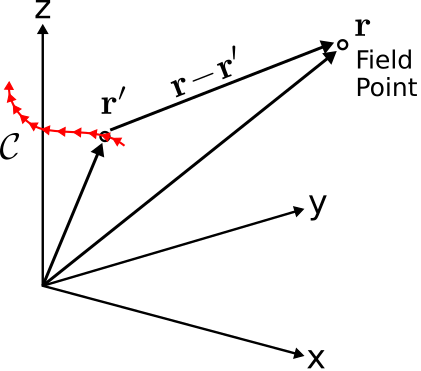
Dicho filamento puede verse como una colección de un gran número de momentos\(N\) de corriente discretos distribuidos a lo largo de la trayectoria. La contribución del momento\(n^{\mbox{th}}\) actual, localizado en\({\bf r}_n\), al potencial total del vector magnético es:

\[\Delta \widetilde{\bf A}({\bf r};{\bf r}_n) = \hat{\bf l}({\bf r}_n)~\mu~\widetilde{I}({\bf r}_n)~\Delta l~\frac{e^{-\gamma \left|{\bf r}-{\bf r}_n\right|}}{4\pi \left|{\bf r}-{\bf r}_n\right|} \nonumber \]

Tenga en cuenta que estamos permitiendo que tanto la dirección actual\(\widetilde{I}\) como la actual varíen con la posición\(\hat{\bf l}\) a lo largo\(\mathcal{C}\). Suponiendo que el medio es lineal, se aplica la superposición. Entonces agregamos estas contribuciones para obtener el potencial total del vector magnético:

\ begin {align}\ Widetilde {\ bf A} ({\ bf r}) &\ approx\ sum_ {n=1} ^ {N}\ Delta\ Widetilde {\ bf A} ({\ bf r}; {\ bf r} _n)\\ &\ approx\ frac {\ mu} {4\ pi} ~\ sum_ {n=1} ^N\ sombrero {\ bf l} ({\ bf r} _n) ~\ Widetilde {I} ({\ bf r} _n) ~\ frac {e^ {-\ gamma\ izquierda| {\ bf r} - {\ bf r} _n\ derecha|}} {\ izquierda| {\ bf r} - {\ bf r} _n\ derecha|} ~\ delta l\ end {align}

Ahora dejando\(\Delta l\rightarrow 0\) para que podamos reemplazar\(\Delta l\) con la longitud diferencial\(dl\):

\[\boxed{ \widetilde{\bf A}({\bf r}) = \frac{\mu}{4\pi}~\int_{\mathcal{C}} \hat{\bf l}({\bf r}')~\widetilde{I}({\bf r}')~\frac{e^{-\gamma \left|{\bf r}-{\bf r}'\right|}}{\left|{\bf r}-{\bf r}'\right|} ~dl } \label{m0196_eAL} \]

donde también hemos reemplazado\({\bf r}_n\) con la notación original\({\bf r}'\) ya que una vez más tenemos un continuo (a diferencia de un conjunto discreto) de ubicaciones de origen.

El potencial de vector magnético correspondiente a la radiación de una distribución lineal de corriente viene dado por la Ecuación\ ref {M0196_eal}.

Dado\(\widetilde{\bf A}({\bf r})\), los campos magnético y eléctrico pueden determinarse utilizando el procedimiento desarrollado en la Sección 9.2.

Lectura adicional:

• “Potencial magnético” en Wikipedia.
• “Función delta Dirac” en Wikipedia.

---

1. Alternativamente,\(\gamma^2\triangleq -\omega^2\mu\epsilon_c\) dar cuenta de la posibilidad de medios con pérdida. ↩
2. También una forma de la función delta de Dirac; ver “Lectura adicional” al final de esta sección. ↩
3. Recuerde, la densidad de una corriente volumétrica es con respecto al área por la que fluye, por lo tanto las unidades son A/m\(^2\). ↩