3.1: Introducción

Una línea de transmisión almacena energía eléctrica y magnética. Como tal línea tiene una forma de circuito que combina inductores,\(L_{s}\) (para la energía magnética), condensadores,\(C_{s}\) (para la energía eléctrica), y resistencias,\(R_{s}\) (pérdidas de modelado), cuyos valores dependen de la geometría de la línea y las propiedades del material.

Las líneas de transmisión consideradas en este capítulo están restringidas a solo dos conductores paralelos, como se muestra en la Figura\(\PageIndex{1}\), siendo la distancia entre los dos hilos (es decir, en la dirección transversal) sustancialmente menor que las longitudes de onda de las señales en la línea. La interpretación física correcta es que los conductores de una línea de transmisión confinan y guían un campo EM. El campo EM contiene la energía de la señal y no la corriente en la línea. Sin embargo, con dimensiones transversales eléctricamente pequeñas, una línea de dos conductores

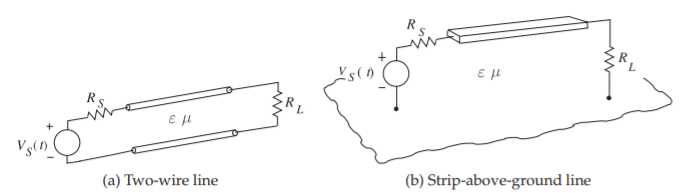
Figura\(\PageIndex{1}\): Líneas de transmisión de dos conductores.

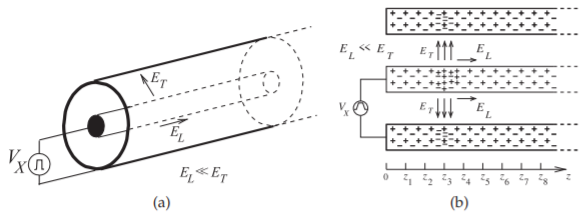
Figura\(\PageIndex{2}\): Una línea de transmisión coaxial: (a) vista tridimensional; (b) la línea con fuente de voltaje pulsado que muestra los campos eléctricos en un instante en el tiempo a medida que un pulso de voltaje viaja por la línea.

pueden analizarse satisfactoriamente sobre la base de voltajes y corrientes.

El análisis de dominio de frecuencia es la mejor manera de entender las líneas de transmisión. Esta teoría de líneas de transmisión con desarrollos modernos se presenta en la Sección 3.2 y se desarrollan fórmulas y conceptos útiles en la Sección 3.3 para líneas de transmisión sin pérdidas. La sección 3.4 presenta varias configuraciones de líneas sin pérdidas que son particularmente útiles en el diseño de circuitos de microondas y utilizadas en muchos lugares de esta serie de libros.

3.1.1 Cuándo debe considerarse una línea de transmisión

El determinante clave de si una línea de transmisión puede considerarse como una conexión invisible entre dos puntos es si la señal en cualquier lugar a lo largo de la interconexión tiene el mismo valor en un instante particular. Si el valor de la señal (digamos, voltaje) varía a lo largo de la línea (en un instante), entonces puede ser necesario considerar los efectos de la línea de transmisión. Un criterio típico utilizado es que si la longitud de la interconexión es menor que la longitud\(1/20\text{th}\) de onda del componente de frecuencia más alta de una señal, entonces los efectos de la línea de transmisión pueden ignorarse de manera segura y el circuito se puede modelar como un solo\(RLC\) circuito [1].

3.1.2 Movimiento de una señal en una línea de transmisión

Cuando se aplica un pulso de voltaje positivo al conductor central de una línea coaxial, como se muestra en la Figura\(\PageIndex{2}\) (a), resulta un campo eléctrico que se dirige desde el conductor central al conductor externo. Haciendo referencia a la Figura\(\PageIndex{2}\) (b), se denota el componente del campo que se dirige a lo largo de la trayectoria más corta desde el conductor central hasta el conductor externo\(E_{T}\), y el subíndice\(T\) denota la componente transversal del campo como se muestra. La figura\(\PageIndex{2}\) (b) muestra los campos en la estructura después de que el pulso haya comenzado a moverse a lo largo de la línea. Esto se muestra en otra vista de la Figura\(\PageIndex{3}\) en cuatro momentos diferentes. El voltaje transversal,\(V_{T}\), viene dado por\(E_{T}\) integrado a lo largo de una trayectoria entre los conductores interno y externo:\(V_{T} ≈ E_{T} (a − b)\). Esta es una buena medida, siempre que las dimensiones transversales sean pequeñas en comparación con una longitud de onda. El pulso de voltaje que excita la línea tiene una forma trapezoidal y el voltaje entre el conductor interno y externo tiene la misma forma que\(E_{T}\). Como indican las ecuaciones de Maxwell, un cambio en el tiempo del campo eléctrico da como resultado un

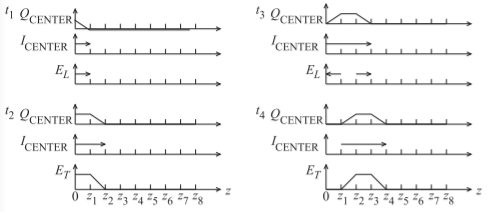
Figura\(\PageIndex{3}\): Campos, corrientes y cargas en la línea de transmisión coaxial de la Figura\(\PageIndex{2}\) a veces\(t_{4} > t_{3} > t_{2} > t_{1}\). \(Q_{\text{CENTER}}\)es el cargo neto gratuito en el conductor central. \(I_{\text{CENTER}}\)es la corriente en el conductor central.

cambio en el campo magnético y por lo tanto la corriente. Como resultado hay una variación de la corriente en el tiempo y esto da como resultado un cambio espacial del campo eléctrico. La búsqueda de una variación de tiempo a una variación espacial y luego de regreso a una variación de tiempo hace que el pulso se mueva hacia abajo en la línea.

El pulso se mueve hacia abajo por la línea a la velocidad del grupo, que para una línea coaxial sin pérdidas es la misma que la velocidad de fase,\(v_{p}\)\(^{1}\). Esto está determinado por las propiedades físicas de la región entre los conductores. La permitividad,\(\varepsilon\), describe el almacenamiento de energía asociado al campo eléctrico\(E\),, y el almacenamiento de energía asociado al campo magnético,\(H\), se describe por la permeabilidad,\(\mu\). Se ha determinado que

\[\label{eq:1}v_{p}=1/\sqrt{\mu\varepsilon} \]

En espacio libre\(v_{p} = c = 1/\sqrt{\mu_{0}\varepsilon_{0}} = 3\times 10^{8}\text{ m/s}\). Las longitudes de onda del espacio libre\(\lambda_{0} = c/f\), a varias frecuencias\(f\), son

\(f\)	\(100\text{ MHz}\)	\(1\text{ GHz}\)	\(10\text{ GHz}\)
\(\lambda_{0}\)	\(3\text{ m}\)	\(30\text{ cm}\)	\(3.0\text{ cm}\)

Mesa\(\PageIndex{1}\)

Ejemplo\(\PageIndex{1}\): Transmission Line Wavelength

Una longitud de línea coaxial se llena con un dieléctrico que tiene una permitividad relativa,\(\varepsilon_{r}\), de\(20\) y está diseñado para ser\(1/4\) longitud de onda larga a una frecuencia,\(f\), de\(1.850\text{ GHz}\). \((\mu_{r} = 1)\)

1. ¿Cuál es la longitud de onda del espacio libre?
2. ¿Cuál es la longitud de onda de la señal en la línea coaxial llena de dieléctrico?
3. ¿Cuánto dura la línea?

Solución

1. \(\lambda_{0}=c/f=3\times 10^{8}/1.85\times 10^{9}=0.162\text{ m}=16.2\text{ cm}\)
2. Tenga en cuenta que para una línea llena de dieléctrico con\(\mu_{r}=1,\:\lambda =v_{p}/f=c/(\sqrt{\varepsilon_{r}}f)=\lambda_{0}/\sqrt{\varepsilon_{r}}\), por lo\(\lambda =\lambda_{0}/\sqrt{\varepsilon_{r}}=16.2\text{ cm}/\sqrt{20}=3.62\text{ cm}\)
3. \(\lambda_{g}/4=3.62\text{ cm}/4=9.05\text{ mm}\)

Notas al pie

[1] La velocidad de fase es la velocidad aparente de un punto de fase constante en una onda sinusoidal y es casi independiente de la frecuencia para una línea coaxial de baja pérdida de pequeñas dimensiones transversales (menores que\(\lambda /10\)).