6.2: Física del Acoplamiento

Si los campos de una línea de transmisión se cruzan con la región alrededor de otra línea de transmisión, entonces parte de la energía que se propaga en la primera línea aparece en la segunda. Este acoplamiento discrimina en términos de ondas que viajan hacia adelante y hacia atrás. En particular, considere las microtiras acopladas que se muestran en la Figura\(\PageIndex{1}\). La dirección de propagación proviene de\(\overline{\mathcal{E}}\times\overline{\mathcal{H}}\). Usando la regla de la derecha, la dirección de propagación de la señal en la franja izquierda está fuera de la página. A esto se le llama la dirección de avance. Ahora considere los campos alrededor de la franja derecha, la línea inactiva, y anote la dirección del\(E\) campo. El\(H\) campo inmediatamente a la izquierda del

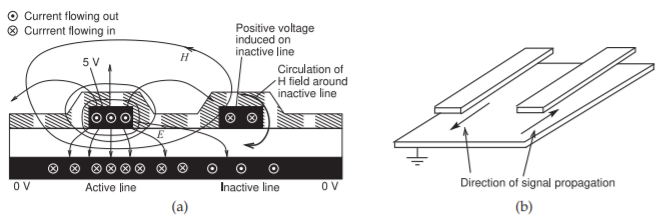
Figura\(\PageIndex{1}\): líneas de microcinta acopladas a bordes con la línea izquierda conducida con el campo de avance que sale de la página: (a) sección transversal de líneas de microcinta tal como se encuentran en una placa de circuito impreso que muestra una capa de pasivación superior conformada o resistencia a la soldadura; y (b) en perspectiva que muestra la dirección de propagación de la línea conducida (izquierda) y la dirección de propagación de la señal acoplada principal en la línea víctima (derecha).

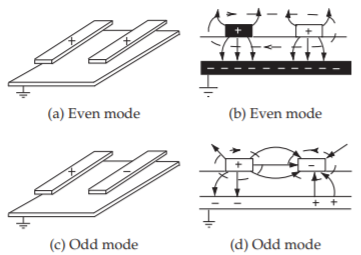
Figura\(\PageIndex{2}\): Modos en líneas de microcinta acopladas en paralelo. En (b) y (d) los campos eléctricos se indican como líneas con flechas y las líneas de campo magnético están discontinuas.

la tira derecha es más fuerte que a la derecha de la tira. Así que efectivamente hay una circulación del\(\mathcal{H}\) campo en el sentido de las agujas del reloj alrededor de la tira derecha. Al aplicar\(\overline{\mathcal{H}}\times\overline{\mathcal{H}}\) a la señal inducida en la tira derecha, se ve que la señal inducida viaja hacia la página, o en la dirección hacia atrás. El acoplamiento con líneas de microcinta acopladas en paralelo se denomina acoplamiento de onda hacia atrás. Tanto el modo par como el modo impar, y ambos tienen componentes de avance y retroceso (ver Figura\(\PageIndex{2}\)).

En el modo par (Figuras\(\PageIndex{2}\) (a y b)), la amplitud y polaridad de las tensiones en los dos conductores de señal son las mismas. En el modo impar (Figuras\(\PageIndex{2}\) (c y d)), los voltajes en los dos conductores de señal son iguales pero tienen polaridad opuesta. Cualquier orientación de campo EM en las líneas acopladas se puede representar como una adición ponderada de las configuraciones de campo de modo par y modo impar. Los campos reales serán una superposición de los modos par e impar. También los voltajes en las líneas están compuestos por componentes pares e impares.

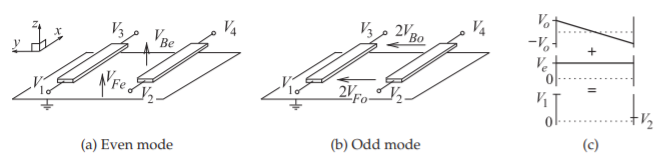
Figura\(\PageIndex{3}\): Definiciones de voltajes totales y fasores de voltaje en modo par e impar en un par de líneas de microcinta acopladas: (a) definición de voltaje en modo par; (b) definición de voltaje en modo impar; (c) representación de cómo se combinan los voltajes de modo par e impar para producir los voltajes totales en líneas individuales. \(F\)indica frente e\(B\) indica atrás.

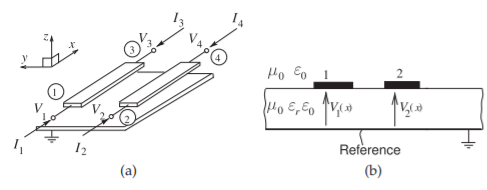
Figura\(\PageIndex{4}\): Líneas de microcinta acopladas: (a) con fasores de voltaje y corriente totales en los cuatro terminales; y (b) sección transversal.

Las impedancias características de los modos par e impar diferirán debido a las diferentes orientaciones de campo. Estas se denominan impedancias características de modo par y modo impar, denotadas por\(Z_{0e}\) y\(Z_{0o}\), respectivamente. Aquí el\(e\) subíndice identifica el modo par y el\(o\) subíndice identifica el modo impar. Con líneas de microcinta acopladas, las velocidades de fase de los dos modos diferirán ya que los dos modos tienen diferentes cantidades de energía en el aire y en el dieléctrico, resultando en diferentes permitividades efectivas de los dos modos.

Las líneas acopladas se modelan determinando las características de propagación de los modos par e impar. Usando las definiciones mostradas en las figuras\(\PageIndex{3}\) y\(\PageIndex{4}\), los fasores de voltaje y corriente totales en la estructura original son una superposición de las soluciones de modo par e impar:

\[\label{eq:1}\left.\begin{array}{ll}{V_{1}=V_{Fe}+V_{Fo}}&{I_{1}=I_{Fe}+I_{Fo}}\\{V_{2}=V_{Fe}-V_{Fo}}&{I_{2}=I_{Fe}-I_{Fo}}\\{V_{3}=V_{Be}+V_{Bo}}&{I_{3}=I_{Be}+I_{Bo}}\\{V_{4}=V_{Be}-V_{Bo}}&{I_{4}=I_{Be}-I_{Bo}}\end{array}\right\} \]

con los subíndices\(F\) e\(B\) indicando la parte delantera y trasera, respectivamente, de los componentes de modo par e impar. También

\[\label{eq:2}\left.\begin{array}{ll}{V_{Fe}=(V_{1}+V_{2})/2}&{I_{Fe}=(I_{1}+I_{2})/2}\\{V_{Fo}=(V_{1}-V_{2})/2}&{I_{Fo}=(I_{1}-I_{2})/2}\\{V_{Be}=(V_{3}+V_{4})/2}&{I_{Be}=(I_{3}+I_{4})/2}\\{V_{Bo}=(V_{3}-V_{4})/2}&{I_{Bo}=(I_{3}-I_{4})/2}\end{array}\right\} \]

Los componentes que viajan hacia adelante se pueden escribir como

\[\label{eq:3}\left.\begin{array}{ll}{V_{1}^{+}=V_{Fe}^{+}+V_{Fo}^{+}}&{I_{1}^{+}=I_{Fe}^{+}+I_{Fo}^{-}}\\{V_{2}^{+}=V_{Fe}^{+}-V_{Fo}^{+}}&{I_{2}^{+}=I_{Fe}^{+}-I_{Fo}^{-}}\\{V_{3}^{+}=V_{Be}^{+}+V_{Bo}^{+}}&{I_{3}^{+}=I_{Be}^{+}+I_{Bo}^{-}}\\{V_{4}^{+}=V_{Be}^{+}-V_{Bo}^{+}}&{I_{4}^{+}=I_{Be}^{+}-I_{Bo}^{-}}\end{array}\right\} \]

Los componentes que viajan hacia atrás se escriben de manera similar para que los voltajes totales de modo par e impar sean

\[\label{eq:4}\left.\begin{array}{ll}{V_{Fe}=V_{Fe}^{+}+V_{Fe}^{-}}&{V_{Be}=V_{Be}^{+}+V_{Be}^{-}}\\{V_{Fo}=V_{Fo}^{+}+V_{Fo}^{-}}&{V_{Bo}=V_{Bo}^{+}+V_{Bo}^{-}}\end{array}\right\} \]

Con un voltímetro ideal los\(V_{4}\) voltajes\(V_{1},\: V_{2},\: V_{3},\) y se medirían desde un punto en la tira hasta un punto en el plano de tierra inmediatamente debajo. Los voltajes\(2V_{Fo}\) y\(2V_{Bo}\) son los voltajes que se medirían entre las tiras en la parte delantera y trasera de las líneas, respectivamente (ver Figura\(\PageIndex{2}\)). No sería posible medir directamente\(V_{Fe}\) y\(V_{Be}\).

Un conjunto de parámetros de red que describen un par de líneas acopladas es la ecuación de matriz de admitancia basada en puertos que relaciona las tensiones de puerto\(V_{1}–V_{4}\),, con las corrientes de puerto,\(I_{1}–I_{4}\):

\[\label{eq:5}\left[\begin{array}{l}{I_{1}}\\{I_{2}}\\{I_{3}}\\{I_{4}}\end{array}\right] =\left[\begin{array}{llll}{y_{11}}&{y_{12}}&{y_{13}}&{y_{14}}\\{y_{21}}&{y_{22}}&{y_{23}}&{y_{24}}\\{y_{31}}&{y_{32}}&{y_{33}}&{y_{34}}\\{y_{41}}&{y_{42}}&{y_{43}}&{y_{44}}\end{array}\right] \left[\begin{array}{l}{V_{1}}\\{V_{2}}\\{V_{3}}\\{V_{4}}\end{array}\right] \]

Estos son\(y\) parámetros basados en puertos, ya que las corrientes y voltajes se definen para los puertos. Dado que las líneas de microcinta se fabrican (la mayor parte del tiempo) en dieléctricos no magnéticos, entonces son recíprocas para que\(y_{ij} = y_{ji}\). El acoplamiento de una línea a otra se describe por los términos\(y_{12} (=y_{21})\) y\(y_{34} (=y_{43})\).

6.2.1 Resumen

El concepto importante introducido en esta sección es que los campos y las ondas propagadoras en un par de líneas acopladas paralelas pueden describirse como una combinación de modos pares e impares, cada uno de los cuales tiene versiones de onda hacia adelante y hacia atrás.