7.5: Parámetros de dispersión y líneas acopladas

Los acopladores direccionales se describieron en la Sección 6.5, pero sin el uso de\(S\) parámetros. Un acoplador direccional con puertos definidos como en la Figura 7-6, y con los puertos emparejados (de modo que\(S_{11} =0= S_{22} = S_{33} = S_{44}\)), tiene la siguiente matriz de parámetros de dispersión:

\[\label{eq:1}\mathbf{S} =\left[\begin{array}{cccc}{0}&{T}&{1/C}&{1/I}\\{T}&{0}&{1/I}&{1/C}\\{1/C}&{1/I}&{0}&{T}\\{1/I}&{1/C}&{T}&{0}\end{array}\right] \]

Hay muchos tipos de acopladores direccionales, y las fases de las olas que viajan en los puertos no necesariamente estarán en fase como\(\eqref{eq:1}\) implica la Ecuación. Cuando la diferencia de fase entre las olas viajeras que entran en el puerto 1 y salen en el puerto 2 es\(90^{\circ}\), la ecuación\(\eqref{eq:1}\) se convierte

\[\label{eq:2}\mathbf{S} =\left[\begin{array}{cccc}{0}&{-\jmath T}&{1/C}&{1/I}\\{-\jmath T}&{0}&{1/I}&{1/C}\\{1/C}&{1/I}&{0}&{-\jmath T}\\{1/I}&{1/C}&{-\jmath T}&{0}\end{array}\right] \]

Ejemplo\(\PageIndex{1}\): Identifying Ports of a Directional Coupler

Un acoplador direccional tiene los siguientes\(S\) parámetros:

\[S=\left[\begin{array}{cccc}{0}&{0.9}&{0.001}&{0.1}\\{0.9}&{0}&{0.1}&{0.001}\\{0.001}&{0.1}&{0}&{0.9}\\{0.1}&{0.001}&{0.9}&{0}\end{array}\right]\nonumber \]

1. ¿Cuáles son los caminos pasantes (es decir, de transmisión)? Identificar dos caminos. Es decir, identificar los pares de puertos en los extremos de los caminos pasantes.
   Primero tenga en cuenta que la asignación de puertos a un acoplador direccional es arbitraria. Por lo que es necesario considerar los\(S\) parámetros para averiguar cómo se relacionan los puertos. Los\(S\) parámetros relacionan las ondas que viajan hacia adelante con las olas que viajan hacia atrás y esto lleva a la comprensión requerida,
   \[\left[\begin{array}{c}{V_{1}^{-}}\\{V_{2}^{-}}\\{V_{3}^{-}}\\{V_{4}^{-}}\end{array}\right] =S\left[\begin{array}{c}{V_{1}^{+}}\\{V_{2}^{+}}\\{V_{3}^{+}}\\{V_{4}^{+}}\end{array}\right] = \left[\begin{array}{cccc}{0}&{0.9}&{0.001}&{0.1}\\{0.9}&{0}&{0.1}&{0.001}\\{0.001}&{0.1}&{0}&{0.9}\\{0.1}&{0.001}&{0.9}&{0}\end{array}\right] \left[\begin{array}{c}{V_{1}^{+}}\\{V_{2}^{+}}\\{V_{3}^{+}}\\{V_{4}^{+}}\end{array}\right]\nonumber \]
   por lo tanto Escribir los parámetros S de esta manera facilita la identificación de las olas que viajan hacia atrás más grandes para cada una de las entradas en los Puertos 1, 2, 3 y 4. La onda que viaja hacia atrás dejará el acoplador direccional y las entradas serán ondas que viajan hacia adelante.
   Considere el Puerto 1, la ola más grande que viaja hacia atrás está en el Puerto 2, y así los Puertos 1 y 2 definen uno de los caminos pasantes. El otro camino pasante es entre los Puertos 3 y 4. Entonces los caminos pasantes son 1—2 y 3—4.
2. ¿Cuál es el puerto acoplado para la señal que ingresa al puerto 1?
   El puerto acoplado es identificado por el puerto con la señal de viaje hacia atrás más grande sin incluir el puerto en el otro extremo de la trayectoria pasante. Para el Puerto 1 el puerto acoplado es el Puerto 4.
3. ¿Cuál es el factor de acoplamiento?
   \[C=\frac{V_{1}^{+}}{V_{4}^{-}}=\frac{1}{0.1}=10=20\text{ dB}\nonumber \]
4. ¿Cuál es el puerto aislado para la señal que ingresa al Puerto 1?
   El puerto aislado es el Puerto 3. La onda que viaja hacia atrás en este puerto es la más pequeña dada una entrada en el Puerto 1.
5. ¿Cuál es el factor de aislamiento?
   \[I=\frac{V_{1}^{+}}{V_{3}^{-}}=\frac{1}{0.001}=1000=60\text{ dB}\nonumber \]
6. ¿Cuál es el factor de directividad?
   El factor de directividad indica cuánto más fuerte es la señal en el puerto acoplado en comparación con el puerto aislado para una señal en la entrada. Para una entrada en el Puerto 1, el factor de directividad es
   \[D=\frac{V_{4}^{-}}{V_{3}^{-}}=\frac{0.1}{0.001}=100=40\text{ dB}\nonumber \]
   Como comprobación\(D = I/C = 1000/10 = 100\).
7. Dibuje un esquema del acoplador direccional.
   Hay cuatro formas de dibujarlo dependiendo del puerto de entrada elegido, ver Figura\(\PageIndex{2}\).

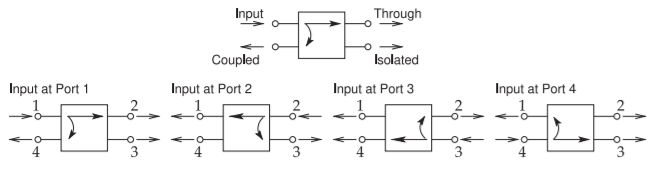
Figura\(\PageIndex{2}\): Esquema del acoplador direccional dibujado con cada uno de los cuatro puertos de entrada posibles.