2.5: Mapas de Karnaugh (K-mapas)

Karnaugh Maps (K-maps) son un mecanismo para crear expresiones booleanas mínimas a partir de una tabla de verdad. Los mapas K se basan en los Códigos Grises para crear el espacio de mapeo, por lo que este capítulo cubrirá primero los Códigos Grises. El capítulo continuará con cómo configurar un mapa K, cómo resolver un mapa K y cómo resolver un mapa K con condiciones de no importa.

\(\PageIndex{1}\)Códigos grises

Los códigos grises son simplemente códigos binarios donde los números adyacentes difieren en un solo dígito. Un número de un solo dígito solo tiene un solo dígito, por lo que es trivial. Ahora considere el Código Gris para números de dos dígitos. Sería:

Tabla\(\PageIndex{1}\): Códigos grises de 2 dígitos

00 01 11 10

En este Código Gris, cada número difiere de su vecino en 1 dígito. 00->01->11->10->00 (tenga en cuenta que el código Gray es circular o se envuelve de abajo hacia arriba). Se puede crear un Código Gris de 3 dígitos reflejando (como un espejo) el Código Gris de 2 dígitos a través de un plano, y anteponiendo un 0 a los números en la parte superior de la tabla, y un 1 a los números en la parte inferior de la tabla.

Tabla\(\PageIndex{2}\): Códigos grises de 3 dígitos

000 001 011 \(\ \underline{010}\) 110 111 101 100

Una vez más que todos los valores de esta tabla difieren de los valores adyacentes en 1 dígito, pero además la tabla se ha agrupado en colecciones de agrupaciones de 2 bits. Por ejemplo, las filas 0 y 1 contienen ambas 00x, las filas 1 y 2 contienen 0x1, las filas 2 y 3 contienen 10x, las filas 3 y 4 contienen x10, etc (donde x es 0,1). Tenga en cuenta que una vez más la tabla se envuelve, por lo que las filas 7 y 0 contienen ambas x00.

Los códigos grises son útiles para particionar un espacio para agrupar elementos similares, y esta propiedad se utilizará en la siguiente sección de K-maps.

\(\PageIndex{2}\)Mapas de Karnaugh de 2 variables

Un mapa de Karnaugh (o simplemente K-map) es un mapeo de una tabla de verdad que divide la tabla de verdad para que los elementos que tienen los mismos valores se coloquen adyacentes entre sí. Entonces es más fácil ver qué términos son en común, y reducir la expresión booleana. Por ejemplo, un mapa K de 2 variables para una función F (A, B) se representaría de la siguiente manera, con los valores de A en filas y los valores de B en las columnas.

Tabla\(\PageIndex{3}\): Mapa K 2-Variable

A/B	0	1
0	A'B'	A'B
1	AB'	AB

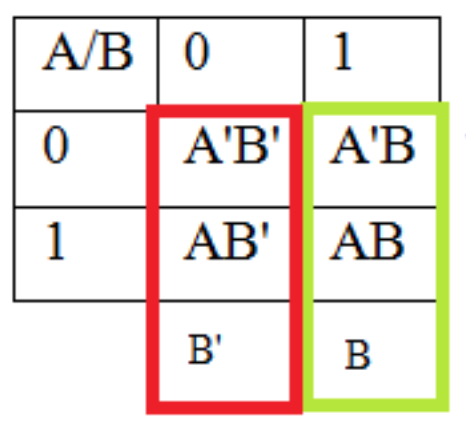
En esta tabla, las filas corresponden a A y No-A, y las columnas corresponden a B y No-B.

Tabla\(\PageIndex{4}\): A/A' para mapa K de 2 variables

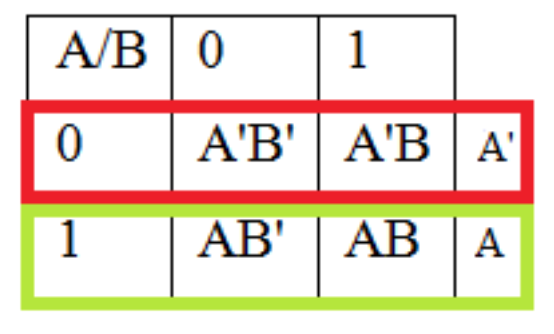
Tabla\(\PageIndex{5}\): B/B' para un mapa K de 2 variables

Dado que el mapa K ha agrupado los términos, es más fácil encontrar una ecuación booleana mínima. Por ejemplo, considere la siguiente tabla de verdad:

Tabla\(\PageIndex{6}\): Tabla de Verdad para problema de mapa K de 2 variables.

Entrada		Salida
A	B	Y
0	0	1
0	1	1
1	0	1
1	1	0

Esta tabla de la verdad se mapea con el siguiente mapa K. En este K-mapa se encuentran grupos de 2n ítems adyacentes, los cuales para un mapa K de 2 variables solo pueden ser grupos de 4, 2 y 1. En este mapa hay 2 grupos de 2, como se muestra a continuación.

Tabla\(\PageIndex{7}\): Resolviendo un mapa K de 2 variables

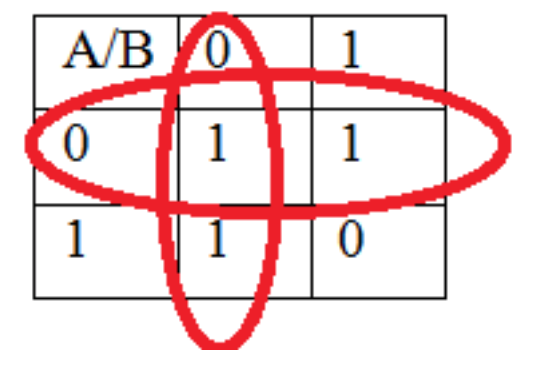
Los dos agrupamientos encontrados corresponden a A' y B', por lo que la ecuación final para este K-map es A'+B'.

Dos mapas K variables son triviales, y por lo tanto no muy interesantes. En las dos secciones siguientes se mostrará cómo resolver los mapas K para más variables 3 y 4.

\(\PageIndex{3}\)Mapas de Karnaugh de 3 variables

Los mapas K de 3 variables corresponden a funciones booleanas de la forma f (A, B, C). Los mapas K nuevamente permiten mapear una tabla de verdad para que las filas que difieren en 1 o 2 valores se coloquen una al lado de la otra. Para ello, se utilizan los Códigos Grises que se introdujeron anteriormente. Observe cómo los valores de las variables B y C se numeran como Códigos Gray en la tabla K-map de 3 variables.

Tabla\(\PageIndex{8}\): Mapa K de 3 variables

A/BC	00	01	11	10
0	A'B'C'	A'B'C	A'BC	A'BC'
1	AB'C'	AB'C	ABC	A'BC'

Obsérvese que una vez más este número ha dado como resultado regiones en el mapa K donde las variables difieren en 1 dígito, como se muestra a continuación. Tenga en cuenta que la región C' se envuelve alrededor de la mesa.

Tabla\(\PageIndex{9}\): Región A/A' de un mapa K de 3 variables

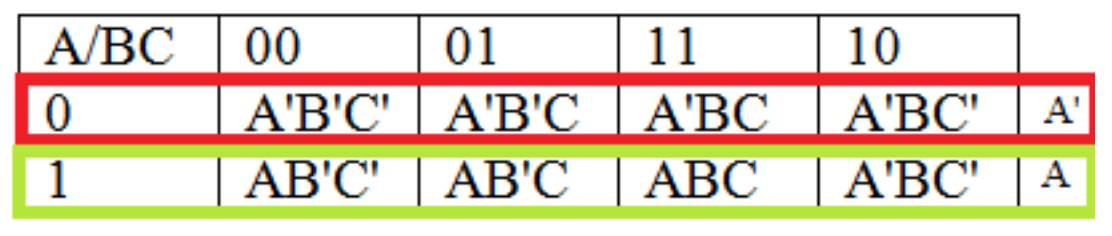
Tabla\(\PageIndex{10}\): Región B/B' de un mapa K de 3 variables

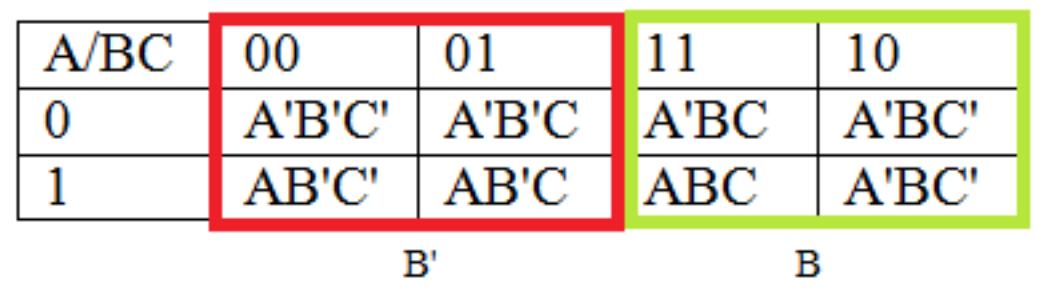
Tabla\(\PageIndex{11}\): Región C/C' de un mapa K de 3 variables

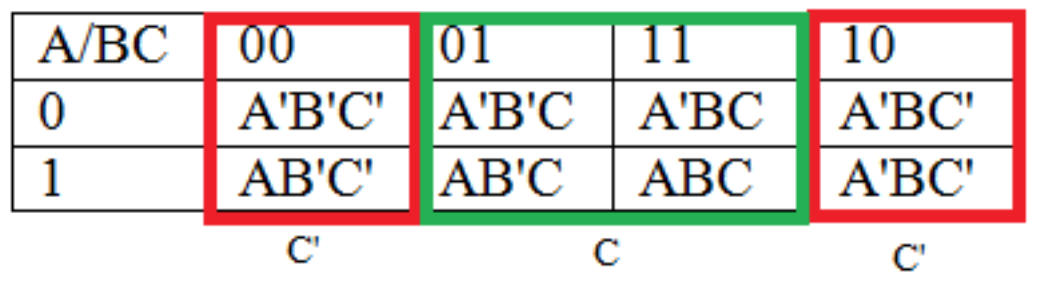
Para utilizar el mapa K para resolver 3 funciones variables, nuevamente se encuentran agrupaciones de 2n, que para un mapa K de 3 variables son 8, 4, 2 y 1. Cuanto mayor sea la agrupación, menores serán los términos, por lo que las agrupaciones de 8 se eligen sobre las agrupaciones de 4, las agrupaciones de 4 se eligen sobre las agrupaciones de 2 y las agrupaciones de 2 se eligen sobre las agrupaciones de 1.

El siguiente es un ejemplo de cómo usar un mapa K para resolver una expresión booleana. Considerar una función f (A, B, C) tiene la siguiente tabla de verdad:

Entrada			f (A, B, C)
A	B	C	Y
0	0	0	1
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

Esta expresión se puede representar como la siguiente suma de productos.

f (A, B, C) = σ (0, 4, 5, 6, 7)

La función mínima para este K-map consiste en un grupo de 4 y un grupo de 2, y corresponde a la ecuación f (A, B, C) = A+B'C'. Observe que la celda AB'C' se usa en ambas ecuaciones, que es la regla 5 de la tabla de relaciones booleanas, X+X = X, y significa que cualquier término en la suma se puede usar más de una vez para minimizar el circuito.

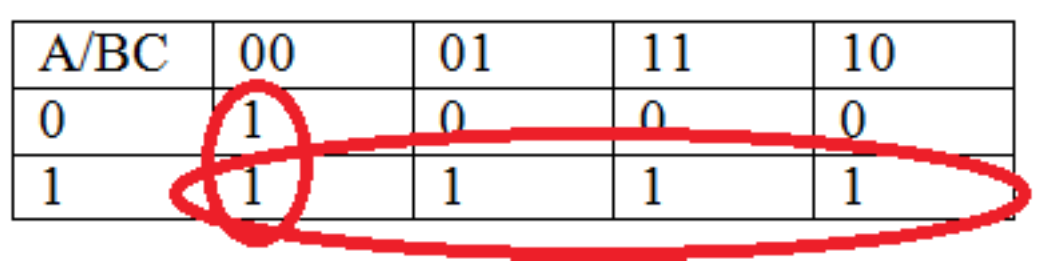
Para mostrar que la ecuación final corresponde a la tabla de verdad inicial, se utilizará álgebra para reducir la expresión de DNF a la forma final.

\ [\ begin {alineado}
\ mathrm {f (A, B, C)}
&= σ (0,\: 4,\: 5,\: 6,\: 7)\\
&=\ mathrm {A'B'C' + AB'C' + AB'C + ABC' + ABC}\\
&=\ mathrm {A'B'C' + AB'C' + AB'C' + AB'C + ABC' + ABC\ :( regla\: 5)}\\
&=\ mathrm {(A+A')\: B'C' + (AB' + AB) ( C+C')\: (regla\: 13)}\\
&=\ mathrm {(1)\: (B'C') + (AB' + AB)\: (1)\ :( regla\: 7)}\\
&=\ mathrm {B'C' + AB'+ AB\ :( regla\: 4)}\\
&=\ mathrm {(B'C') + A (B'+B)\ :( regla\: 13)}\\
&=\ mathrm {(B'C') + A (1)\ :( regla\: 7)}\\
&=\ mathrm {(B'C') + A\: (regla\: 4)}
\ end {alineado}\ nonumber\]

\(\PageIndex{4}\)Mapas de Karnaugh de 4 variables

Si bien existen mapas K mayores a 4 variables, requieren más de 2 dimensiones y por lo tanto son difíciles de resolver a mano, aunque existen formas algorítmicas de hacerlo y hay muchos programas en línea que pueden resolverlos. A este texto sólo le interesa presentar el concepto de mapas K y cómo se resuelven, por lo que terminará con la presentación de mapas K de 4 variables.

4-Los mapas K variables corresponden a funciones booleanas de la forma f (A, B, C, D). Los mapas K nuevamente permiten mapear una tabla de verdad para que las filas y columnas que difieren en 1 o 2 valores se coloquen una al lado de la otra. Para ello, se utilizan los Códigos Grises que se introdujeron anteriormente. Observe cómo los valores para las variables A, B y C, D se numeran como Códigos Gris en la tabla K-map de 3 variables.

AB/CD	00	01	11	10
00	A'B'C'D'	A'B'C'D	A'B'CD	A'B'CD'
01	A'BC'D'	A'B'D	A'BCD	A'BC'D'
11	ABC'D'	ABC'D	ABCD	ABCD'
10	AB'C'D'	AB'C'D	AB'CD	AB'CD'

Obsérvese que una vez más este número ha dado como resultado regiones en el mapa K donde las variables difieren en 1 dígito, como se muestra a continuación. Tenga en cuenta que las regiones B' y D' se envuelven alrededor de la mesa.

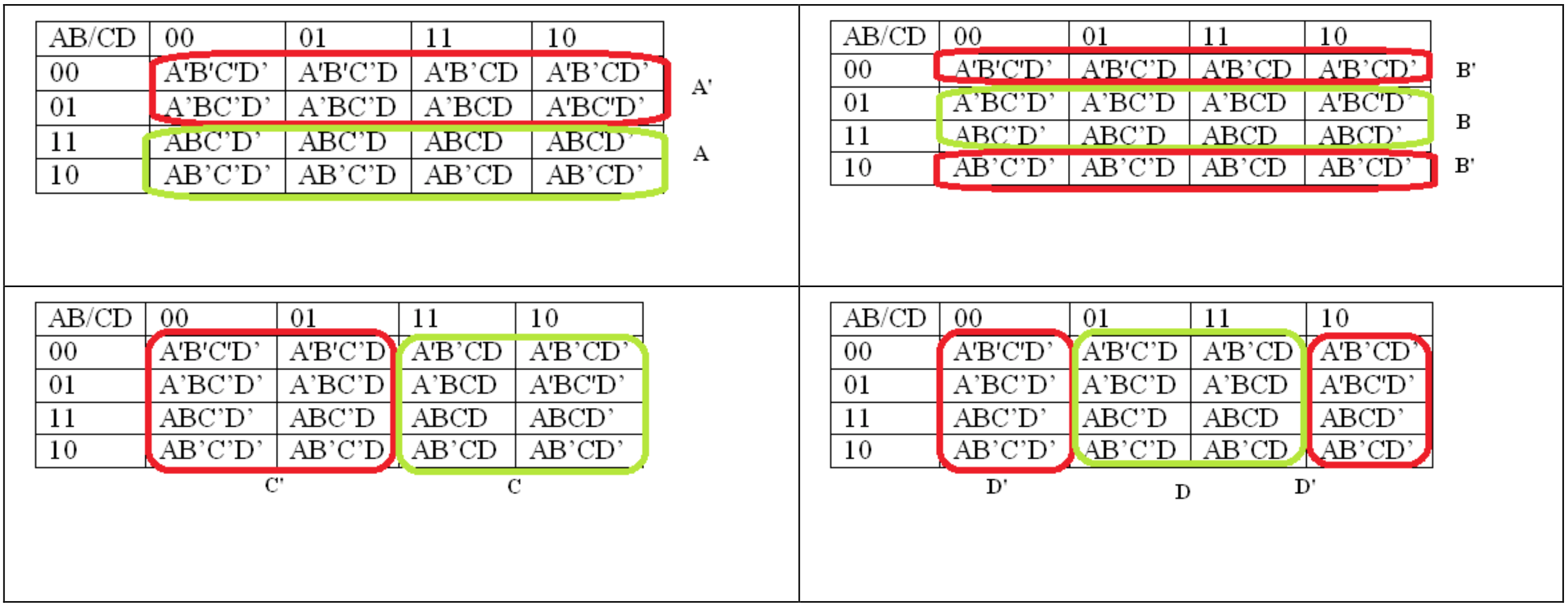
Para utilizar el mapa K para resolver 3 funciones variables, nuevamente se encuentran agrupaciones de 2 ⁿ, que para un mapa K de 4 Variables son 16., 8, 4, 2 y 1. Cuanto mayor sea la agrupación, menores serán los términos, por lo que las agrupaciones de 16 se eligen sobre las agrupaciones de 8, las agrupaciones de 8 se eligen sobre las agrupaciones de 4, las agrupaciones de 4 se eligen sobre las agrupaciones de 2, y las agrupaciones de 2 se eligen sobre las agrupaciones de 1.

El siguiente es un ejemplo de cómo usar un mapa K para resolver una expresión booleana. Considerar una función f (A, B, C) tiene la siguiente tabla de verdad:

Entrada				f (A, B, C)
A	B	C	D	Y
0	0	0	0	1
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	1
0	1	0	1	1
0	1	1	0	1
0	1	1	1	1
1	0	0	0	1
1	0	0	1	0
1	0	1	0	0
1	0	1	1	0
1	1	0	0	1
1	1	0	1	1
1	1	1	0	1
1	1	1	1	1

Esta expresión se puede representar como la siguiente suma de productos.

f (A, B, C) = σ (0, 4, 5, 6, 7, 8, 12, 13, 14, 15)

La función mínima para este K-map consiste en un grupo de 8 y un grupo de 4, y corresponde a la ecuación f (A, B, C) = B + C'D'. Tenga en cuenta que las celdas A'BC'D' y ABC'D' se utilizan en ambas ecuaciones, que es la regla 5 de la tabla de relaciones booleanas, X+X = X, y significa que cualquier término en la suma se puede usar más de una vez para minimizar el circuito.

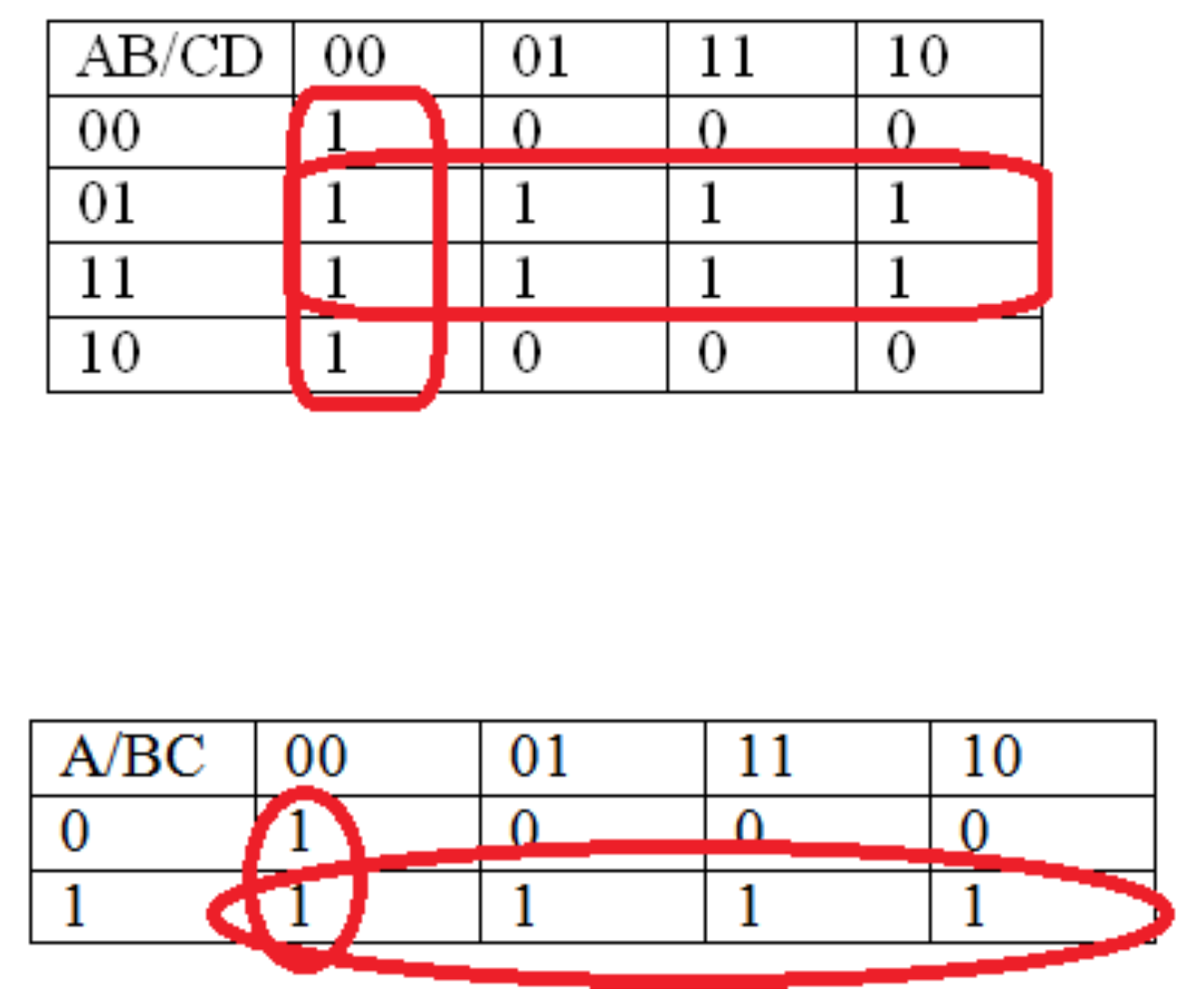
Para mostrar que la ecuación final corresponde a la tabla de verdad inicial, se puede utilizar álgebra booleana. La derivación de la ecuación final del DNF se deja como un ejercicio.

\(\PageIndex{5}\)No me importan las condiciones

En ocasiones al especificar una ecuación hay una serie de situaciones en las que no se usa la entrada. Si no se usa la entrada, entonces se puede usar cualquier valor (0 o 1), y estos se llaman condiciones no importan. Por ejemplo, considere una pantalla de 7 segmentos que se utiliza para muchos relojes de tiempo para eventos deportivos. La pantalla consta de 7 segmentos que se utilizan para mostrar los 10 números decimales 0.. 9. A continuación se muestra una visualización de 7 segmentos junto con los nombres de cada segmento (A.. G).

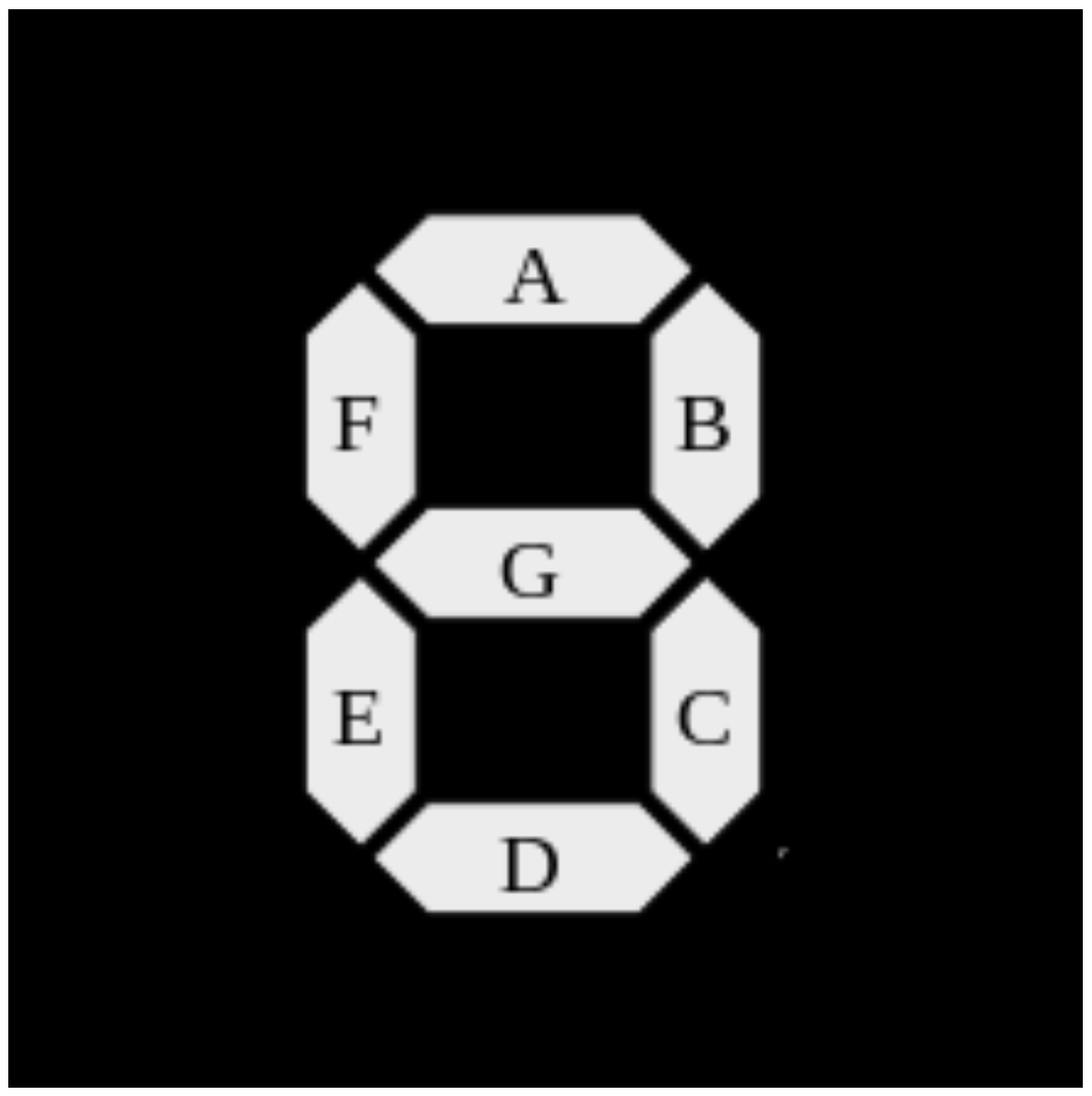
Cada dígito 0-9 encenderá 1 o más segmentos para crear el número. Por ejemplo, el dígito 0 iluminaría los segmentos A, B, C, D, E, F; el número 1 iluminaría los segmentos B, C; el número 2 iluminaría los segmentos A, B, D, E, G; etc. Por lo tanto, habrá 7 funciones booleanas, una para cada segmento.

A continuación, sabiendo que se pueden representar 10 dígitos usando un mínimo de 4 bits, se puede crear una tabla de verdad donde los 4 dígitos de entrada representan el número decimal, y se desarrolla una tabla de verdad para cada uno de los 7 segmentos que componen el número. Al hacer esto, tenga en cuenta que los valores de entrada para la tabla de verdad siempre deben estar entre 0-9, por lo que hay 6 valores (10-15) que no se utilizan, por lo que nunca se accede a esas filas de la tabla. Los valores para los segmentos para esas filas son no importa porque nunca se usan; el componente no usa esos valores, por lo que no le importa cómo se establecen. Esto da el resultado para la tabla de verdad de visualización de 7 segmentos, donde x=No me importa, que se muestra a continuación.

Entrada					Salida
A	B	C	D		A	B	C	D	E	F	G
0	0	0	0		1	1	1	1	1	1	0
0	0	0	1		0	1	1	0	0	0	0
0	0	1	0		1	1	0	1	1	0	1
0	0	1	1		1	1	1	1	0	0	1
0	1	0	0		0	1	1	0	0	1	1
0	1	0	1		1	0	1	1	0	1	1
0	1	1	0		1	0	1	1	1	1	1
0	1	1	1		1	1	1	0	0	0	0
1	0	0	0		1	1	1	1	1	1	1
1	0	0	1		1	1	1	0	0	1	1
1	0	1	0		X	X	X	X	X	X	X
1	0	1	1		X	X	X	X	X	X	X
1	1	0	0		X	X	X	X	X	X	X
1	1	0	1		X	X	X	X	X	X	X
1	1	1	0		X	X	X	X	X	X	X
1	1	1	1		X	X	X	X	X	X	X

El mapa K para cada segmento ahora se puede evaluar para dar la expresión booleana mínima correspondiente. Los don't cares (Xs) en el mapa son importantes porque podemos asumir que son 1 cuando nos ayudan a minimizar una expresión, y asumir que son 0 de lo contrario. En definitiva, podemos utilizarlos para crear agrupaciones más grandes, pero no tienen que ser utilizadas.

El mapa K para el segmento A es el siguiente:

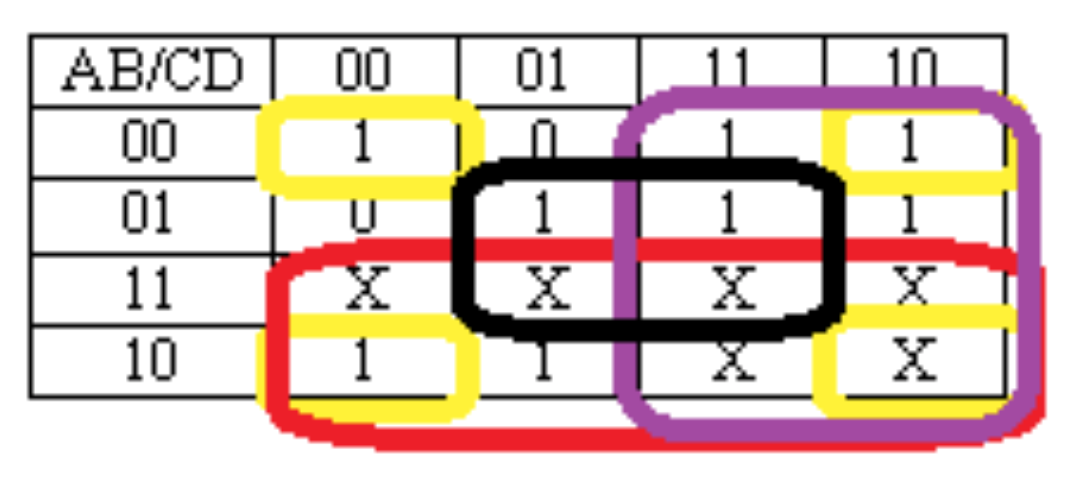
El resultado son dos grupos de 8 (en rojo y morado) correspondientes a A y B, y dos grupos de 4, uno (en negro) correspondiente a BD, y uno (en amarillo, cruzando las 4 esquinas del mapa) correspondiente a B'C', dando como resultado la siguiente ecuación para el segmento A,

fA (A, B, C, D) = A + C + BD + B'D'