2.6:\(T\) or Chain Scattering Parameters of Cascaded Two-Port Networks

Los\(T\) parámetros, también conocidos como parámetros de dispersión de cadena, son una forma de parámetros de dispersión en cascada. Son similares a\(S\) los parámetros regulares y se pueden expresar en términos de las ondas de potencia\(a\) y\(b\) raíz u ondas de voltaje viajeras. Dos redes de dos puertos, A y B, en cascada se muestran en la Figura\(\PageIndex{1}\). Aquí\((A)\) y\((B)\) se utilizan como superíndices para distinguir los parámetros de cada red de dos puertos, pero los subíndices\(A\) y\(B\) se utilizan para cantidades matriciales. Desde

\[\label{eq:1}a_{2}^{(A)}=b_{1}^{(B)}\quad\text{and}\quad b_{2}^{(A)}=a_{1}^{(B)} \]

Figura\(\PageIndex{1}\): Dos puertos en cascada.

es conveniente poner los\(b\) parámetros\(a\) y en forma de cascada, lo que lleva a la siguiente matriz de cadena de dos puertos o representación\(T\) matricial (con respecto a la Figura 2.4.3):

\[\label{eq:2} \left[\begin{array}{c}{a_{1}}\\{b_{1}}\end{array}\right] =\left[\begin{array}{cc}{T_{11}}&{T_{12}}\\{T_{21}}&{T_{22}}\end{array}\right]\left[\begin{array}{c}{b_{2}}\\{a_{2}}\end{array}\right] \]

donde la\(\text{T}\) matriz o matriz de dispersión de cadena es

\[\label{eq:3}\mathbf{T}=\left[\begin{array}{cc}{T_{11}}&{T_{12}}\\{T_{21}}&{T_{22}}\end{array}\right] \]

\(\mathbf{T}\)es muy similar a la matriz de transferencia de dispersión\((\:^{S}\mathbf{T})\) de la Sección 2.3.7. La única diferencia es el orden de los\(b\) componentes\(a\) y. Te encontrarás con ambas formas, así que ten cuidado de que entiendas cuál se está utilizando. Ambas formas se utilizan para la misma función: redes de dos puertos en cascada. Las relaciones entre\(\mathbf{T}\) y\(\mathbf{S}\) están dadas por

\[\label{eq:4}\mathbf{T}=\left[\begin{array}{cc}{S_{21}^{-1}}&{-S_{21}^{-1}S_{22}}\\{S_{21}^{-1}S_{11}}&{S_{12}-S_{11}S_{21}^{-1}S_{22}}\end{array}\right] \]

\[\label{eq:5}\mathbf{S}=\left[\begin{array}{cc}{T_{21}T_{11}^{-1}}&{T_{22}-T_{21}T_{11}^{-1}T_{12}}\\{T_{11}^{-1}}&{-T_{11}^{-1}T_{12}}\end{array}\right] \]

Para una red de dos puertos, usando ecuaciones\(\eqref{eq:1}\) y\(\eqref{eq:2}\),

\[\label{eq:6}\left[\begin{array}{c}{a_{1}^{(A)}}\\{b_{1}^{(A)}}\end{array}\right]=\mathbf{T}_{A}\left[\begin{array}{c}{b_{2}^{(A)}}\\{a_{2}^{(A)}}\end{array}\right]\quad\text{and}\quad\left[\begin{array}{c}{a_{1}^{(B)}}\\{b_{1}^{(B)}}\end{array}\right]=\mathbf{T}_{B}\left[\begin{array}{c}{b_{2}^{(B)}}\\{a_{2}^{(B)}}\end{array}\right] \]

por lo tanto

\[\label{eq:7}\left[\begin{array}{c}{a_{1}^{(A)}}\\{b_{1}^{(A)}}\end{array}\right]=\mathbf{T}_{A}\mathbf{T}_{B}\left[\begin{array}{c}{b_{2}^{(B)}}\\{a_{2}^{(B)}}\end{array}\right] \]

Para redes de dos puertos en\(n\) cascada, Ecuación\(\eqref{eq:7}\) generaliza a

\[\label{eq:8}\left[\begin{array}{c}{a_{1}^{(1)}}\\{b_{1}^{(1)}}\end{array}\right]=\mathbf{T}_{1}\mathbf{T}_{2}\ldots\mathbf{T}_{n}\left[\begin{array}{c}{b_{2}^{(n)}}\\{a_{2}^{(n)}}\end{array}\right] \]

y así la\(\mathbf{T}\) matriz de la red en cascada es el producto matricial de las\(\mathbf{T}\) matrices de los dos puertos individuales.

Anteriormente, en la Sección 2.3.7, se introdujeron los parámetros de transferencia de dispersión. Tanto los parámetros de dispersión de cadena como los parámetros de transferencia de dispersión se denominan\(T\) parámetros. Tenga cuidado de denotar qué forma se está utilizando.

Ejemplo\(\PageIndex{1}\): Development of Chain Scattering Parameters

Derive los\(T\) parámetros de la red de dos puertos hacia la derecha usando una impedancia de referencia\(Z_{0}\).

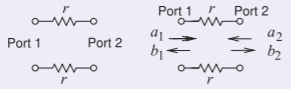
Figura\(\PageIndex{2}\)

Solución

\(\underline{\text{Derivation of }T_{11}}\)

Terminar\(\mathsf{2}\) el puerto en una carga coincidente para que\(a_{2} = 0\). Entonces la ecuación\(\eqref{eq:2}\) se convierte\(a_{1} = T_{11}b_{2}\) y\(b_{1} = T_{21}b_{2}\) así

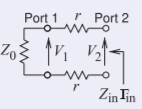
Figura\(\PageIndex{3}\)

\[\label{eq:9}\Gamma_{\text{in}}=b_{1}/a_{1}=T_{21}/T_{11} \]

Ahora\(Z_{\text{in}}=2r+Z_{0}\), por lo tanto

\[\begin{aligned}\Gamma_{\text{in}}&=\frac{Z_{\text{in}}-Z_{0}}{Z_{\text{in}}+Z_{0}} \\ &=\frac{2r+Z_{0}-Z_{0}}{2r+Z_{0}+Z_{0}}=\frac{r}{r+Z_{0}}\end{aligned}\nonumber \]

Así

\[\label{eq:10}\Gamma_{\text{in}}=\frac{T_{21}}{T_{11}}=\frac{r}{r+Z_{0}} \]

La siguiente etapa se\(b_{2}\) relaciona con\(a_{1}\) y ya que ambos puertos tienen la misma impedancia de referencia\(a\) y\(b\) pueden ser reemplazados por voltajes de desplazamiento

\[\begin{aligned}V_{1}=(V_{1}^{+}+V_{1}^{-})&=V_{1}^{+}(1+\Gamma_{\text{in}}) \\ &=V_{1}^{+}\frac{2r+Z_{0}}{r+Z_{0}}\end{aligned}\nonumber \]

Uso de división de voltaje (y desde\(V_{2}^{+} = a_{2} = 0\))

\[\begin{align}V_{2}=V_{2}^{-}&=\frac{Z_{0}}{2r+Z_{0}}V_{1}\nonumber \\ &=V_{1}^{+}\frac{Z_{0}}{2r+Z_{0}}\frac{2r+Z_{0}}{r+Z_{0}}\nonumber \\ V_{2}^{-}&=V_{1}^{+}\frac{Z_{0}}{r+Z_{0}}\nonumber \\ \label{eq:11}T_{11}&=\frac{V_{1}^{+}}{V_{2}^{-}}=\frac{a_{1}}{b_{2}}=\frac{r+Z_{0}}{Z_{0}}\end{align} \]

\(\underline{\text{Derivation of }T_{21}}\)

Combinando ecuaciones\(\eqref{eq:10}\) y\(\eqref{eq:11}\)

\[\label{eq:12}T_{21}=\Gamma_{\text{in}}T_{11}=\frac{r}{r+Z_{0}}\frac{r+Z_{0}}{Z_{0}}=\frac{r}{Z_{0}} \]

\(\underline{\text{Derivation of }T_{22}}\)

Terminar\(\mathsf{2}\) el puerto en una carga coincidente para que\(a_{1} = 0\). Entonces la Ecuación\(\eqref{eq:2}\) se convierte

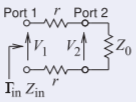
Figura\(\PageIndex{4}\)

\[\begin{align}0&=T_{11}b_{2}+T_{12}a_{2}\nonumber \\ \label{eq:13}\Gamma_{\text{in}}&=\frac{b_{2}}{a_{2}}=\frac{-T_{12}}{T_{11}}\to T_{12}=-T_{11}\Gamma_{\text{in}} \\ b_{1}&=T_{21}b_{2}+T_{22}a_{2} \\ \label{eq:14}\frac{b_{1}}{a_{2}}&=T_{21}\frac{b_{2}}{a_{2}}+T_{22}\end{align} \]

Ahora\(Z_{\text{in}} = 2r + Z_{0}\) y así

\[\label{eq:15}\Gamma_{\text{in}}=\frac{2r+Z_{0}-Z_{0}}{2r+Z_{0}+Z_{0}}=\frac{r}{r+Z_{0}} \]

Uso de división de voltaje

\[\begin{align}V_{1}&=V_{1}^{-}=\frac{Z_{0}}{2r+Z_{0}}V_{2}=\frac{Z_{0}}{2r+Z_{0}}V_{2}^{+}(1+\Gamma_{\text{in}})\nonumber \\ &=V_{2}^{+}\frac{Z_{0}}{2r+Z_{0}}\frac{2r+Z_{0}}{r+Z_{0}}=V_{2}^{+}\frac{Z_{0}}{r+Z_{0}}\nonumber \\ \label{eq:16}\frac{V_{1}^{-}}{V_{2}^{+}}&=\frac{b_{1}}{a_{2}}=\frac{Z_{0}}{r+Z_{0}}\end{align} \]

Sustitución de ecuaciones\(\eqref{eq:15}\) y\(\eqref{eq:16}\) en Ecuación\(\eqref{eq:14}\) y reorganización

\[T_{22}=\frac{Z_{0}}{r+Z_{0}}-T_{21}\frac{r}{r+Z_{0}}\nonumber \]

Combinando esto con Ecuación\(\eqref{eq:12}\)

\[\label{eq:17}T_{22}=\frac{Z_{0}}{r+Z_{0}}-\frac{r}{Z_{0}}\frac{r}{r+Z_{0}}=\frac{Z_{0}^{2}-r^{2}}{Z_{0}(r+Z_{0})} \]

\(\underline{\text{Derivation of }T_{12}}\)

Combinando ecuaciones\(\eqref{eq:11}\),\(\eqref{eq:13}\) y\(\eqref{eq:15}\)

\[\label{eq:18}T_{12}=-\frac{r+Z_{0}}{Z_{0}}\frac{r}{r+Z_{0}}=-\frac{r}{Z_{0}} \]

\(\underline{\text{Summary}}\):

Los\((T)\) parámetros de la matriz de dispersión de cadena se dan en Ecuaciones\(\eqref{eq:11}\)\(\eqref{eq:12}\),\(\eqref{eq:17}\),, y\(\eqref{eq:18}\).

Ejemplo\(\PageIndex{2}\): Cascading Chain Scattering Parameters

Desarrollar los parámetros de dispersión de la cadena de la red a la derecha. Utilice una impedancia de referencia\(Z_{\text{REF}} = Z_{0}\), la impedancia característica de las líneas.

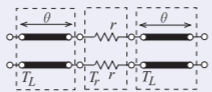
Figura\(\PageIndex{5}\)

Solución

La red comprende una línea de transmisión de longitud eléctrica\(\theta\) en cascada con una red resistiva y otra línea de la misma longitud eléctrica. A partir de la Ecuación (2.5.3) los parámetros de dispersión de la línea de transmisión son

\[\label{eq:19}\mathbf{S}_{L}=\left[\begin{array}{cc}{0}&{\text{e}^{-\jmath\theta}}\\{\text{e}^{-\jmath\theta}}&{0}\end{array}\right] \]

De\(\eqref{eq:4}\) la ecuación la matriz de dispersión de cadena de la línea es

\[\label{eq:20}\mathbf{T}_{L}=\left[\begin{array}{cc}{\text{e}^{\jmath\theta}}&{0}\\{0}&{\text{e}^{-\jmath\theta}}\end{array}\right] \]

De Ejemplo\(\PageIndex{1}\) la matriz de dispersión de cadena de la red resistiva es

\[\label{eq:21}\mathbf{T}_{r}=\frac{1}{Z_{0}}\left[\begin{array}{cc}{gr+Z_{0}}&{-r}\\{r}&{(Z_{0}^{2}-r^{2})/(r+Z_{0})}\end{array}\right] \]

Dando la matriz de dispersión de cadena de la cascada;

\[\label{eq:22}\begin{array}{l}{T_{LrL}=T_{L}T_{r}T_{L}} \\ {\frac{1}{Z_{0}}\left[\begin{array}{cc}{(r+Z_{0})\text{e}^{2\jmath\theta}}&{-r}\\{r}&{(Z_{0}^{2}-r^{2})/(r+Z_{0})\text{e}^{-2\jmath\theta}}\end{array}\right]}\end{array} \]

Ejemplo\(\PageIndex{3}\): Input Reflection Coefficient of a Terminated Two-Port

Cuál es el coeficiente de reflexión de entrada en términos de parámetros de dispersión de cadena de los dos puertos terminados a la derecha donde los dos puertos se describen por sus parámetros de dispersión de cadena.

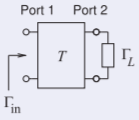
Figura\(\PageIndex{6}\)

Solución

Las relaciones de parámetros de dispersión de cadena son

\[\left[\begin{array}{c}{a_{1}}\\{b_{1}}\end{array}\right]=\left[\begin{array}{cc}{T_{11}}&{T_{12}}\\{T_{21}}&{T_{22}}\end{array}\right]\left[\begin{array}{c}{b_{2}}\\{a_{22}}\end{array}\right]\nonumber \]

Ampliar esta ecuación matricial y usar la sustitución\(a_{2} = \Gamma_{L}b_{2}\)

\[\begin{align}\label{eq:23}a_{1}&=T_{11}b_{2}+T_{12}\Gamma_{L}b_{2} \\ \label{eq:24}b_{1}&+T_{21}b_{2}+T_{22}\Gamma_{L}b_{2}\end{align} \]

Multiplicar Ecuación\(\eqref{eq:23}\) por\((T_{21} + T_{22}\Gamma_{L})\) y Ecuación\(\eqref{eq:24}\) por\((T_{11} +T_{12}\Gamma_{L})\) y luego restar

\[\begin{aligned}(T_{21} + T_{22}\Gamma_{L})a_{1} &= (T_{21} + T_{22}\Gamma_{L})(T_{11}b_{2} + T_{12}\Gamma_{L})b_{2}\nonumber \\ (T_{11} + T_{12}\Gamma_{L})b_{1} &= (T_{11} + T_{12}\Gamma_{L})(T_{21}b_{2} + T_{22}\Gamma_{L})b_{2}\nonumber \\ (T_{21} + T_{22}\Gamma_{L})a_{1} &= (T_{11} + T_{12}\Gamma_{L})b_{1}\nonumber\end{aligned} \nonumber \]

Así, el coeficiente de reflexión de entrada es

\[\label{eq:25}\Gamma_{\text{in}}=\frac{b_{1}}{a_{1}}=\frac{T_{21}+T_{22}\gamma_{L}}{T_{11}+T_{12}\gamma_{L}} \]

Consideremos ahora una línea de transmisión de longitud eléctrica\(\theta\) e impedancia característica\(Z_{0}\) (ver la figura b) en cascada con los dos puertos.

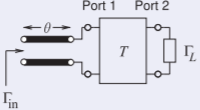
Figura\(\PageIndex{7}\)

El coeficiente de reflexión de entrada ahora se encuentra determinando primero la matriz de dispersión de cadena total de la cascada:

\[\begin{aligned}^{\mathbf{T}}\mathbf{T}&=\mathbf{T}_{\mathbf{L}}\mathbf{T}=\left[\begin{array}{cc}{\text{e}^{\jmath\theta}}&{0}\\{0}&{\text{e}^{-\jmath\theta}}\end{array}\right]\left[\begin{array}{cc}{T_{11}}&{T_{12}}\\{T_{21}}&{T_{22}}\end{array}\right]\nonumber \\ &=\left[\begin{array}{cc}{T_{11}\text{e}^{\jmath\theta}}&{T_{12}\text{e}^{\jmath\theta}}\\{T_{21}\text{e}^{-\jmath\theta}}&{T_{22}\text{e}^{-\jmath\theta}}\end{array}\right]\left[\begin{array}{cc}{^{T}T_{11}}&{^{T}T_{12}}\\{^{T}T_{21}}&{^{T}T_{22}}\end{array}\right]\nonumber\end{aligned} \nonumber \]

Así, el coeficiente de reflexión de entrada es ahora

\[\begin{align}\Gamma_{\text{in}}&=\frac{b_{1}}{a_{1}}=\frac{^{T}T_{21}+\:^{T}T_{22}\Gamma_{L}}{^{T}T_{11}+\:^{T}T_{12}\Gamma_{L}}\nonumber \\ &=\frac{T_{21}\text{e}^{-\jmath\theta}+T_{22}\text{e}^{-\jmath\theta}\Gamma_{L}}{T_{11}\text{e}^{\jmath\theta}+T_{12}\text{e}^{\jmath\theta}\Gamma_{L}}\nonumber \\ \label{eq:26}&=\text{e}^{-2\jmath\theta}\left(\frac{T_{21}+T_{22}\Gamma_{L}}{T_{11}+T_{12}\Gamma_{L}}\right)\end{align} \]

Si la carga es ahora un cortocircuito\(\Gamma_{L} = −1\) y el coeficiente de reflexión de entrada de la línea y la cascada de dos puertos es

\[\label{eq:27}\Gamma_{\text{in}}=\text{e}^{-2\jmath\theta}\left(\frac{T_{21}-T_{22}}{T_{11}-T_{12}}\right) \]

2.6.1 Red de dos puertos terminada

Un puerto de dos puertos con Puerto 2 terminado en una carga con coeficiente de reflexión\(\Gamma_{L}\) se muestra en la Figura 2.7.1 y\(a_{2} =\Gamma_{L}b_{2}\). Sustituir esto en la Ecuación\(\eqref{eq:2}\) lleva a

\[a_{1} = (T_{11} + T_{12}\Gamma_{L})b_{2}\quad\text{and}\quad b_{1} = (T_{21} + T_{22}\Gamma_{L})b_{2}\nonumber \]

eliminando\(b_{2}\) resultados en

\[\label{eq:28}\Gamma_{\text{in}}=\frac{b_{1}}{a_{1}}=\frac{T_{21}+T_{22}\Gamma_{L}}{T_{11}+T_{12}\Gamma_{L}} \]