5.2:\(Q\) Factor
- Page ID
- 80802
Los inductores y capacitores de RF también tienen pérdida y elementos parásitos. Con los inductores hay resistencia en serie y capacitancia de derivación principalmente de capacitancia entre devanados, mientras que con los capacitores habrá resistencia de derivación e inductancia en serie. Un inductor o condensador práctico es limitado
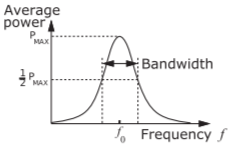
Figura\(\PageIndex{1}\): Característica de transferencia de un circuito resonante. (La función de transferencia es\(V/I\) para el circuito resonante paralelo de la Figura\(\PageIndex{2}\) (a) y\(I/V\) para el circuito resonante en serie de la Figura\(\PageIndex{2}\) (b).)
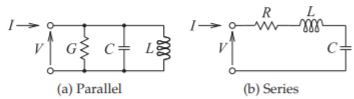
Figura\(\PageIndex{2}\): Circuitos resonantes de segundo orden.
a operar por debajo de la frecuencia autorresonante determinada por la inductancia y capacitancia misma que resuena con sus parásitos reactivos. El impacto de la pérdida se cuantifica por el\(Q\) factor (el factor de calidad). \(Q\)está vagamente relacionado con el ancho de banda en general y la relación estricta se basa en la respuesta de una conexión en serie o en paralelo de una resistencia (\(R\)), un inductor (\(L\)) y un condensador (\(C\)). La respuesta de una\(RLC\) red se describe mediante una ecuación diferencial de segundo orden con la conclusión de que el ancho de banda\(3\text{ dB}\) fraccional de la respuesta (es decir, cuando la respuesta de potencia está en su nivel de media potencia por debajo de su respuesta pico) es\(1/Q\). (El ancho de banda fraccional es\(\Delta f /f_{0}\) donde\(f_{0} = f_{r}\) está la frecuencia resonante en el centro de la banda y\(\Delta f\) es el\(3\text{ dB}\) ancho de banda). Esto no es cierto para ninguna red que no sea un circuito de segundo orden, pero como principio rector, las redes con\(Q\) s superiores tendrán anchos de banda más estrechos.
5.2.1 Definición
El\(Q\) factor de un componente en frecuencia\(f\) se define como la relación de\(2\pi f\) veces la energía máxima almacenada a la energía perdida por ciclo. En un circuito resonante de elementos grumados, la energía almacenada se transfiere entre un inductor, que almacena energía magnética, y un condensador, que almacena energía eléctrica, y de nuevo cada período. Los resonadores distribuidos funcionan de la misma manera, intercambiando energía almacenada en formas eléctricas y magnéticas, pero con la energía almacenada espacialmente. El factor de calidad es
\[\label{eq:1}Q=2\pi f_{r}\left(\frac{\text{average energy stored in the resonator at }f_{r}}{\text{power lost in the resonator}}\right) \]
donde\(f_{1} = \omega_{r}/(2π)\) está la frecuencia resonante.
Una respuesta simple se muestra en la Figura\(\PageIndex{1}\). Para un circuito resonante paralelo con elementos\(L,\: C,\) y\(G = 1/R\) (ver Figura\(\PageIndex{2}\) (a)),
\[\label{eq:2}Q=\omega_{r}C/G=1/(\omega_{r}LG) \]
donde\(f_{r} = \omega_{r}/(2π)\) es la frecuencia resonante y es la frecuencia a la que se almacena la cantidad máxima de energía en un resonador. La conductancia,\(G\), describe la energía perdida en un ciclo. Para un circuito resonante en serie (Figura\(\PageIndex{2}\) (b)) con\(L,\: C,\) y\(R\) elementos,
\[\label{eq:3}Q=\omega_{r}L/R=1/(\omega_{r}CR) \]
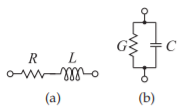
Figura\(\PageIndex{3}\): Elementos de pérdida de inductores y capacitores prácticos: (a) un inductor tiene una resistencia en serie\(R\); y (b) para un condensador, el mecanismo de pérdida dominante es una conductancia de derivación\(G = 1/R\).
Estos circuitos resonantes de segundo orden tienen una característica de transferencia de paso de banda (ver Figura\(\PageIndex{1}\))\(Q\) siendo la inversa del ancho de banda fraccional del resonador. El ancho de banda fraccional,\(\Delta f /f_{r}\), se mide en los puntos de media potencia como se muestra en la Figura\(\PageIndex{1}\). (también\(\Delta f\) se conoce como el ancho de\(−3\text{ dB}\) banda de dos lados.) Entonces
\[\label{eq:4}Q=f_{r}/\Delta f \]
Por lo tanto,\(Q\) es una medida de la nitidez de la respuesta de frecuencia de paso de banda. La determinación del\(Q\) uso de la medición del ancho de banda junto con la Ecuación a menudo no\(\eqref{eq:4}\) es muy precisa, por lo que se prefiere otra definición que utilice el cambio de fase mucho más sensible en resonancia cuando se están utilizando mediciones. \(\phi\)Al ser la fase (en radianes) de la característica de transferencia, la definición de\(Q\) es ahora
\[\label{eq:5}Q=\frac{\omega_{r}}{2}\left|\frac{d\phi}{d\omega}\right| \]
\(\eqref{eq:5}\)La ecuación es otra definición equivalente de\(Q\) para circuitos\(RLC\) resonantes paralelos\(RLC\) o en serie. Es significativo hablar\(Q\) del de circuitos distintos de los circuitos de tres elementos\(RLC\), y entonces su significado es siempre una relación de la energía almacenada a la energía disipada por ciclo. La\(Q\) de estas estructuras ya no puede ser determinada por el ancho de banda o por la velocidad de cambio de fase.
5.2.2\(Q\) de Elementos Agrumeados
\(Q\)también se utiliza para caracterizar la pérdida de inductores y capacitores agrupados. Los inductores tienen una resistencia en serie\(R\), y el mecanismo de pérdida principal de un condensador es una conductancia de derivación\(G\) (ver Figura\(\PageIndex{3}\)).
El\(Q\) de un inductor a frecuencia\(f =\omega /(2\pi )\) con una resistencia\(R\) e inductancia en serie\(L\) es
\[\label{eq:6}Q_{\text{INDUCTOR}}=\frac{\omega L}{R} \]
Dado que\(R\) es aproximadamente constante con respecto a la frecuencia para un inductor, el\(Q\) variará con la frecuencia.
El\(Q\) de un condensador con una conductancia de derivación\(G\) y capacitancia\(C\) es
\[\label{eq:7}Q_{\text{CAPACITOR}}=\frac{\omega C}{G} \]
\(G\)se debe principalmente a los mecanismos de pérdida de relajación del dieléctrico de un condensador y por lo tanto varía linealmente con la frecuencia. Así el\(Q\) de un condensador es casi constante con respecto a la frecuencia. Para componentes de microondas invariablemente\(Q_{\text{CAPACITOR}} ≫ Q_{\text{INDUCTOR}}\), y\(Q_{\text{INDUCTOR}}\) es más pequeño que el\(Q\) de las redes de línea de transmisión. Por lo tanto, si la longitud de una línea de transmisión no es demasiado larga, se prefieren las redes de líneas de transmisión. Si se deben utilizar elementos agrupados, se debe minimizar el uso de inductores.
5.2.3\(Q\) Factor cargado
El\(Q\) de un componente como se define en la sección anterior se llama el descargado\(Q,\: Q_{U}\). Sin embargo, si un componente se va a medir o utilizar de alguna manera, es necesario acoplar energía dentro y fuera de él. El\(Q\) se reduce y así el ancho de banda del resonador se incrementa por la potencia perdida al circuito externo para que el cargado\(Q\), luego el cargado\(Q\) se
\[\begin{align}Q_{L}&=2\pi f_{0}\left(\frac{\text{average energy stored in the resonator at }f_{0}}{\text{power lost in the resonator and to the external circuit}}\right)\nonumber \\ \label{eq:8}&=\frac{1}{1/Q+1/Q_{X}}\end{align} \]
donde\(Q_{X}\) se llama el externo\(Q\). \(Q_{L}\)representa la potencia extraída del circuito resonante.
Entonces un\(LCG\) circuito paralelo con elementos\(L_{r},\: C_{r},\) y\(G_{r}\) (en resonancia) cargado por una conductancia de derivación\(G_{l}\) tiene
\[\label{eq:9}Q_{U}=\omega_{r}C_{r}/G_{r}=1/(\omega_{r}L_{r}G_{r}) \]
y
\[\label{eq:10}Q_{L}=\omega_{r}C_{r}/(G_{r}+G_{l}) \]
Así
\[\label{eq:11}\frac{1}{Q_{L}}=\frac{1}{Q_{U}}+\frac{1}{Q_{X}} \]
o
\[\label{eq:12}Q_{X}=\left(\frac{1}{Q_{L}}-\frac{1}{Q_{U}}\right)^{-1} \]
\(Q_{X}\)se llama externo\(Q\), y describe el efecto de la carga. \(Q_{L}\)es el\(Q\) que en realidad se mediría. \(Q_{U}\)normalmente necesita ser determinado, pero si la carga se mantiene muy pequeña,\(Q_{L}\approx Q_{U}\).
5.2.4 Resumen de los Inmuebles de\(Q\)
En resumen:
- \(Q\)se define adecuadamente y se relaciona con la energía almacenada en un resonador para una red de segundo orden, uno con dos elementos reactivos de tipos opuestos.
- \(Q\)no está bien definido para redes con tres o más elementos reactivos.
- Sin embargo,\(Q\) es un parámetro de uso frecuente en las ecuaciones de diseño para redes más complejas que las de segundo orden.
- Para redes complejas el\(Q\) se define como la relación de una reactancia a una resistencia cuando se mira en un extremo de la red a una frecuencia. Este valor de no\(Q\) debe utilizarse para deducir el ancho de banda de la red.
- Solo se utiliza (como se define o alguna aproximación del mismo) para guiar el diseño.

