5.5: Terminaciones y Atenuadores

5.5.1 Terminaciones

Las terminaciones se utilizan para absorber completamente una onda que viaja hacia adelante y la característica definitoria es que el coeficiente de reflexión de una terminación es idealmente cero. Si una línea de transmisión tiene una impedancia característica resistiva

Figura\(\PageIndex{1}\): Inductores de chip: (a) inductor en un paquete de montaje en superficie 0603; (b) esquema que muestra tamaños y almohadillas que se proporcionarán en una placa de circuito\((\mathsf{A}=64\text{ mils }(1.63\text{ mm}),\)\( \mathsf{B}=33\text{ mils}\: (0.84\text{ mm}),\)\(\mathsf{C}=24\text{ mils }(0.61\text{ mm}),\)\(\mathsf{D}=13\text{ mils }(0.33\text{ mm}),\)\(\mathsf{E}=30\text{ mils }(0.76\text{ mm}),\)\(\mathsf{F}=25\text{ mils }(0.64\text{ mm}),\)\(G=25\text{ mils }(0.64\text{ mm}),\) y\(\mathsf{H}=40\text{ mils }(1.02\text{ mm)});\) (c) inductor de núcleo de aire de montaje en superficie 0201; y (d) detalle \((\mathsf{A}=23\text{ mils }(0.58\text{ mm}),\)\(\mathsf{B}=18\text{ mils }(0.46\text{ mm}),\)\(\mathsf{C}=17.7\text{ mils }(0.45\text{ mm}),\)\(\mathsf{D}=4\text{ mils }(0.1\text{ mm}),\)\(\mathsf{E}=15\text{ mils }(0.38\text{ mm}),\)\(\mathsf{F}=9\text{ mils }(0.23\text{ mm}),\)\(\mathsf{G}=7\text{ mils }(0.18\text{ mm}),\)y\(\mathsf{H}=18\text{ mils }(0.46\text{ mm}))\). Copyright Coilcraft, Inc., utilizado con permiso [8].

\(L_{\text{nom}}\) \((\text{nH})\)	\(900\text{ MHz}\)		\(1.7\text{ GHz}\)		SRF \((\text{GHz})\)	\(R_{\text{DC}}\) \((\Omega)\)	\(I_{\text{max}}\) \((\text{mA})\)
	\(L\:(\text{nH})\)	\(Q\)	\(L\:(\text{nH})\)	\(Q\)
\ (L_ {\ text {nom}}\)\((\text{nH})\) “>\(0.5\)	\ (900\ texto {MHz}\)\(L\:(\text{nH})\) “>\(0.5\)	\ (900\ texto {MHz}\)\(Q\) “>\(29\)	\ (1.7\ texto {GHz}\)\(L\:(\text{nH})\) “>\(0.49\)	\ (1.7\ texto {GHz}\)\(Q\) “>\(43\)	\ ((\ text {GHz})\) ">\(23.5\)	\ (R_ {\ texto {DC}}\)\((\Omega)\) “>\(0.020\)	\ (I_ {\ text {max}}\)\((\text{mA})\) “>\(1250\)
\ (L_ {\ text {nom}}\)\((\text{nH})\) “>\(1.2\)	\ (900\ texto {MHz}\)\(L\:(\text{nH})\) “>\(1.16\)	\ (900\ texto {MHz}\)\(Q\) “>\(42\)	\ (1.7\ texto {GHz}\)\(L\:(\text{nH})\) “>\(1.16\)	\ (1.7\ texto {GHz}\)\(Q\) “>\(60\)	\ ((\ text {GHz})\) ">\(17.9\)	\ (R_ {\ texto {DC}}\)\((\Omega)\) “>\(0.042\)	\ (I_ {\ text {max}}\)\((\text{mA})\) “>\(870\)
\ (L_ {\ text {nom}}\)\((\text{nH})\) “>\(2.3\)	\ (900\ texto {MHz}\)\(L\:(\text{nH})\) “>\(2.28\)	\ (900\ texto {MHz}\)\(Q\) “>\(45\)	\ (1.7\ texto {GHz}\)\(L\:(\text{nH})\) “>\(2.28\)	\ (1.7\ texto {GHz}\)\(Q\) “>\(64\)	\ ((\ text {GHz})\) ">\(16.5\)	\ (R_ {\ texto {DC}}\)\((\Omega)\) “>\(0.070\)	\ (I_ {\ text {max}}\)\((\text{mA})\) “>\(670\)
\ (L_ {\ text {nom}}\)\((\text{nH})\) “>\(5.2\)	\ (900\ texto {MHz}\)\(L\:(\text{nH})\) “>\(5.21\)	\ (900\ texto {MHz}\)\(Q\) “>\(36\)	\ (1.7\ texto {GHz}\)\(L\:(\text{nH})\) “>\(5.21\)	\ (1.7\ texto {GHz}\)\(Q\) “>\(55\)	\ ((\ text {GHz})\) ">\(10.0\)	\ (R_ {\ texto {DC}}\)\((\Omega)\) “>\(0.170\)	\ (I_ {\ text {max}}\)\((\text{mA})\) “>\(430\)
\ (L_ {\ text {nom}}\)\((\text{nH})\) “>\(9.6\)	\ (900\ texto {MHz}\)\(L\:(\text{nH})\) “>\(9.62\)	\ (900\ texto {MHz}\)\(Q\) “>\(38\)	\ (1.7\ texto {GHz}\)\(L\:(\text{nH})\) “>\(9.64\)	\ (1.7\ texto {GHz}\)\(Q\) “>\(53\)	\ ((\ text {GHz})\) ">\(6.2\)	\ (R_ {\ texto {DC}}\)\((\Omega)\) “>\(0.400\)	\ (I_ {\ text {max}}\)\((\text{mA})\) “>\(280\)
\ (L_ {\ text {nom}}\)\((\text{nH})\) “>\(14.0\)	\ (900\ texto {MHz}\)\(L\:(\text{nH})\) “>\(14.13\)	\ (900\ texto {MHz}\)\(Q\) “>\(37\)	\ (1.7\ texto {GHz}\)\(L\:(\text{nH})\) “>\(14.37\)	\ (1.7\ texto {GHz}\)\(Q\) “>\(51\)	\ ((\ text {GHz})\) ">\(5.1\)	\ (R_ {\ texto {DC}}\)\((\Omega)\) “>\(0.440\)	\ (I_ {\ text {max}}\)\((\text{mA})\) “>\(270\)

Cuadro\(\PageIndex{1}\): Parámetros de los inductores en la Figura\(\PageIndex{1}\) (c). \(L_{\text{nom}}\)es la inductancia nominal, SRF es la frecuencia de autorresonancia, RDC es la resistencia en serie del inductor y\(I_{\text{max}}\) es la corriente RMS máxima soportada.

\(R_{0} = Z_{0}\), luego terminar la línea en una resistencia\(R_{0}\) absorberá completamente la onda que viaja hacia adelante y no habrá reflexión. Entonces se dice que la línea coincide. A frecuencias de RF y microondas se requieren algunos refinamientos a esta simple conexión de circuito. En una línea de transmisión la energía está contenida en los campos EM. Para la línea coaxial, una simple conexión resistiva entre los conductores interno y externo no terminaría los campos y habría cierta reflexión. En cambio, las terminaciones de línea coaxial generalmente comprenden un disco de material resistivo (ver Figura\(\PageIndex{2}\) (a)). La resistencia total del disco desde el conductor interno al externo es la resistencia característica de la línea, sin embargo, el material resistivo se distribuye y así crea una buena terminación de los campos guiados por los conductores coaxiales.

Componente	Símbolo	Alterno
Atenuador fijo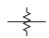
Atenuador, balanceado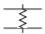
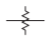Atenuador, desequilibrado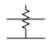
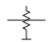Atenuador, variable
Atenuador, continuamente variable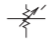
Atenuador, variable escalonada

Tabla\(\PageIndex{2}\): Símbolos estándar IEEE para atenuadores [9].

frecuencias superiores a unos gigahercios. Una terminación de alta calidad se realiza usando una sección de línea con pérdidas como se muestra en la Figura\(\PageIndex{2}\) (b). Aquí el material con pérdida se deposita en la parte superior de una línea de microcinta de circuito abierto. Esto aumenta la pérdida de la línea apreciablemente sin afectar significativamente la impedancia característica de la línea. Si la longitud de la línea con pérdidas es suficientemente larga, digamos una longitud de onda, la onda que viaja hacia adelante será totalmente absorbida y no habrá reflexión. El ahusado del material con pérdidas, como se muestra en la Figura\(\PageIndex{2}\) (b), reduce la discontinuidad entre la línea de microcinta sin pérdidas y la línea con pérdidas al asegurar que parte de la potencia en la onda que viaja hacia adelante se disipa antes de que ocurra el impacto máximo del material con pérdida. Por lo tanto, se logra una terminación coincidente sin el uso de una vía.

5.5.2 Atenuadores

Un atenuador es una red de dos puertos utilizada para reducir la amplitud de una señal y lo hace absorbiendo potencia y sin distorsionar la señal. La entrada y salida del atenuador son ambas coincidentes, por lo que no hay reflejos. Un atenuador puede ser fijo, continuamente variable o discretamente variable. Los símbolos estándar IEEE para atenuadores se muestran en la Tabla\(\PageIndex{2}\). Cuando la atenuación es fija, un atenuador se llama comúnmente almohadilla. Las almohadillas resistivas se pueden utilizar para minimizar el efecto de los pantalones cortos y se abre en

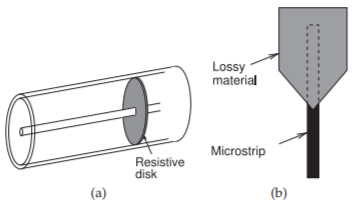
Figura\(\PageIndex{2}\): Terminaciones: (a) terminación resistiva de línea coaxial; (b) carga coincidente de microcinta.

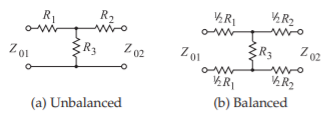
Figura\(\PageIndex{3}\): Atenuador T (Tee). \(K\)es el factor de atenuación (potencia), por ejemplo, un\(3\text{ dB}\) atenuador tiene\(K = 10^{3/10} = 1.995\).

\[\begin{align} R_{1}&=\frac{Z_{01}(K+1)-2\sqrt{KZ_{01}Z_{02}}}{K-1}\quad R_{2}=\frac{Z_{02}(K+1)-2\sqrt{KZ_{01}Z_{02}}}{K-1}\nonumber \\ \label{eq:1}R_{3}&=\frac{2\sqrt{KZ_{01}Z_{02}}}{K-1}\end{align} \]

Si\(Z_{01}=Z_{02}=Z_{0}\), entonces

\[\label{eq:2} R_{1}=R_{2}=Z_{0}\left(\frac{\sqrt{K}-1}{\sqrt{K}+1}\right)\quad\text{and}\quad R_{3}=\frac{2Z_{0}\sqrt{K}}{K-1} \]

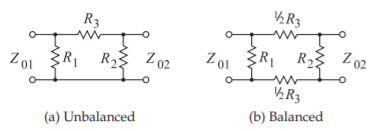
Figura\(\PageIndex{4}\): Atenuador Pi (π). \(K\)es el factor de atenuación (potencia), por ejemplo, un\(20\text{ dB}\) atenuador tiene\(K = 10^{20/10} = 100\).

\[\begin{align} \label{eq:3}R_{1}&=\frac{Z_{01}(K-1)\sqrt{Z_{02}}}{(K+1)\sqrt{Z_{02}}-2\sqrt{KZ_{01}}}\quad R_{2}=\frac{Z_{02}(K-1)\sqrt{Z_{01}}}{(K+1)\sqrt{Z_{01}}-2\sqrt{KZ_{02}}}\\ \label{eq:4}R_{3}&=\frac{(K-1)}{2}\sqrt{\frac{Z_{01}Z_{02}}{K}}\end{align} \]

Si\(Z_{01}=Z_{02}=Z_{0}\), entonces

\[\label{eq:5}R_{1}=R_{2}=Z_{0}\left(\frac{\sqrt{K}+1}{\sqrt{K}-1}\right)\quad\text{and}\quad R_{3}=\frac{Z_{0}(K-1)}{2\sqrt{K}} \]

Si\(R_{1}=R_{2}\), entonces\(Z_{01}=Z_{02}=Z_{0}\)

\[\label{eq:6}Z_{0}=\sqrt{\frac{R_{1}^{2}R_{3}}{2R_{1}+R_{3}}}\quad\text{and}\quad K=\left(\frac{R_{1}+Z_{0}}{R_{1}-Z_{0}}\right)^{2} \]

la integridad de un circuito de RF. Un ejemplo de uso de atenuador en esta situación es en un sistema de TV por cable, donde es crítico que la integridad del sistema no se vea comprometida por un consumidor que desconecte los aparatos de una toma de cable.

Las almohadillas resistivas balanceadas y desequilibradas se muestran en las figuras\(\PageIndex{3}\) y\(\PageIndex{4}\) junto con sus ecuaciones de diseño. Los atenuadores en la Figura\(\PageIndex{3}\) son\(\text{T}\) o\(\text{Tee}\) atenuadores, donde\(Z_{01}\) está la impedancia del sistema a la izquierda de la almohadilla y\(Z_{02}\) es la impedancia del sistema a la derecha de la almohadilla. La característica definitoria es que el coeficiente de reflexión que mira hacia el pad desde la izquierda es cero cuando se hace referencia\(Z_{01}\). Del mismo modo, el coeficiente de reflexión mirando

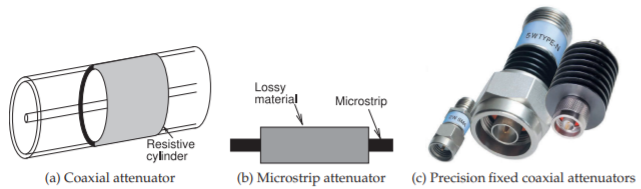
Figura\(\PageIndex{5}\): Atenuadores distribuidos. Los atenuadores en (c) tienen clasificaciones de manejo de potencia de\(2\text{ W},\: 5\text{ W}\) y\(20\text{ W}\) (de izquierda a derecha). Copyright 2012 Scientific Components Corporation d/b/a MiniCircuits, utilizados con permiso [11].

desde la derecha de la almohadilla es cero con respecto a\(Z_{02}\). El factor de atenuación es

\[\label{eq:7}K=\frac{\text{Power in}}{\text{Power out}} \]

En decibelios, la atenuación es

\[\label{eq:8}K|_{\text{dB}}=10\log_{10}K=(\text{Power in})|_{\text{dBm}}-(\text{Power out})|_{\text{dBm}} \]

Si las impedancias izquierda y derecha del sistema son diferentes, entonces hay un factor de atenuación mínimo que se puede lograr [10]:

\[\label{eq:9}K_{\text{MIN}}=\left\{\begin{array}{ll}{\left[2Z_{01}-Z_{02}+2\sqrt{Z_{01}(Z_{01}-Z_{02})}\right]/Z_{02},}&{Z_{01}\geq Z_{02}}\\{\left[2Z_{02}-Z_{01}+2\sqrt{Z_{02}(Z_{02}-Z_{01})}\right]/Z_{01},}&{Z_{01}\leq Z_{02}}\end{array}\right. \]

Esta limitación viene del requisito simultáneo de que el pad sea emparejado. Si hay una sola impedancia del sistema\(Z_{0} = Z_{01} = Z_{02}\), entonces\(K_{\text{MIN}} = 1\), y así se puede obtener cualquier valor de atenuación.

Los atenuadores agrupados son útiles hasta 10 GHz por encima de los cuales el tamaño de los elementos resistivos se vuelve grande en comparación con una longitud de onda. Además, para los circuitos planos, se requieren vías, y éstas no son deseables desde el punto de vista de la fabricación, y eléctricamente tienen una inductancia pequeña. Afortunadamente, los atenuadores se pueden realizar usando una sección con pérdidas de la línea de transmisión, como se muestra en la Figura\(\PageIndex{5}\). Aquí, el material con pérdida da como resultado una sección de línea con una constante de atenuación alta. Generalmente el material con pérdida tiene poco efecto sobre la impedancia característica de la línea, por lo que hay poca reflexión en la entrada y salida del atenuador. Los atenuadores distribuidos se pueden usar a frecuencias más altas que los atenuadores de elementos agrupados, y se pueden realizar con cualquier estructura de línea de transmisión.

Otro ejemplo del uso de atenuadores en la combinación de la salida de dos fuentes se muestra en la Figura\(\PageIndex{6}\). Esta es una situación común en las mediciones donde se van a combinar las salidas de dos fuentes de instrumentación. Los atenuadores reducen el nivel de la señal presentada a la salida de una fuente por la otra. Si el nivel de la segunda señal es alto, la mayoría de las fuentes producirían distorsión no lineal, incluyendo productos de mezcla no lineales.

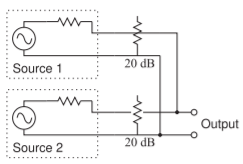
Figura\(\PageIndex{6}\): El uso de atenuadores para aislar las salidas de dos fuentes que se combinan.

Ejemplo\(\PageIndex{1}\): Pad Design

Diseñar una\(20\text{ dB}\) almohadilla desequilibrada en un\(75\:\Omega\) sistema.

Solución

Hay dos diseños posibles que utilizan almohadillas resistivas. Estas son las almohadillas de Tee y Pi desequilibradas que se muestran en las Figuras\(\PageIndex{3}\) y\(\PageIndex{4}\). Se elegirá el diseño Tee. El\(K\) factor es

\[\label{eq:10}K=10^{(K|_{\text{dB}}/10)} = 10^{(20/10)} = 100 \]

Desde\(Z_{01} = Z_{02} = 75\:\Omega\), Ecuación\(\eqref{eq:2}\) rinde

\[\begin{align}\label{eq:11}R_{1}&=R_{2}=75\left(\frac{\sqrt{100}-1}{\sqrt{100}+1}\right)=75\left(\frac{9}{11}\right)=61.4\:\Omega \\ \label{eq:12}R_{3}&=\frac{2\cdot 75\sqrt{100}}{100-1}=150\left(\frac{10}{99}\right)=15.2\:\Omega\end{align} \]

El diseño final es

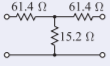
Figura\(\PageIndex{7}\)