5.6: Tomas y discontinuidades de línea de transmisión

Las interrupciones del campo magnético o eléctrico crean regiones donde se almacena energía magnética adicional o energía eléctrica. Si la energía adicional almacenada es predominantemente magnética, la discontinuidad introducirá una inductancia. Si la energía adicional almacenada es predominantemente eléctrica, la discontinuidad introducirá una capacitancia. Tales discontinuidades ocurren con todas las líneas de transmisión. En algunos casos, las discontinuidades de las líneas de transmisión introducen parásitos no deseados, pero también brindan la oportunidad de introducir efectivamente componentes de elementos grumosos. En esta sección se considerarán discontinuidades de microcinta, pero los principios se aplican a todas las estructuras de líneas de transmisión. El elemento de circuito de microondas más simple es una sección uniforme de la línea de transmisión que se puede utilizar para introducir un retardo de tiempo o un desplazamiento de fase dependiente de la frecuencia. Más comúnmente se usa para interconectar otros componentes. Los segmentos de línea, incluidos los codos y los cruces, se muestran en la Figura\(\PageIndex{1}\).

5.6.1 Abierto

Muchas discontinuidades de líneas de transmisión surgen de campos de franjas. Un elemento es la microcinta abierta, mostrada en la Figura\(\PageIndex{2}\). Los campos de franjas al final de la línea de transmisión en la Figura\(\PageIndex{2}\) (a) almacenan energía en el campo eléctrico, y ésta puede modelarse por la capacitancia de franja\(C_{F}\), mostrada en la Figura\(\PageIndex{2}\) (b). Este efecto también puede modelarse mediante una línea de transmisión extendida, como se muestra en la Figura\(\PageIndex{2}\) (c). Para una línea típica de microcinta con\(\varepsilon_{r} = 9.6,\: h = 600\:\mu\text{m},\) y\(w/h = 1,\)\(C_{F}\) es aproximadamente\(36\text{ fF}\). Sin embargo,\(C_{F}\) varía con la frecuencia, y la longitud extendida es una aproximación mucho mejor al efecto de la franja [12]. Para las mismas dimensiones, la longitud de la extensión es aproximadamente\(0.35h\) y casi independiente de la frecuencia [13]. Al igual que con muchos efectos de franja, se puede utilizar una capacitancia o inductancia para modelar el efecto de la franja, pero generalmente un modelo distribuido es mejor.

5.6.2 Discontinuidades

Varias discontinuidades de microcinta y sus circuitos equivalentes se muestran en la Figura\(\PageIndex{3}\). Las discontinuidades (Figura\(\PageIndex{3}\) (b—g)) son modeladas por elementos capacitivos si el\(E\) campo se ve afectado y por elementos inductivos si el\(H\) campo (o corriente) está perturbado. El stub mostrado en la Figura\(\PageIndex{3}\) (b), por ejemplo, se modela mejor usando elementos agrupados que describen la unión así como la línea de transmisión del propio trozo. Los racimos actuales en ángulo recto se doblan desde la línea pasante hasta el talón. El agrupamiento de corriente conduce a que el exceso de energía se almacene en el campo magnético y, por lo tanto, un efecto inductivo. También hay exceso de almacenamiento de carga en la región de placa paralela delimitada por las líneas a través de la izquierda y la derecha y el talón. Esto es modelado por una capacitancia.

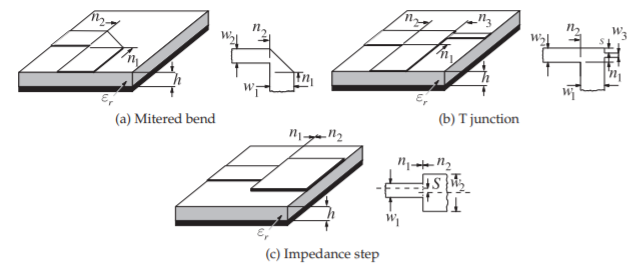
Figura\(\PageIndex{1}\): Discontinuidades de microcinta.

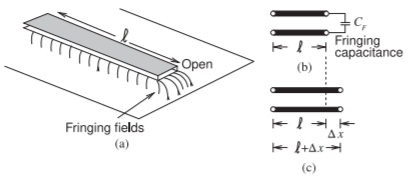
Figura\(\PageIndex{2}\): Un abierto en una línea de transmisión de microcinta: (a) línea de microcinta que muestra campos de franqueo al aire libre; (b) modelo de capacitancia de franjas del abierto; y (c) un modelo de línea extendida del abierto\(\Delta x\) siendo la longitud de línea de transmisión adicional que captura el abierto.

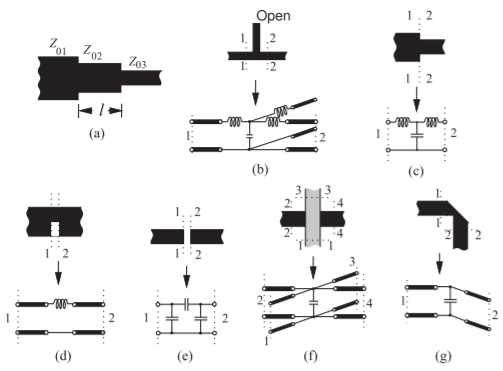
Figura\(\PageIndex{3}\): Discontinuidades de microbanda: (a) transformador de impedancia de cuarto de onda; (b) trozo abierto de microcinta; (c) escalón; (d) muesca; (e) hueco; (f) cruce; y (g) curva.

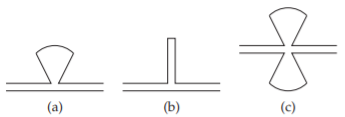
Figura\(\PageIndex{4}\): Tambones de microbanda: (a) trozo conectado a derivación radial; (b) trozo de derivación convencional; y (c) trozo radial mariposa.

5.6.3 Transformador de impedancia

Los transformadores de impedancia interconectan dos líneas de diferente impedancia característica. La transición más suave y la que tiene el ancho de banda más amplio es una línea cónica. Este elemento puede ser largo y luego se utiliza a veces un transformador de impedancia de cuarto de onda\(\PageIndex{3}\) (ver Figura (a)), aunque su ancho de banda es relativamente pequeño y centrado en la frecuencia a la que\(l = \lambda_{g}/4\). Idealmente\(Z_{0,2} =\sqrt{Z_{0,1}Z_{0,3}}\). Este tema se considera más a fondo en la Sección 7.5 donde se considera en detalle el diseño de líneas cónicas y transformadores multietapa de cuarto de onda.

5.6.4 Talón radial plano

El uso de un trozo radial (Figura\(\PageIndex{4}\) (a)), a diferencia del trozo de microcinta convencional (Figura\(\PageIndex{4}\) (b)), puede mejorar el ancho de banda de muchos circuitos de microcinta. Una ventaja importante de un trozo radial es que la impedancia de entrada presentada a la línea pasante generalmente tiene un ancho de banda más amplio que el obtenido con el stub convencional. Cuando se introducen dos talones radiales conectados en derivación en paralelo (es decir, uno a cada lado de la línea de alimentación de microcinta) la configuración resultante se denomina un trozo de “mariposa” (ver Figura\(\PageIndex{4}\) (c)). Los parámetros críticos de diseño incluyen el radio y el ángulo del trozo.\(r\)

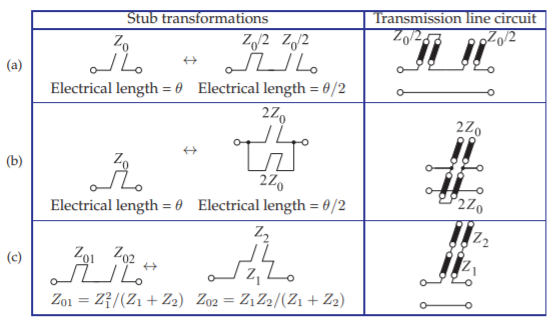
Figura\(\PageIndex{5}\): Transformaciones de red stub: (a) stubs abiertos y (b) cortocircuitados después de la aplicación de la transformada de medio ángulo [14]; y (c) equivalencia entre conexión en serie de stubs abiertos y cortocircuitados y línea de transmisión de impedancia escalonada.

5.6.5 Transformaciones de Stub

Las transformaciones de stub en la Figura\(\PageIndex{5}\) permiten reducir las longitudes de los stubs. Las dos primeras transformaciones stub (Figura\(\PageIndex{5}\) (a y b)) se denominan transformaciones de medio ángulo y permiten que un stub sea reemplazado por dos stubs más cortos. La tercera transformación stub (Figura\(\PageIndex{5}\) (c)) permite que dos stubs sean reemplazados por dos líneas de transmisión en cascada.

La Figura\(\PageIndex{5}\) (a) es una transformación de medio ángulo de un trozo de circuito abierto en serie. Matemáticamente la transformación se describe de la siguiente manera. Considere la impedancia de entrada de un trozo de circuito abierto [14] con longitud eléctrica\(\theta = \beta\ell\) en frecuencia\(f\) y que es un cuarto de longitud de onda de largo a\(f_{0}\) (es decir,\(\theta = \pi/2\) at\(f_{0}\)) (de la Sección 2.4.4 de [15] y usando la Ecuación ((1.105)) de [15]):

\[\label{eq:1} Z_{oc}=-\jmath Z_{0}\cot (\theta )=\jmath (Z_{0}/2)\tan(\theta/2)-\jmath (Z_{0}/2)\tan(\theta /2) \]

En general,\(\theta = (\pi /2)\)\((f/f_{0})\). El lado derecho de la ecuación\(\eqref{eq:1}\) describe la conexión en serie de stubs cortos y de circuito abierto que tienen impedancias características de\(Z_{0}/2\) y la mitad de la longitud eléctrica original. Esto implica que los resonadores de línea de transmisión resultantes tienen un cuarto de longitud de onda\(2f_{0}\) (es decir, tienen un octavo de longitud de onda\(f_{0}\)). La transformación de medio ángulo se aplica a todas las frecuencias y no solo a las frecuencias cercanas\(f_{0}\). Mediante un tratamiento analítico similar, el trozo cortocircuitado tiene la equivalencia mostrada en la Figura\(\PageIndex{5}\) (b). El trozo cortocircuitado en serie a la izquierda en la Figura\(\PageIndex{5}\) (b) tiene la admisión en serie

\[\label{eq:2}Y_{T}=\frac{1}{\jmath Z_{0}\tan(\theta )}=\frac{1}{\jmath Z_{0}}\cot (\theta ) \]

y los stubs en la transformación tienen una impedancia de entrada

\[\label{eq:3}Z_{oc}=-\jmath\frac{1}{2}Z_{0}\cot(\theta /2)\quad\text{and}\quad Z_{sc}=\jmath\frac{1}{2}Z_{0}\tan(\theta /2) \]

Estos stubs están en paralelo para que la admitancia total de entrada sea

\[\begin{align}Y_{T}&=\frac{1}{Z_{oc}}+\frac{1}{Z_{sc}}=\frac{2}{-\jmath Z_{0}\cot(\theta /2)}+\frac{1}{\jmath Z_{0}\tan (\theta /2)}\nonumber \\ \label{eq:4} &=\frac{2}{\jmath Z_{0}}\left[-\tan(\theta /2)+\cot (\theta /2)\right]=\frac{1}{\jmath Z_{0}}\cot(\theta )\end{align} \]

Examinando las Ecuaciones\(\eqref{eq:2}\) y\(\eqref{eq:4}\) se ve que son idénticas, por lo que la Figura\(\PageIndex{5}\) (b) representa otra transformación de medio ángulo.

Para los stubs abiertos y cortocircuitados en serie de la Figura\(\PageIndex{5}\) (c), las impedancias de entrada de los stubs abiertos y cortocircuitados son

\[\label{eq:5}Z_{oc}=-\jmath Z_{02}\cot(\theta)\quad\text{and}\quad Z_{sc}=\jmath Z_{01}\tan(\theta ) \]

respectivamente, de manera que la impedancia total de la serie es

\[\label{eq:6}Z_{T}=Z_{oc}+Z_{sc}=-\jmath Z_{02}\cot (\theta)+\jmath Z_{01}\tan (\theta) \]

Para la transformación de la derecha, la impedancia que busca en el trozo de circuito abierto (exterior) es

\[\label{eq:7}Z_{x}=-\jmath Z_{2}\cot (\theta) \]

y la impedancia total es

\[\label{eq:8}Z_{T}=Z_{1}\left[\frac{−\jmath Z_{2} \cot(\theta) + \jmath Z_{1} \tan(\theta )}{Z_{1} + Z_{2} \cot(\theta )\tan(\theta )}\right]=\frac{−\jmath Z_{1}Z_{2} \cot(\theta )}{Z_{1}+Z_{2}}+\frac{\jmath Z_{1}^{2}\tan(\theta)}{Z_{1}+Z_{2}} \]

Ecuación de Ecuaciones\(\eqref{eq:6}\) y\(\eqref{eq:8}\) y recopilación de términos,

\[\label{eq:9}Z_{02}=Z_{1}Z_{2}/(Z_{1}+Z_{2})\quad\text{and}\quad Z_{01}=Z_{1}^{2}/(Z_{1}+Z_{2}) \]

y los segmentos de línea de transmisión (de impedancia característica\(Z_{01},\: Z_{02},\: Z_{1}\) y\(Z_{2}\)) todos tienen la misma longitud eléctrica.

En resumen, las transformaciones de stub se mantienen sin importar la longitud de los talones. Las transformaciones de segmento de medio ángulo permiten miniaturizar los circuitos de línea de transmisión.