5.7: Resonadores
- Page ID
- 80795
Cerca de la resonancia, la respuesta de un resonador de microondas es muy similar a la respuesta de resonancia de un circuito\(LC\) resonante paralelo o en serie, mostrado en la Figura\(\PageIndex{1}\) (e y f). Estos circuitos equivalentes se pueden usar en un rango de frecuencia estrecho de quizás ancho de banda\(5\%\) fraccional.
En la Figura se muestran varios tipos de resonadores\(\PageIndex{1}\). La Figura\(\PageIndex{1}\) (a) es un resonador de cavidad rectangular acoplado a una línea coaxial externa mediante un pequeño bucle de acoplamiento. La Figura\(\PageIndex{1}\) (b) es un resonador de reflexión de parche de microcinta. Este resonador tiene un acoplamiento grande al circuito externo. El acoplamiento se puede reducir y controlar fotolitográficamente mediante la introducción de un hueco, como se muestra en la Figura\(\PageIndex{1}\) (c), para crear lo que se llama un resonador de reflexión de línea de transmisión acoplada a microbanda. El\(Q\) de un resonador se puede aumentar drásticamente mediante el uso de un material de baja pérdida y alta constante dieléctrica, como se muestra en la Figura\(\PageIndex{1}\) (d), para un resonador de transmisión dieléctrica en microcinta.
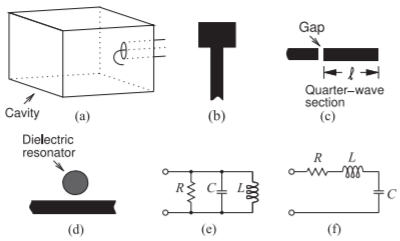
Figura\(\PageIndex{1}\): Resonadores de microondas: (a) resonador de cavidad rectangular, (b) resonador de parche de microcinta (c) resonador de reflexión acoplado a microcinta, (d) resonador de transmisión dieléctrica en microcinta, (e) circuitos equivalentes paralelos y (f) circuitos equivalentes en serie.
5.7.1 Resonadores dieléctricos
Cualquier estructura dieléctrica puede almacenar energía EM, con la frecuencia resonante dependiente tanto de la permitividad como de las dimensiones físicas. A la frecuencia de resonancia, todos los resonadores almacenan la cantidad máxima de energía. Dos resonadores que almacenan cantidades particularmente grandes de energía son el resonador de cavidad mostrado en la Figura\(\PageIndex{1}\) (a) y el resonador dieléctrico mostrado en la Figura\(\PageIndex{1}\) (d).
Las cerámicas de microondas pueden tener pérdidas muy bajas y alta permitividad (lo que da como resultado longitudes de onda pequeñas y, por lo tanto, un tamaño pequeño) y se usan comúnmente en resonadores de microondas. Los materiales cerámicos de baja pérdida con permitividades en el rango de\(21\) a\(150\) están generalmente disponibles y\(Q\) los factores descargados están en el\(10,000\) rango\(5,000\) a. Las dimensiones físicas generalmente dependen de las frecuencias resonantes deseadas.
La expresión teórica general para las frecuencias resonantes, aplicada a un resonador dieléctrico cilíndrico de radio\(a\) y altura\(d\), es
\[\label{eq:1}f_{mnl}=\frac{c}{2\sqrt{\varepsilon_{r}}}\sqrt{\left(\frac{χ_{mn}}{\pi a}\right)^{2}+\left(\frac{l}{d}\right)^{2}} \]
donde el número entero\(l\) denota el número de medias longitudes de onda en la dirección vertical y\(χ_{mn}\) es el extremo\(m\) th de la función de Bessel\(J_{n}\) para un modo TM (o alternativamente el\(m\) ésimo cero para un modo TE).
La Figura\(\PageIndex{1}\) (d) muestra un uso común de un resonador dieléctrico, a menudo llamado un puck, acoplándose a los campos de una línea de microcinta. El puck tiene una resonancia definida por el radio del puck de alta permitividad. Puede haber varios modos de resonancia, con algunos modos introduciendo un circuito resonante paralelo (Figura\(\PageIndex{1}\) (e)) en derivación a través de la línea y otros introduciendo un circuito resonante en serie en derivación a través de la línea (Figura\(\PageIndex{1}\) (f)).

