6.12: Ejercicios

1. Considere el diseño de un transformador magnético que haga coincidir la resistencia de\(3\:\Omega\) salida de un amplificador de potencia (esta es la fuente) a una\(50\:\Omega\) carga. El secundario del transformador está en el lado de carga.
   1. ¿Cuál es la relación entre el número de giros primarios y el número de giros secundarios para una coincidencia ideal?
   2. Si la relación del transformador pudiera implementarse exactamente (la situación ideal), ¿cuál es el coeficiente de reflexión normalizado para\(3\:\Omega\) buscar en el primario del transformador con la\(50\:\Omega\) carga?
   3. ¿Cuál es la pérdida de retorno ideal del transformador cargado (mirando al primario)? Exprese su respuesta en\(\text{dB}\).
   4. Si hay devanados\(100\) secundarios, ¿cuántos devanados primarios hay en su diseño? Tenga en cuenta que el número de devanados debe ser un número entero. (Esta situación práctica será considerada en el resto del problema.)
   5. ¿Cuál es la resistencia de entrada del transformador que mira hacia el primario?
   6. ¿Cuál es el coeficiente de reflexión normalizado para\(3\:\Omega\) buscar en el primario del transformador con la\(50\:\Omega\) carga?
   7. ¿Cuál es la pérdida de retorno real (in\(\text{dB}\)) del transformador cargado (mirando al primario)?
   8. Si la potencia máxima disponible del amplificador es\(20\text{ dBm}\), ¿cuánta potencia (in\(\text{dBm}\)) se refleja en la entrada del transformador?
   9. Así, ¿cuánta energía (in\(\text{dBm}\)) se entrega a la carga ignorando la pérdida en el transformador?
2. Considera el diseño de un transformador magnético que coincidirá con una resistencia de\(50\:\Omega\) salida a la\(100\:\Omega\) carga que presenta un amplificador. El secundario del transformador está en el lado de carga (amplificador).
   1. ¿Cuál es la relación entre el número de giros primarios y el número de giros secundarios para una coincidencia ideal?
   2. Si la relación del transformador pudiera implementarse exactamente (la situación ideal), ¿cuál es el coeficiente de reflexión normalizado para\(50\:\Omega\) buscar en el primario del transformador con la carga?
   3. ¿Cuál es la pérdida de retorno ideal del transformador cargado (mirando al primario)? Exprese su respuesta en\(\text{dB}\).
   4. Si hay devanados\(20\) secundarios, ¿cuántos devanados primarios hay en su diseño? Tenga en cuenta que el número de devanados debe ser un número entero? (Esta situación será considerada en el resto del problema.)
   5. ¿Cuál es la resistencia de entrada del transformador que mira hacia el primario?
   6. ¿Cuál es el coeficiente de reflexión normalizado para\(50\:\Omega\) investigar el primario del transformador cargado?
   7. ¿Cuál es la pérdida de retorno real (in\(\text{dB}\)) del transformador cargado (mirando al primario)?
   8. Si la potencia máxima disponible de la fuente es\(−10\text{ dBm}\), ¿cuánta energía (in\(\text{dBm}\)) se refleja de la entrada del transformador?
   9. Así, ¿cuánta potencia (in\(\text{dBm}\)) se entrega al amplificador ignorando la pérdida en el transformador?
3. Considere el diseño de una red\(\text{L}\) -matching centrada en\(1\text{ GHz}\) que coincidirá la resistencia de\(2\:\Omega\) salida de un amplificador de potencia (esta es la fuente) a una\(50\:\Omega\) carga. [Ejemplo de Parallels 6.4.1 pero tenga en cuenta el requisito de bloqueo de CC a continuación.]
   1. ¿Cuál es el\(Q\) de la red de emparejamiento?
   2. La red coincidente debe bloquear la corriente CC. Dibujar la topología de la red coincidente.
   3. ¿Cuál es la reactancia del elemento serie en la red coincidente?
   4. ¿Cuál es la reactancia del elemento shunt en la red coincidente?
   5. ¿Cuál es el valor del elemento serie en la red coincidente?
   6. ¿Cuál es el valor del elemento shunt en la red coincidente?
   7. Dibuje y etiquete el diseño final de su red correspondiente, incluidas las resistencias de origen y carga.
   8. Aproximadamente, ¿cuál es el\(3\text{ dB}\) ancho de banda de la red coincidente?
4. Considere el diseño de una red\(\text{L}\) -matching centrada en\(100\text{ GHz}\) que coincidirá una fuente con una resistencia Thevenin de\(50\:\Omega\) a la entrada de un amplificador que presenta una resistencia de carga de\(100\:\Omega\) a la red coincidente. [Ejemplo de Parallels 6.4.2 pero tenga en cuenta el requisito de bloqueo de CC a continuación.]
   1. ¿Cuál es el\(Q\) de la red de emparejamiento?
   2. La red coincidente debe bloquear la corriente CC. Dibujar la topología de la red coincidente.
   3. ¿Cuál es la reactancia del elemento serie en la red coincidente?
   4. ¿Cuál es la reactancia del elemento shunt en la red coincidente?
   5. ¿Cuál es el valor del elemento serie en la red coincidente?
   6. ¿Cuál es el valor del elemento shunt en la red coincidente?
   7. Dibuje y etiquete el diseño final de su red correspondiente, incluyendo la fuente y la resistencia a la carga.
   8. Aproximadamente, ¿cuál es el\(3\text{ dB}\) ancho de banda de la red coincidente?
5. Diseñe una red Pi para que coincida con la configuración de origen con la configuración de carga a continuación. La frecuencia de diseño es\(900\text{ MHz}\) y la deseada\(Q\) es\(10\). [Ejemplo de Parallels 6.6.2]

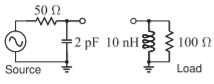
Figura\(\PageIndex{1}\)

6. Diseñe una red Pi para que coincida con la configuración de origen con la configuración de carga a continuación. La frecuencia de diseño es\(900\text{ MHz}\) y la deseada\(Q\) es\(10\). [Ejemplo de Parallels 6.6.2]

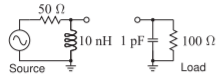
Figura\(\PageIndex{2}\)

7. Desarrollar el diseño eléctrico de una red\(\text{L}\) -matching para hacer coincidir la fuente con la carga a continuación.

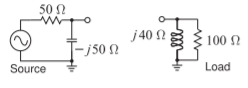
Figura\(\PageIndex{3}\)

8. Desarrollar el diseño eléctrico de una red\(\text{L}\) -matching para hacer coincidir la fuente con la carga a continuación.

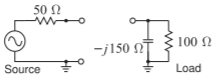
Figura\(\PageIndex{4}\)

9. Diseñe una red de coincidencia de elementos de paso bajo para que coincida con la fuente y la carga que se muestran a continuación. La frecuencia de diseño es\(1\text{ GHz}\). Debes usar un Smith Chart y mostrar claramente tu trabajo y derivaciones. Se deben desarrollar los valores finales de los elementos.

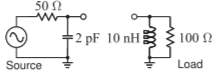
Figura\(\PageIndex{5}\)

10. Considere el diseño de una red\(\text{L}\) -matching centrada en\(100\text{ GHz}\) que coincidirá una fuente con una resistencia Thevenin de\(50\:\Omega\) a la entrada de un amplificador que presenta una resistencia de carga de\(200\:\Omega\) a la red coincidente. [Ejemplo de Parallels 6.4.2 pero tenga en cuenta el requisito de bloqueo de CC a continuación.]
    1. ¿Cuál es el\(Q\) de la red de emparejamiento?
    2. La red coincidente debe bloquear la corriente CC. Dibujar la topología de la red coincidente.
    3. ¿Cuál es la reactancia del elemento serie en la red coincidente?
    4. ¿Cuál es la reactancia del elemento shunt en la red coincidente?
    5. ¿Cuál es el valor del elemento serie en la red coincidente?
    6. ¿Cuál es el valor del elemento shunt en la red coincidente?
    7. Dibuje y etiquete el diseño final de su red correspondiente, incluyendo la fuente y la resistencia a la carga.
    8. Aproximadamente, ¿cuál es el\(3\text{ dB}\) ancho de banda de la red coincidente?
11. Considere el diseño de la red de coincidencia de salida de un amplificador de\(15\text{ GHz}\) señal pequeña. El amplificador consiste en un activo de dos puertos y redes de coincidencia de entrada y salida. Port\(\mathsf{1}\) es la entrada del dispositivo activo y Port\(\mathsf{2}\) es su salida, y sus\(50\:\Omega\: S\) parámetros son\(S_{11} = 0.5\angle 45^{\circ},\: S_{12} = 0.1\angle 0^{\circ},\: S_{21} = 2\angle 90^{\circ},\) y\(S_{22} = 0.75\angle − 45^{\circ}\).
    1. Si la entrada del dispositivo activo se termina en\(50\:\Omega\), ¿cuál es la impedancia que busca en la salida del amplificador?
    2. Diseñe una red de coincidencia de elementos agrupados de dos elementos para una máxima transferencia de potencia desde la salida del transistor a una\(50\:\Omega\) carga. Desarrollar al menos dos diseños y compararlos. (Tenga en cuenta que la salida del dispositivo activo aparece físicamente como una resistencia en paralelo con una capacitancia y esto se puede usar para contrastar sus diseños).
12. Desarrolle una red coincidente de dos elementos para la configuración de fuente/carga que se muestra en la siguiente figura. La red coincidente debe pasar DC. La frecuencia central de la red coincidente es\(f = 1\text{ GHz}\). Hay una serie de consideraciones de diseño que deben considerarse antes de embarcarse en la síntesis de redes.

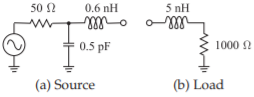
Figura\(\PageIndex{6}\)

Considera lo siguiente:

1. La fuente necesita ser colapsada a un circuito equivalente con una resistencia y una reactancia.
2. Los elementos reactivos en la fuente y la carga se acomodarán mediante absorción o resonancia. Se prefiere la absorción, pero no siempre es posible.
3. Los requisitos de CC requieren una red de coincidencia de paso bajo. Por lo que debe haber una inductancia en serie y un condensador de derivación en la red coincidente. Dado que la resistencia de carga es mayor que la resistencia de la fuente, el diseño más probable tiene un condensador de derivación en el lado de la carga. Sin embargo, esto puede cambiar cuando se consideran las propiedades de transformación de las reactancias de fuente y carga.
4. La reactancia de la fuente debe ser manejada por un inductor en serie o un condensador de derivación. Se debe considerar la impedancia de entrada de la fuente para determinar cuál.
5. La reactancia de carga será resonada por un condensador de derivación. Parece que la absorción será una posibilidad en la carga.

1. ¿Cuál es la impedancia de entrada de la fuente? Trate el generador de voltaje como un cortocircuito.
2. ¿Cuál es la reactancia del elemento serie que resonará la reactancia efectiva de entrada de la fuente?
3. ¿Cuál es la entrada de entrada de la carga?
4. ¿Cuál es la reactancia de derivación requerida para resonar la carga?
5. ¿Cuál es el problema del emparejamiento resistivo? Es decir, dado que las reactancias de la carga y la fuente han sido resonadas por consideración, cuáles son las resistencias efectivas de fuente y carga. Derivar la red de coincidencia requerida. Mantener los valores de los elementos de la red coincidente como reactancias.
6. Dibuje la red de coincidencia completa que muestre los elementos de fuente y carga requeridos para la resonancia, así como la red coincidente para el problema resistivo. Mantener los valores de los elementos como reactancias.
7. Dibuja la red de coincidencia final combinando todos los elementos resonantes y coincidentes. Mantener los valores de los elementos como reactancias. Este es el diseño eléctrico de la red coincidente.
8. Calcular los valores de inductancia y capacitancia de la red coincidente.

13. Diseñe una red coincidente de dos elementos para interconectar una fuente con una impedancia equivalente\(25\:\Omega\) Thevenin a una carga que consiste en un condensador en paralelo con una resistencia para que la admitancia de carga sea\(Y_{L} = 0.02 +\jmath 0.02\: S\). Utilice el método de absorción para manejar la carga reactiva.
14. Diseñe una red coincidente para interconectar una fuente con una impedancia equivalente\(25\:\Omega\) Thevenin a una carga que consiste en un condensador en paralelo con una resistencia para que la admitancia de carga sea\(Y_{L} = 0.01 +\jmath 0.01\: S\).
    1. Si no se limita la complejidad de la red coincidente, ¿cuál es el mínimo\(Q\) que se podría lograr en la red completa que consiste en la red coincidente y las impedancias de origen y carga?
    2. Esbozar el procedimiento para diseñar la red coincidente para el ancho de banda máximo si solo se pueden usar cuatro elementos en la red. No es necesario diseñar la red.
15. Diseñe una red de coincidencia de elementos agrupados para que coincida con una fuente, con una impedancia equivalente a Thevenin de\(50\:\Omega\), a una carga que consiste en una\(100\:\Omega\) resistencia en paralelo con un\(5\text{ pF}\) condensador. Diseñe la red coincidente para obtener el ancho de banda máximo al\(1\text{ GHz}\) usar no más de cuatro elementos agrupados.
    1. ¿Cuántos elementos hay en la red coincidente?
    2. Esboza cómo diseñarás la red coincidente.
    3. Diseñar la red coincidente. Debe dibujar el diseño final, incluidos los elementos de origen y carga, y etiquetar cada uno de los elementos agrupados usando valores de reactancia. (Es decir, no calcule valores de la inductancia y capacitancias en su diseño). (No utilice un gráfico Smith.)
16. La salida de un amplificador de transistor se modela como una fuente de corriente en paralelo con una\(50\:\Omega\) resistencia y un\(1\text{ pF}\) condensador. Esto se debe hacer coincidir con una carga que consiste en una\(25\:\Omega\) resistencia en serie con un\(0.02\text{ nH}\) inductor. La tarea es diseñar una red coincidente que permita aplicar polarización de CC desde la carga a la salida del transistor, por lo que la red coincidente debe ser de tipo paso bajo. La frecuencia central del sistema es\(10\text{ GHz}\) y\(50\text{ MHz}\) se requiere un ancho de banda de.
    1. ¿Cuál es el ancho de banda fraccional del sistema?
    2. ¿Cuál es el\(Q\) del sistema?
    3. Indique la forma de la red coincidente si no se van a utilizar más de cuatro elementos reactivos; es decir, esbozar la red coincidente.
    4. Completar el diseño del amplificador proporcionando valores numéricos de elementos.
17. Diseñe una red Pi para que coincida con la configuración de origen con la configuración de carga a continuación. La frecuencia de diseño es\(900\text{ MHz}\) y la deseada\(Q\) es\(10\).

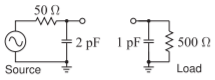
Figura\(\PageIndex{7}\)

18. Diseñe una red de adaptación pasiva que logre la máxima coincidencia de ancho de banda desde una fuente con una impedancia de\(2\:\Omega\) (típica de la impedancia de salida de un amplificador de potencia) a una carga con una impedancia de\(50\:\Omega\). La red coincidente puede tener un máximo de tres elementos reactivos. Solo necesita calcular las reactancias y no los valores del condensador y del inductor.
19. Diseñe una red de adaptación pasiva que logre la máxima coincidencia de ancho de banda de una fuente con una impedancia de\(20\:\Omega\) a una carga con una impedancia de\(125\:\Omega\). La red coincidente puede tener un máximo de cuatro elementos reactivos. Solo necesita calcular las reactancias y no los valores del condensador y del inductor.
    1. ¿Utilizará dos, tres o cuatro elementos en su red coincidente?
    2. Con un diagrama, y quizás ecuaciones, indican el procedimiento de diseño.
    3. Diseñar la red coincidente. Es suficiente usar valores de reactancia.
20. Diseñe una red de adaptación pasiva que logre la máxima coincidencia de ancho de banda de una fuente con una impedancia de\(60\:\Omega\) a una carga con una impedancia de\(5\:\Omega\). La red coincidente puede tener un máximo de cuatro elementos reactivos. Solo necesita calcular las reactancias y no los valores del condensador y del inductor.
    1. ¿Utilizará dos, tres o cuatro elementos en su red coincidente?
    2. Con un diagrama y quizás ecuaciones, indicar el procedimiento de diseño.
    3. Diseñar la red coincidente. Es suficiente usar valores de reactancia.
21. Diseñe una\(\text{T}\) red para hacer coincidir una\(50\:\Omega\) fuente con una\(1000\:\Omega\) carga. El cargado deseado\(Q\) es\(15\).
22. Repita el Ejemplo 6.3.2 con un inductor en serie con la carga. Mostrar que la inductancia se puede ajustar para obtener cualquier valor de resistencia de derivación positiva.
23. Diseñe una red de adaptación de tres elementos agrupados que interconecte una fuente con una impedancia de\(5\:\Omega\) a una carga con una impedancia que consiste en una resistencia con una impedancia de\(10\:\Omega\). La red debe tener un\(Q\) de\(6\).
24. Una fuente con una impedancia equivalente a Thevenin de\(75\:\Omega\) debe impulsar una carga con una impedancia de\(5\:\Omega\). Se debe diseñar una red coincidente con el máximo ancho de banda posible entre la fuente y la carga para lograr la máxima transferencia de potencia. Diseñe la red coincidente para obtener el máximo ancho de banda posible utilizando no más de cuatro elementos reactivos.
    1. Dibuje el esquema de la red coincidente.
    2. Describir el procedimiento de diseño.
    3. Completar el diseño de la red coincidente. Determinar los valores de los elementos si la frecuencia central es\(1\text{ GHz}\).
25. A continuación se muestra una red coincidente de dos puertos con un generador y una carga. La impedancia del generador es de 40 Ω y la impedancia de carga es\(Z_{L} = 50 −\jmath 20\:\Omega\). Utilice un gráfico de Smith para diseñar la red coincidente.

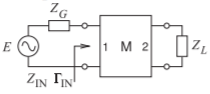
Figura\(\PageIndex{8}\)

1. ¿Cuál es la condición para la transferencia máxima de potencia desde el generador? Exprese su respuesta usando impedancias.
2. ¿Cuál es la condición para la transferencia máxima de potencia desde el generador? Exprese su respuesta usando coeficientes de reflexión.
3. ¿Qué impedancia de referencia del sistema vas a utilizar para resolver el problema?
4. Trace\(Z_{L}\) en el gráfico de Smith y etiquete el punto. (Recuerde usar normalización de impedancia si es necesario).
5. Trace\(Z_{G}\) en el gráfico de Smith y etiquete el punto.
6. Diseñe una red coincidente usando solo líneas de transmisión. Muestre su trabajo en la tabla de Smith. Debe expresar las longitudes de las líneas en términos de longitud eléctrica (ya sea grados o longitudes de onda). Se requieren impedancias características de las líneas. (Por lo tanto, tendrá un diseño que consiste en un trozo y otra longitud de línea de transmisión).

26. A continuación se muestra una red coincidente de dos puertos con un generador y una carga. La impedancia del generador es\(60\:\Omega\) y la impedancia de carga es\(Z_{L} = 30 + \jmath 30\:\Omega\). Utilice un gráfico de Smith para diseñar una red coincidente sin pérdidas. Es importante que se pueda seguir su solución, por lo que debe indicar su solución claramente en la tabla.

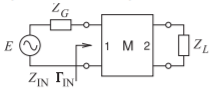
Figura\(\PageIndex{9}\)

1. ¿Cuál es la condición para la transferencia máxima de potencia desde el generador? Exprese su respuesta usando impedancias.
2. ¿Cuál es la condición para la transferencia máxima de potencia desde el generador? Exprese su respuesta usando coeficientes de reflexión.
3. ¿Qué impedancia de referencia del sistema vas a utilizar para resolver el problema?
4. Trace\(Z_{L}\) en el gráfico de Smith y etiquete el punto. (Recuerde usar normalización de impedancia si es necesario).
5. Trace\(Z_{G}\) en el gráfico de Smith y etiquete el punto.
6. Diseñe una red de coincidencia de elementos grumados sin pérdidas que muestre su proceso de diseño en el gráfico de Smith. Etiquetar puntos críticos en el gráfico de Smith. Dibuja la red coincidente y muestra los valores de reactancia.

27. A continuación se muestra una red coincidente de dos puertos con un generador y una carga. La impedancia del generador es\(30\:\Omega\) y la impedancia de carga es\(Z_{L} = 90 −\jmath 30\:\Omega\). Utilice un gráfico de Smith para diseñar una red coincidente sin pérdidas.

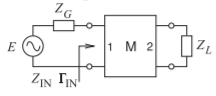
Figura\(\PageIndex{10}\)

1. ¿Cuál es la condición para la transferencia máxima de potencia desde el generador? Exprese su respuesta usando impedancias.
2. ¿Cuál es la condición para la transferencia máxima de potencia desde el generador? Exprese su respuesta usando coeficientes de reflexión.
3. ¿Qué impedancia de referencia del sistema vas a utilizar para resolver el problema?
4. Trace\(Z_{L}\) en el gráfico de Smith y etiquete el punto. (Recuerde usar normalización de impedancia si es necesario).
5. Trace\(Z_{G}\) en el gráfico de Smith y etiquete el punto.
6. Diseñe una red de correspondencia sin pérdidas que muestre su proceso de diseño en el gráfico de Smith. Etiquetar puntos críticos en el gráfico de Smith. Dibuja la red coincidente y muestra los valores de reactancia.

28. Utilice técnicas de gráfico Smith para diseñar una red de coincidencia de doble stub para hacer coincidir una carga con una admitancia normalizada\(y_{L} = 0.7−\jmath 5\) a una fuente con una admitancia normalizada de\(1\). Los stubs están cortocircuitados y están separados por una línea de transmisión de longitud\(\lambda /8\). La carga se encuentra en la posición del primer talón. Todas las líneas de transmisión tienen la impedancia característica del sistema. Su diseño debe dar la longitud de los dos talones.
    1. Trazar la carga en una gráfica de Smith. Indicar claramente la carga.
    2. Determinar las admisiones de cada uno de los talones. Muestre y describa claramente su técnica de diseño para que pueda ser entendida. Etiquete sus esfuerzos en una tabla de Smith y describa los pasos de diseño. Tenga en cuenta que se requiere una descripción y no simplemente marcas en un gráfico de Smith.
    3. Determine las longitudes eléctricas de los stubs (exprese su respuesta en términos de longitudes de onda o grados).
29. Utilice una línea de transmisión sin pérdidas y un elemento reactivo en serie para hacer coincidir una fuente con una impedancia equivalente a Thevenin de\(25 + \jmath 50\:\Omega\) a una carga de\(100\:\Omega\). (Es decir, use una línea de transmisión y una sola reactancia en serie).
    1. Dibuja la red coincidente con la fuente y carga.
    2. ¿Cuál es el valor de la reactancia en serie en la red coincidente (se puede dejar esto en ohmios)?
    3. ¿Cuál es la longitud y la impedancia característica de la línea de transmisión?
30. Considera una carga\(Z_{L} = 100 −\jmath 150\:\Omega\). Utilice el gráfico Smith para diseñar una red coincidente de dos stub que haga coincidir la carga con un\(50\:\Omega\) generador. Utilice las líneas de\(50\:\Omega\) transmisión en todas partes y asuma que la carga está inmediatamente al lado del primer trozo. Los dos talones están separados por una línea con una longitud eléctrica de\(45^{\circ}\). Ambos talones están cortocircuitados.
    1. Dibuja el sistema de stub correspondiente.
    2. ¿Cuál es la impedancia de carga normalizada?
    3. Indique brevemente el procedimiento utilizado para diseñar la red de coincidencia de dos stub. Necesitarás usar gráficos estilizados de Smith.
    4. Trazar la carga en una gráfica de Smith.
    5. ¿Cuál es la admisión del primer talón (Stub\(1\))?
    6. ¿Cuál es la longitud eléctrica de Stub\(1\)? (Tenga en cuenta que el talón está cortocircuitado).
    7. ¿Cuál es la admisión del segundo trozo cerca del generador (Stub\(2\))?
    8. ¿Cuál es la longitud eléctrica de Stub\(2\)? (Tenga en cuenta que el talón está cortocircuitado).
31. Considera una carga\(Z_{L} = 80 +\jmath 40\:\Omega\). Utilice el gráfico Smith para diseñar una red coincidente que consta de solo dos líneas de transmisión que coincidan con la carga a un generador de\(40\:\Omega\).
    1. Dibuja la red coincidente con líneas de transmisión. Si usa un talón, debe ser un talón cortocircuitado.
    2. Indique su elección de impedancia característica para sus líneas de transmisión. ¿Cuál es la impedancia de carga normalizada? ¿Cuál es la impedancia normalizada de la fuente?
    3. Resumir brevemente el procedimiento de diseño que va a utilizar. Deberá usar bocetos de gráficos Smith.
    4. Trazar la carga y la fuente en un gráfico de Smith.
    5. Completar el diseño de la red coincidente, proporcionando las longitudes de las líneas de transmisión.
32. A continuación se muestra una red coincidente de dos puertos con un generador y una carga. La impedancia del generador es\(40\:\Omega\) y la impedancia de carga es\(Z_{L} = 20 −\jmath 50\:\Omega\). Utilice un gráfico de Smith para diseñar la red coincidente.

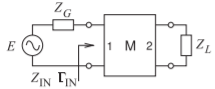
Figura\(\PageIndex{11}\)

1. ¿Cuál es la condición para la transferencia máxima de potencia desde el generador? Exprese su respuesta usando impedancias.
2. ¿Cuál es la condición para la transferencia máxima de potencia desde el generador? Exprese su respuesta usando coeficientes de reflexión.
3. ¿Qué impedancia de referencia del sistema vas a utilizar para resolver el problema?
4. Trace\(Z_{L}\) en una gráfica de Smith y etiquete el punto. (Recuerde usar normalización de impedancia si es necesario).
5. Trace\(Z_{G}\) en una gráfica de Smith y etiquete el punto.
6. Diseñe una red coincidente usando solo líneas de transmisión y muestre su trabajo en un gráfico de Smith. Debe expresar las longitudes de las líneas en términos de longitud eléctrica (ya sea grados o longitudes de onda largas). Se requieren impedancias características de las líneas. (Por lo tanto, tendrá un diseño que consiste en un trozo y otra longitud de línea de transmisión).

33. Utilice un gráfico Smith para diseñar una red de microcinta para hacer coincidir una carga\(Z_{L} = 10 −\jmath 30\:\Omega\) con una fuente\(Z_{S} = 60 +\jmath 40\:\Omega\). Utilizar un sustrato con permitividad\(\varepsilon_{r} = 10.0\) y espesor\(500\:\mu\text{m}\).
    1. ¿Cuál es la condición para la transferencia máxima de potencia?
    2. Desarrollar el diseño eléctrico de la red coincidente usando el gráfico Smith usando solo\(50\:\Omega\) líneas.
    3. Desarrollar el diseño físico completo de la red de emparejamiento. Dibuje el diseño de microcinta y etiquete las dimensiones críticas. Es decir, es necesario encontrar las dimensiones del circuito de microcinta.
34. Utilice una gráfica Smith para desarrollar el diseño eléctrico de una red de microcinta para hacer coincidir una carga\(Z_{L} = 25\:\Omega\) con una fuente\(Z_{S} = 250\:\Omega\). Utilice solo líneas\(50\:\Omega\) de transmisión. Utilice una línea de transmisión en serie y un trozo de circuito abierto. Debes usar un gráfico de Smith real y no un boceto de uno. Conteste las partes b, c y j-q, en una hoja separada de la tabla de Smith. Haz que tu trabajo sea fácil de seguir.
    1. Dibuje el problema de red coincidente etiquetando la red coincidente como\(\text{M}\).
    2. ¿Cuál es la condición para la transferencia de potencia máxima en términos de la impedancia de la fuente?
    3. ¿Cuál es la condición para la transferencia máxima de potencia en términos del coeficiente de reflexión de la fuente?
    4. Utilice una impedancia de\(50\:\Omega\) referencia y grafique las impedancias normalizadas de fuente y carga en una gráfica de Smith.
    5. Dibuje el lugar geométrico (a medida que aumenta la longitud de la línea) del coeficiente de reflexión mirando hacia una\(50\:\Omega\) línea terminada en la impedancia de la fuente.
    6. Dibuje el lugar del coeficiente de reflexión buscando en una\(50\:\Omega\) línea terminada en la impedancia de carga.
    7. Dibuje el lugar geométrico de una susceptancia de derivación en paralelo con la fuente (con la susceptancia de derivación variando en valor).
    8. Dibuje el lugar de una susceptancia de derivación en paralelo con la carga.
    9. De ahí identificar dos diseños de red coincidentes en el gráfico de Smith identificándolos como Diseño 1 y Diseño 2. Haga que la trayectoria de los diseños sea claramente visible, incluidas las direcciones, y etiquete las longitudes críticas y susceptancias en la tabla de Smith.
    10. Dibujar la topología de su Diseño 1 indicando los extremos de origen y carga y etiquetando las dimensiones críticas?
    11. ¿Cuál es la longitud de la línea de transmisión en serie en su Diseño 1?
    12. ¿Cuál es la entrada normalizada de entrada del stub en su Diseño 1?
    13. ¿Cuál es la longitud del talón de circuito abierto en tu Diseño 1?
    14. Dibuje la topología de su Diseño 2 indicando los extremos de origen y carga y etiquetando las dimensiones críticas?
    15. ¿Cuál es la longitud de la línea de transmisión en serie en su Design 2?
    16. ¿Cuál es la entrada normalizada de entrada del stub en su Diseño 2?
    17. ¿Cuál es la longitud del talón de circuito abierto en tu Design 2?
35. Repita el ejercicio 34 pero ahora con\(Z_{L} = 200\:\Omega\) y\(Z_{S} = 20\:\Omega\)).
36. Utilice un gráfico Smith para diseñar una red de microcinta para hacer coincidir una carga\(Z_{L} = 100 −\jmath 100\:\Omega\) con una fuente\(Z_{S} = 34 −\jmath 40\:\Omega\)). Utilice únicamente líneas de transmisión y no utilice stubs cortocircuitados. Utilice una impedancia de referencia de\(40\:\Omega\).
    1. Dibuje las impedancias de etiquetado de problemas de red coincidentes y la impedancia que busca en la red coincidente desde la fuente como\(Z_{1}\).
    2. ¿Cuál es la condición para la transferencia máxima de potencia en términos de impedancias?
    3. ¿Cuál es la condición para la transferencia máxima de potencia en términos de coeficientes de reflexión?
    4. Identificar, es decir, dibujar, al menos dos redes de coincidencia de microbandas adecuadas.
    5. Desarrollar el diseño eléctrico de la red coincidente usando el gráfico Smith usando solo\(40\:\Omega\) líneas. Solo necesitas hacer un diseño.
    6. Dibuje el diseño de microcinta de la red coincidente para identificar parámetros críticos tales como impedancias características y longitud eléctrica. Asegúrese de identificar cuál es el lado de origen y cuál es el lado de carga. No es necesario determinar los anchos de las mentiras ni sus longitudes físicas.
37. Repetir el ejercicio S10.31 pero ahora con\(Z_{L} = 10 −\jmath 40\:\Omega\) y\(Z_{S} = 28 −\jmath 28\:\Omega\)).
38. Utilice un gráfico de Smith para diseñar una red de coincidencia sin pérdidas de elementos agrupados de dos elementos para interconectar una fuente con una admisión\(Y_{S} = 6 −\jmath 12\text{ mS}\) a una carga con admitancia\(Y_{L} = 70 −\jmath 50\text{ mS}\).
39. Utilice un gráfico de Smith para diseñar una red coincidente sin pérdidas de elementos agrupados de dos elementos para interconectar una carga\(Z_{L} = 50 + \jmath 50\:\Omega\) con una fuente\(Z_{S} = 10\:\Omega\).

6.12.1 Ejercicios por Sección

\(†\)desafiante

\(§6.3\: 1, 2\)

\(§6.4\: 3, 4\)

\(§6.5\: 5, 6, 7, 8, 9, 10, 11†, 12†, 13†, 14†, 15†, 16†, 17†\)

\(§6.6\: 18†, 19†, 20†, 21†, 22†, 23†, 24†\)

\(§6.7\: 25†, 26†, 27†, 28†, 29†, 30†, 31†, 32†\)

\(§6.9\: 33†, 34, 35, 36, 37, 38, 39\)

6.12.2 Respuestas a ejercicios seleccionados

11. \(43.6-\jmath 106\:\Omega\)
12. (g) serie:\(\jmath 219\:\Omega\), derivación:\(-\jmath 225\:\Omega\)

16. b)\(200\)

19. c)\(Q=1.22467\)

22. \(C=1/(\omega_{d}^{2}L_{P})\)

25. d)\(1.25-\jmath 0.5\)

29. b)\(-\jmath 50\:\Omega\)

32. (f) línea\(40\:\Omega,\: 0.085\lambda\) larga antes de la carga, trozo corto\(40\:\Omega,\: 0.076\lambda\) largo