6.5: Manejo de cargas complejas

En esta sección se presentan estrategias para hacer frente a cargas complejas. En el enfoque de coincidencia algorítmica, el diseño procede primero ignorando la carga compleja y la fuente y luego contabilizándolos ya sea a través de la elección de la topología o cancelando su efecto a través de la resonancia.

6.5.1 Coincidencia

Las impedancias de entrada y salida de transistores, mezcladores, antenas, etc., contienen componentes resistivos y reactivos. Por lo tanto, un problema realista de adaptación de impedancia se parece al mostrado en la Figura 6.4.9. Los enfoques de coincidencia que se presentaron en las secciones anteriores se pueden aplicar directamente si\(X_{S}\) y\(X_{L}\) son tratados como reactancias parásitas que necesitan ser canceladas o, idealmente, utilizadas como parte de la red de emparejamiento. Existen dos enfoques básicos para manejar impedancias complejas:

1. Absorción: Absorba reactancias de fuente y carga en la propia red de adaptación de impedancia Esto se hace a través de la colocación cuidadosa de cada elemento coincidente de tal manera que los condensadores se colocan en paralelo con las capacitancias de fuente y carga, e inductores en serie con inductancias de fuente y carga. Los valores desviados se restan entonces de\(C\) los valores\(L\) y para la red coincidente calculados sobre la base de las partes resistivas de\(Z_{S}\) y\(Z_{L}\) solamente. Los nuevos valores (más pequeños),\(L'\) y\(C'\), constituyen los elementos de la red coincidente. En ocasiones es necesario realizar una conversión serie a paralelo, o paralelo a serie, de las impedancias de fuente o carga para que los elementos reactivos estén en la disposición correcta de serie o derivación para su absorción.
2. Resonancia: Resonan reactancias de fuente y carga con una reactancia igual y opuesta a la frecuencia de interés.

La presencia misma de una reactancia en una carga indica almacenamiento de energía y, por lo tanto, limitación de ancho de banda de algún tipo. En los enfoques anteriores para manejar una carga reactiva, el enfoque de resonancia podría resultar fácilmente en una solución de coincidencia de banda estrecha. El principal problema en el emparejamiento suele ser obtener suficiente ancho de banda. Lo que sea suficiente variará dependiendo de la aplicación. Para maximizar el ancho de banda, el objetivo general es minimizar el almacenamiento total de energía. En términos generales, la energía total almacenada será proporcional a la suma de las magnitudes de las reactancias en el circuito. Por supuesto, el almacenamiento de energía real depende de los niveles de voltaje y corriente, que a su vez variarán en el circuito. Un buen enfoque que conduce a grandes anchos de banda es incorporar la reactancia de carga en la red coincidente. Por lo tanto, la elección de la topología de red adecuada es crítica. Sin embargo, si el valor de reactancia de fuente y carga es mayor que el valor calculado del elemento de red coincidente, entonces no se puede usar la absorción por sí sola. En esta situación la resonancia debe combinarse con la absorción. En general, la mayoría de los diseños de adaptación de impedancia se basan en alguna combinación de resonancia y absorción.

Ejemplo\(\PageIndex{1}\): Matching Network Design Using Resonance

Para la configuración mostrada en la Figura\(\PageIndex{1}\), diseñe una red de adaptación de impedancia que bloqueará el flujo de corriente CC de la fuente a la carga. La frecuencia de operación es\(1\text{ GHz}\). Diseñar la red coincidente, descuidando la presencia de la\(10\text{ pF}\) capacitancia en la carga. Desde\(R_{S} = 50\:\Omega < R_{L} = 500\:\Omega\), y a partir de la Figura 6.4.2, considerar las topologías de las Figuras\(\PageIndex{2}\) (a) y\(\PageIndex{2}\) (b). El criterio de diseño de bloqueo del flujo de CC desde la fuente a la carga reduce la elección a la topología de la Figura\(\PageIndex{2}\) (b).

Solución

Paso 1:

\[\label{eq:1}|Q_{S}|=\left|\frac{X_{S}}{R_{S}}\right|=|Q_{P}|=\left|\frac{R_{L}}{X_{P}}\right|=\sqrt{\frac{R_{L}}{R_{S}}-1}=3\quad\text{and}\quad Q_{P}=\frac{R_{L}}{X_{P}} \]

Entonces\(X_{P} = \omega L = R_{L}/Q_{P} = 500/3\). Reduciendo esto da

\[\label{eq:2}\omega L=\frac{500}{3},\quad\text{and so}\quad L=\frac{500}{3\times 2\pi\times 10^{9}}=26.5\text{ nH} \]

Del mismo modo\(−X_{S}/R_{S} = 3\) y así

\[\label{eq:3}\frac{1/(\omega C)}{R_{S}}=3\quad\text{or}\quad C=\frac{1}{3\omega R_{S}}=\frac{1}{3\times 2\pi\times 10^{9}\times 50}=1.06\text{ pF} \]

Paso 2:

Resonar el\(10\text{ pF}\) condensador usando un inductor en paralelo:

\[\begin{align}\label{eq:4}(\omega L')^{-1}&=\omega\times 10\times 10^{-12} \\ \label{eq:5}L'&=\frac{1}{\omega ^{2}10^{-11}}=\frac{1}{(2\pi )^{2}10^{18}\times 10^{-11}}=2.533\text{ nH}\end{align} \]

Por lo tanto, la Figura\(\PageIndex{2}\) (c) es la red de correspondencia requerida. Dos inductores están en paralelo y el circuito se puede simplificar a lo que se muestra en la Figura\(\PageIndex{3}\), donde

\[\label{eq:6} L_{X}=(26.5\text{ nH}\parallel 2.533\text{ nH})=\frac{2.533\times 26.5}{2.533+26.5}\text{ nH}=2.312\text{ nH} \]

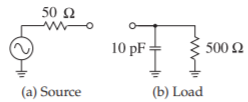
Figura\(\PageIndex{1}\): Problema de coincidencia considerado en Ejemplo\(\PageIndex{1}\).

Figura\(\PageIndex{2}\): Topología de red coincidente utilizada en Ejemplo\(\PageIndex{1}\): a) y (b) topología; y (c) red coincidente intermedia.

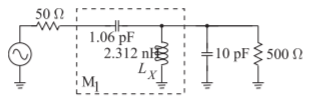
Figura\(\PageIndex{3}\): Red de coincidencia final en Ejemplo\(\PageIndex{1}\).

Ejemplo\(\PageIndex{2}\): Matching Network Design Using Resonance and Absorption

Para las configuraciones de fuente y carga que se muestran en la Figura\(\PageIndex{4}\), diseñe una red de adaptación de impedancia de paso bajo en\(f = 1\text{ GHz}\).

Solución

Ya que\(R_{S} < R_{L}\), utilice la topología que se muestra en la Figura\(\PageIndex{5}\) (a). Para una respuesta de paso bajo, la topología es la de la Figura\(\PageIndex{5}\) (b). Observe que la absorción es la forma natural de manejar el\(3\text{ nH}\) en la fuente y el\(5\text{ pF}\) en la carga. El proceso de diseño es el siguiente:

Paso 1:

Diseñar la red coincidente, descuidando los elementos reactivos en la fuente y carga:

\[\label{eq:7}|Q_{S}|=|Q_{P}|=\sqrt{\frac{R_{L}}{R_{S}}-1}=\sqrt{10-1}=3 \]

\[\begin{align}\label{eq:8}\frac{X_{S}}{R_{S}}&=3,\quad X_{S}=3\times 100,\quad \omega L=300\quad\text{and}\quad L=\frac{300}{2\pi\times 10^{9}}=47.75\text{ nH} \\ \label{eq:9}\frac{R_{P}}{X_{P}}&=-3\quad\text{and}\quad\frac{1000}{-(1/\omega C)}=-3\quad\text{and}\quad C=\frac{3}{1000\times 2\pi\times 10^{9}}=0.477\text{ pF}\end{align} \]

Este diseño se muestra en la Figura\(\PageIndex{6}\) (a). Esta es la red coincidente que hace coincidir la resistencia de la\(100\:\Omega\) fuente a la\(1000\:\Omega\) carga con las reactancias de origen y carga ignoradas.

Paso 2:

La Figura\(\PageIndex{6}\) (b) es la solución de emparejamiento provisional. La inductancia de la fuente se absorbe en la red coincidente, lo que reduce la inductancia en serie requerida de la red coincidente. La capacitancia de la carga no se puede absorber completamente. El diseño para el caso solo de resistencia requiere una capacitancia de derivación de\(0.477\text{ pF}\), pero\(5\text{ pF}\) está disponible a partir de la carga. Por lo tanto, hay un exceso de capacitancia de\(4.523\text{ pF}\) que debe ser resonado por la inductancia\(L''\):

\[\label{eq:10}\frac{1}{\omega L''}=\omega 4.523\times 10^{-12}.\quad\text{So}\quad L''=\frac{1}{(2\pi)^{2}\times 10^{18}\times 4.523\times 10^{-12}}=5.600\text{ nH} \]

El diseño final de la red de adaptación\(\PageIndex{6}\) (Figura (c)) absorbe completamente la inductancia de la fuente en la red coincidente, pero solo absorbe parcialmente la capacitancia de carga.

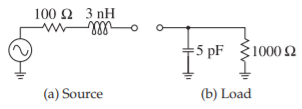
Figura\(\PageIndex{4}\): Problema de coincidencia en Ejemplo\(\PageIndex{2}\).

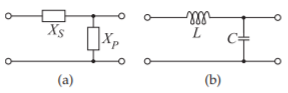
Figura\(\PageIndex{5}\): Topologías a las que se hace referencia en el Ejemplo\(\PageIndex{2}\).

Figura\(\PageIndex{6}\): Evolución de la red coincidente en Ejemplo\(\PageIndex{2}\): (a) diseño de red coincidente considerando solo las resistencias de origen y carga; (b) red coincidente con las partes reactivas de la fuente y las impedancias de carga incluidas; y (c) diseño final.