1.6: Leyes de Campo Eléctrico y Magnético

Antes de que se postularan las ecuaciones de Maxwell, se conocían varias leyes de la electromagnetica. Estas son la ley Biot—Savart, la ley circuital de Ampere, la ley de Gauss, la ley de Gauss para el magnetismo y la ley de Faraday. Las leyes son para circunstancias específicas y principalmente para campos estáticos. En esta sección están

1.6.1 Ley Circuital de Ampere

La ley circuital de Ampere, a menudo llamada solo ley de Ampere, relaciona la corriente continua y el campo magnético estático\(\overline{H}\). La relación se basa en la Figura\(\PageIndex{1}\). En la situación estática,\(\partial \overline{D}/\partial t= 0\), y así una de las ecuaciones de Maxwell, la ecuación (1.5.36), reduce a

\[\label{eq:1}\oint_{\ell}\overline{H}\cdot d\ell =I_{\text{enclosed}} \]

Esta es la ley circuital de Ampere.

1.6.2 Ley Biot-Savart

La ley Biot-Savart relaciona la corriente con el campo magnético estático. Con\(\partial\mathbf{D}/\partial t = 0\), la ecuación (1.5.3) se convierte

\[\label{eq:2}\nabla\times\overline{H}=\overline{J} \]

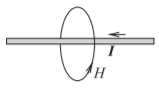
Figura\(\PageIndex{1}\): Diagrama que ilustra la ley de Ampere. La ley de Ampere relaciona la corriente en un cable con el campo magnético que lo rodea.

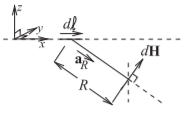
Figura\(\PageIndex{2}\): Diagrama que ilustra la ley Biot-Savart. La ley Biot-Savart relaciona la corriente con el campo magnético.

En las coordenadas cartesianas,

\[\label{eq:3}\nabla\times\overline{H}=\left(\frac{\partial H_{z}}{\partial y}-\frac{\partial H_{y}}{\partial z}\right)\hat{\mathbf{x}} +\left(\frac{\partial H_{x}}{\partial z}-\frac{\partial H_{z}}{\partial x}\right)\hat{\mathbf{y}}+\left(\frac{\partial H_{y}}{\partial x}-\frac{\partial H_{x}}{\partial y}\right)\hat{\mathbf{z}} \]

y si la corriente se limita a un cable delgado como se muestra en la Figura\(\PageIndex{2}\), se\(\nabla\times\overline{H}\) reduce a una operación a lo largo del cable, pero también con información vectorial. Así que el primer paso en el desarrollo de la ley Biot—Savart, Ecuación\(\eqref{eq:2}\), se simplifica a (ignorando la información vectorial por ahora)

\[\label{eq:4}\frac{\partial H}{\partial\ell}=\frac{I}{4\pi R^{2}} \]

Con información vectorial y moviendo la longitud infinitesimal del alambre\(d\ell\), desde el lado izquierdo de la ecuación hacia la derecha, se obtiene la forma final de la ley Biot—Savart:

\[\label{eq:5}d\overline{H}=\frac{Id\ell\times\hat{\mathbf{a}}_{R}}{4\pi R^{2}} \]

que tiene las unidades de amperios por metro en el sistema SI. En Ecuación\(\eqref{eq:5}\),\(I\) es corriente,\(d\ell\) es un incremento de longitud de un filamento de corriente\(I\),\(\hat{\mathbf{a}}_{R}\) es el vector unitario en la dirección del filamento de corriente al campo magnético, y\(R\) es la distancia entre el filamento y el incremento del campo magnético. Entonces Ecuación\(\eqref{eq:5}\) está diciendo que un filamento de corriente produce un campo magnético en un punto. El campo magnético estático total de una corriente en un alambre o superficie se puede encontrar modelando el alambre o superficie como una serie de filamentos de corriente, y el campo magnético total en un punto se obtiene resumiendo las contribuciones de cada filamento.

1.6.3 Ley de Gauss

La tercera ley es la ley de Gauss, que relaciona el vector de densidad de flujo eléctrico estático\(\mathbf{D}\),, a cargar. Con referencia a la Figura\(\PageIndex{3}\), la ley de Gauss en forma integral es

\[\label{eq:6}\oint_{s}\overline{D}=\int_{v}\rho_{v} dv=Q_{\text{enclosed}} \]

que establece que la integral del vector de densidad de flujo eléctrico,\(\overline{D}\), es igual a la carga total encerrada por la superficie,\(Q_{\text{enclosed}}\). Esta es solo la forma integral de la tercera ecuación de Maxwell (Ecuación (1.5.37)).

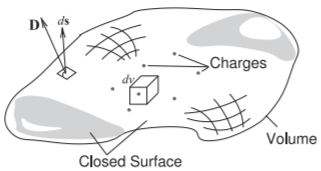
Figura\(\PageIndex{3}\): Diagrama que ilustra la ley de Gauss. Las cargas se distribuyen en el volumen encerrado por la superficie cerrada. Un área incremental es descrita por el vector\(d\mathbf{s}\) que es normal a la superficie y cuya magnitud es el área del área incremental.

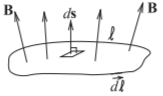
Figura\(\PageIndex{4}\): Diagrama que ilustra la ley de Faraday. El contorno\(\ell\) encierra la superficie.

Existe una ley similar llamada ley de Coulomb que dice que la magnitud de la fuerza entre dos cargas puntuales estacionarias es directamente proporcional al producto de las magnitudes de cargas e inversamente proporcional al cuadrado de la distancia entre ellas. Esta ley puede derivarse de la ley de Gauss pero es menos general. La ley de Coulomb se aplica únicamente a los cargos estacionarios mientras que con la ley de Gauss los cargos pueden estar moviéndose.

La ley de Gauss también se ha utilizado para el campo magnético donde se llama la ley de Gauss para el magnetismo. En forma integral, la ley de Gauss para el magnetismo es

\[\label{eq:7}\oint_{s}\overline{B}=0 \]

donde\(\overline{B}\), es la densidad de flujo magnético estático. Esta ley es lo mismo que decir que no hay cargas magnéticas. “La ley de Gauss para el magnetismo” es un nombre que no se usa universalmente y mucha gente simplemente dice que no hay cargas magnéticas.

1.6.4 Ley de Faraday

La ley de Faraday relaciona un campo magnético variable en el tiempo con una caída de voltaje inducida\(V\), que ahora se entiende como\(\oint_{\ell}E\cdot d\ell\), es decir, la integral de contorno cerrado del campo eléctrico,

\[\label{eq:8}V=\oint_{\ell}\overline{\mathcal{E}}\cdot d\ell =-\oint_{s}\frac{\partial\overline{\mathcal{B}}}{\partial t}\cdot d\mathbf{s} \]

y esto tiene las unidades de voltios en el sistema de unidades SI. Esta es solo la primera de las ecuaciones de Maxwell en forma integral (ver Ecuación (1.5.35)). La operación descrita en la Ecuación\(\eqref{eq:8}\) se ilustra en la Figura\(\PageIndex{4}\).